
- •II. Дифференциальное исчисление функций нескольких переменных
- •§ 1. Функции нескольких переменных. Основные понятия.
- •Область существования. Линии и поверхности уровня
- •§ 2. Предел и непрерывность функции нескольких переменных
- •§ 3. Частные производные и полный дифференциал функции нескольких переменных
- •Пример 3.3. Найти полный дифференциал функции в точке .
- •§ 4. Производная сложной функции
- •§ 5. Производная по направлению. Градиент
- •Пример 5.1. Для функции найти градиент и производную по направлению векторав точке.
- •§ 6. Дифференцирование неявных функций
- •§ 7. Замена переменных
- •§ 8. Геометрические приложения
- •§ 9. Формула Тейлора и ряд Тейлора
- •§ 10. Экстремум функции нескольких переменных
Пример 3.3. Найти полный дифференциал функции в точке .
Решение. Найдем частные производные заданной функции:
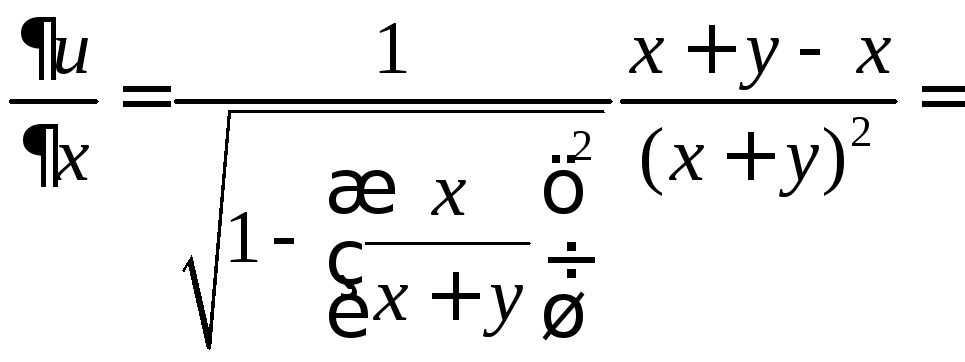
 ,
,
 .
.
Полный дифференциал
функции
 .
.
Тогда

 .
.
Значение дифференциала
в точке
![]() равно
равно  .
.
Пример 3.4.
Дана функция
![]() .
Проверить, является ли она решением
уравнения
.
Проверить, является ли она решением
уравнения
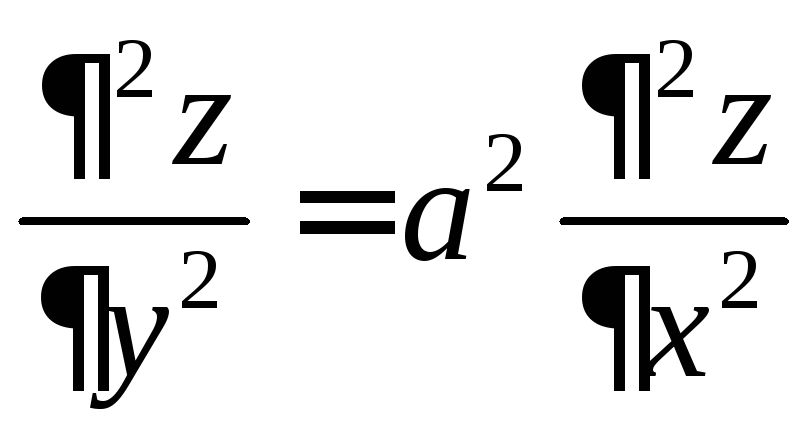 .
.
Решение. Найдем последовательно частные производные первого и второго порядка:
 ;
;
 .
.
После подстановки этих производных в уравнение получим
![]()
![]() ,
,
т. е.
![]() является решением уравнения.
является решением уравнения.
Пример 3.5.
Дана функция
![]() .
Показать, что
.
Показать, что
![]()
 .
.
Решение. Найдем частные производные первого и второго порядка заданной функции:
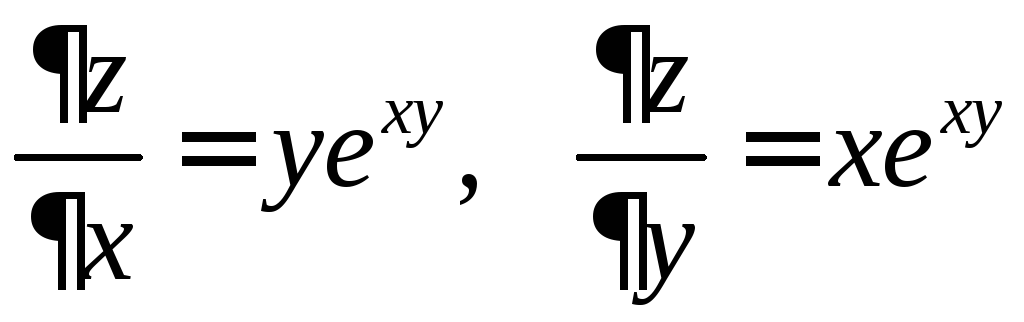 ;
;
 ;
;
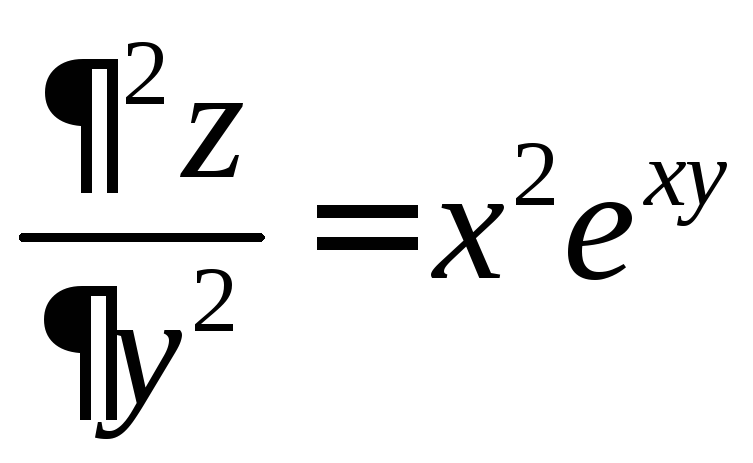 ;
;
 .
.
Подставим найденные
производные в выражение для
![]() :
:

что и требовалось показать.
Пример 3.6.
Найти дифференциал
второго порядка функции
![]() .
.
Решение. Дифференциал второго порядка определим с помощью формулы
 .
.
Воспользуемся полученными в примере 3.5 производными второго порядка.
Тогда
![]() ,
,
или
![]() .
.
Пример 3.7.
Вычислить
приближенно
![]() .
.
Решение.
Положим
![]()
Тогда
![]() .
Вычислим частные производные функции
в точке с координатами
.
Вычислим частные производные функции
в точке с координатами![]() :
:
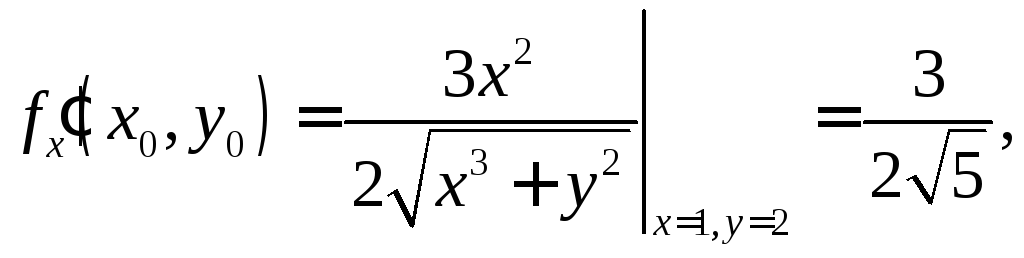
 .
.
Подставив полученные данные в формулу приближенных вычислений, получим, что
 .
.
3.1.
Найти
![]() и
и![]() ,
если
,
если![]() .
Является ли эта функция дифференцируемой
в точке
.
Является ли эта функция дифференцируемой
в точке
![]() ?
?
Найти частные производные первого и второго порядка от следующих функций:
|
3.2.
|
3.3.
|
|
3.4.
|
3.5.
|
|
3.6.
|
3.7.
|
3.8.
Проверить равенство
 ,
если:
,
если:
|
а)
|
б)
|
3.9.
Пусть
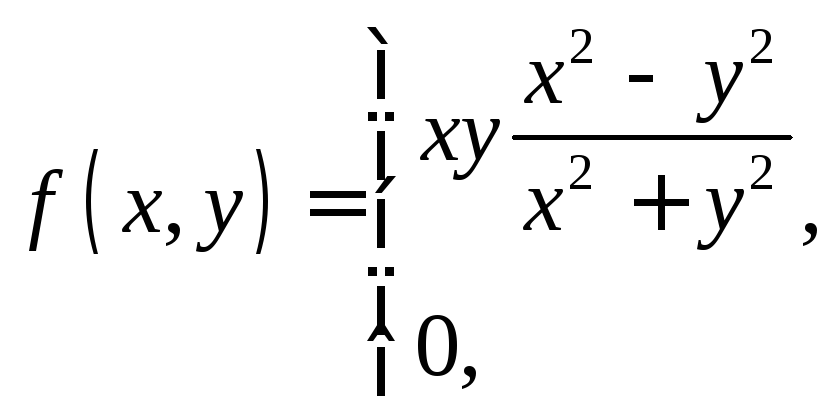

Показать, что
![]() .
.
3.10.
Пусть
![]() – дважды дифференцируемая однородная
функция измерения
– дважды дифференцируемая однородная
функция измерения![]() .
Доказать, что
.
Доказать, что
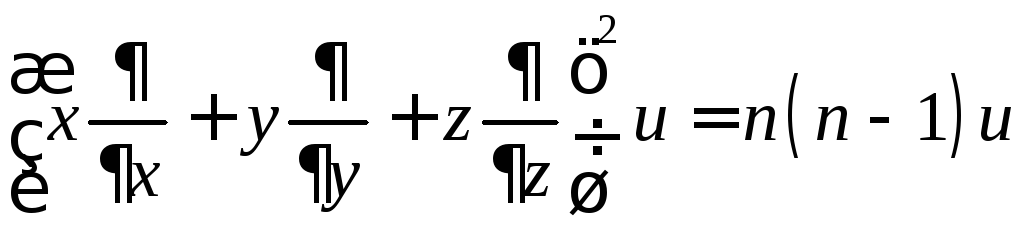 .
.
Найти дифференциалы первого и второго порядков от следующих функций:
|
3.11.
|
3.12.
|
|
3.13.
|
|
Заменив приращение функции дифференциалом, приближенно вычислить:
|
3.14.
а)
|
б)
|
|
в)
|
|
Найти частные производные:
|
3.15.
|
|
![]() .
.
3.16.
 если
если![]() .
.
3.17.
 если
если![]() .
.
Найти дифференциалы указанного порядка:
|
3.18.
|
3.19.
|
3.20.
Пусть
 .
Найти
.
Найти![]() ,
если:
,
если:
|
а)
|
б)
|
Ответы: 3.1.
![]() ,
,![]() .
Функция недифференцируема в точке.3.14. а)
108,972, б) 2,95б в) 0,502. 3.15.
.
Функция недифференцируема в точке.3.14. а)
108,972, б) 2,95б в) 0,502. 3.15.  ,
, .
3.16.
.
3.16.  . 3.17.
. 3.17.  .
.
3.18.  .
3.19.
.
3.19. ![]() .
.
3.20. а) ![]() ,
б)
,
б)![]() .
.
§ 4. Производная сложной функции
Производную сложной функции рассмотрим на примере функции двух переменных.
Пусть на множестве
![]() определена сложная функция
определена сложная функция![]() ,
где
,
где![]() ,
,![]() ,
и пусть функции
,
и пусть функции![]() ,
,![]() имеют в некоторой окрестности точки
имеют в некоторой окрестности точки![]() непрерывные частные производные, а
функция
непрерывные частные производные, а
функция![]() имеет непрерывные частные производные
в некоторой окрестности точки
имеет непрерывные частные производные
в некоторой окрестности точки![]() ,
где
,
где![]() ,
,![]() .
Тогда сложная функция
.
Тогда сложная функция![]() дифференцируема в точке
дифференцируема в точке![]() и её частные производные вычисляются
по следующим формулам:
и её частные производные вычисляются
по следующим формулам:

В частности, если
функция
![]() является функцией двух переменных,
которые в свою очередь есть функции
одной переменной
является функцией двух переменных,
которые в свою очередь есть функции
одной переменной![]() ,
,![]() ,
то производная вычисляется по формуле
,
то производная вычисляется по формуле
![]() .
.
Пример 4.1.
Найти частные производные функции ![]() ,
где
,
где
![]() .
.
Решение. Имеем
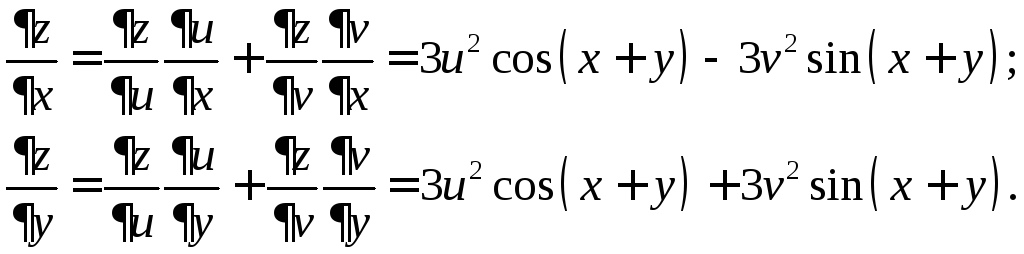
Пример 4.2.
Найти производные
![]() и
и![]() функции
функции![]() ,
где
,
где ,
, .
.
Решение. Используем правило дифференцирования сложной функции:
![]() ,
,
 .
.
Найдем все частные производные, входящие в данные равенства:


 .
.
Тогда частные
производные сложной функции
![]() запишутся следующим образом:
запишутся следующим образом:
 ;
;
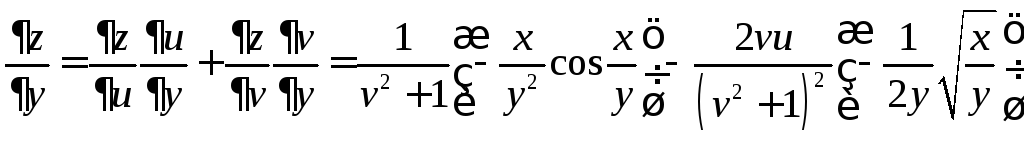 .
.
Подставив функции
 и
и в найденные выражения, окончательно
получим:
в найденные выражения, окончательно
получим:
 ;
;
 .
.
Доказать, что если
![]() – произвольная дифференцируемая
функция, то функция
– произвольная дифференцируемая
функция, то функция![]() удовлетворяет следующему уравнению:
удовлетворяет следующему уравнению:
4.1.
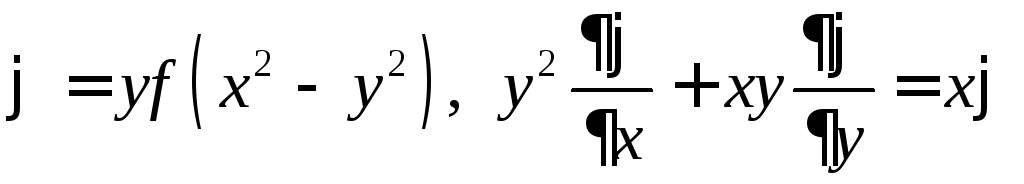 .
.
4.2.
 .
.
4.3.
 .
.
Найти производные первого и второго порядков от следующих сложных функций:
|
4.4.
|
4.5.
|
Найти полные дифференциалы первого и второго порядков от следующих сложных функций:
|
4.6.
|
4.7.
|
|
4.8.
|
|
4.9.
![]() ,
где
,
где![]() .
.
Найти
![]() ,
если:
,
если:
|
4.10.
|
4.11.
|
4.12.
Показать, что функция
![]() (
(![]() и
и![]() – постоянные) удовлетворяет уравнению
Лапласа
– постоянные) удовлетворяет уравнению
Лапласа
 .
.
4.13.
Показать, что
функция
 (
(![]() и
и![]() – постоянные) удовлетворяет уравнению
теплопроводности
– постоянные) удовлетворяет уравнению
теплопроводности
 .
.
4.14.
Упростить выражение
 ,
если
,
если
![]() ,
где
,
где
![]() – дифференцируемая функция.
– дифференцируемая функция.
4.15. Пусть
![]()
и
![]() .
.
Доказать, что
![]() .
.
Предположив, что
произвольные функции
![]() дифференцируемы достаточное число раз,
проверить следующие равенства:
дифференцируемы достаточное число раз,
проверить следующие равенства:
4.16.
 ,
если
,
если .
.
4.17.
 ,
если
,
если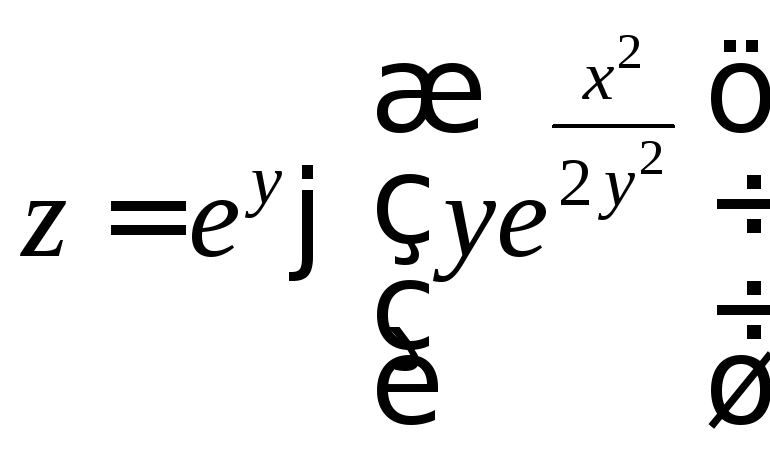 .
.
4.18.
 ,
если
,
если .
.
Ответы: 4.4.
![]() ;
; ;
;
 ;
;
 ;
;
 .
.
4.6.
![]() ,
,![]() . 4.7.
. 4.7. ![]() ,
,
![]() .
4.10.
.
4.10. ![]() .4.14.
.4.14.
![]() .
.

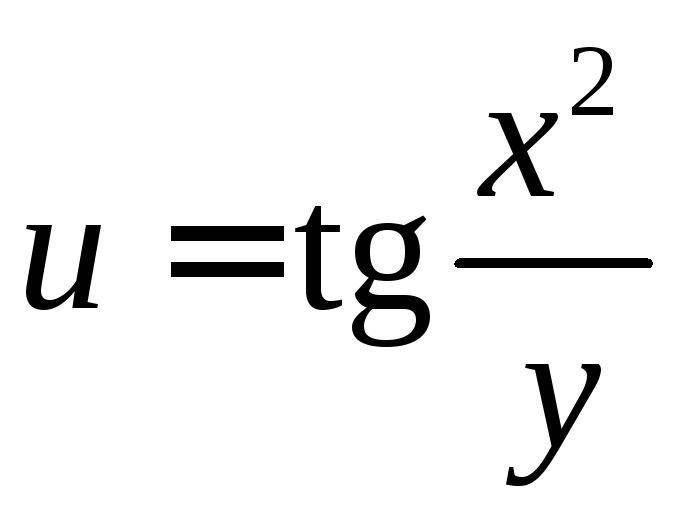 .
. .
. .
. .
. если
если