2.Исследование кривой второго порядка

2.1 Определение зависимости типа кривой от параметра с помощью инвариантов

Для уравнения данной кривой второго порядка

(2.1)

имеем:

Вычислим инварианты кривой по формулам:

Узнаем как изменяются инварианты в зависимости от β:

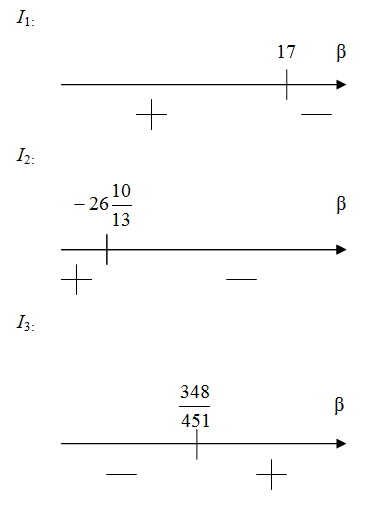
Зная как изменяются инварианты в зависимости от β можно составить таблицу, в которой отображаются знаки всех инвариантов:

β	(-∞; )		( ; )		( ;17)	17	(17;+∞)
I1	+	+	+	+	+	0	-
I2	+	0	-	-	-	-	-
I3	-	-	-	0	+	+	+

Используя эту таблицу можно, в соответствии с классификацией кривых второго порядка, узнать как изменяется кривая в зависимости от β:

1. При , I2>0 , I1 I3<0 , следовательно при данных значениях β кривая является эллипсом. (Рис. 1)

2. При , I2=0 , I3≠0 , следовательно при данном значении β кривая является параболой. (Рис. 2)

3. При ( ; ) , I2<0 , I3≠0 , следовательно при данных значениях β кривая является гиперболой. (Рис. 3)

4. При , I2<0 , I3=0 , следовательно при данном значении β кривая является двумя пересекающимися прямыми. (Рис. 4)

5. При , I2<0 , I3≠0 , следовательно при данных значениях β кривая является гиперболой. (Рис. 5)

Используя полученные результаты, построим таблицу зависимости типа кривой от значения параметра β.

Значение параметра	(-∞; )		( ; )
Тип кривой	Эллипс	Парабола	Гипербола	Две пересекающиеся прямые	Гипербола

Кривая поверхность порядок

2.2 Построение кривых при различных значениях параметра

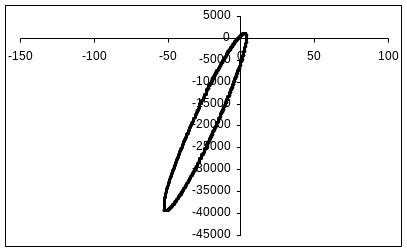
Рис. 1. Кривая при Рис. 2. Кривая при

Рис. 3. Кривая при Рис. 4. Кривая при

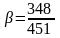
Рис. 5. Кривая при

2.3 Приведение уравнения кривой при β = 0 к каноническому виду

(2.2)

Для уравнения кривой второго порядка (2.1) имеем:

Из таблицы зависимости типа кривой от значения параметра β видно , что при β=0 кривая второго порядка является гиперболой.

Совершим параллельный перенос начала координат в точку При этом координаты x, y произвольной точки M плоскости в системе координат xOy и координаты x', y' в новой системе координат x'O'y' связаны соотношениями

(2.3)

Подставляя выражения (2.3) в уравнение (2.2), получим:

Раскрывая скобки и приводя подобные члены, получим:

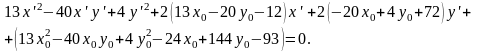(2.4)

В уравнении (2.4) коэффициенты при x' и y' приравняем нулю. Получим систему уравнений относительно x0, y0

которая определяет координаты центра исходной кривой. Т.к. x0 =4, y0 = 2 — решение данной системы, то точка O'(4, 2) — центр данной кривой. Подставим найденные значения x0, y0 в уравнение (2.4). В новой системе координат x'O'y' в уравнении (2.4) коэффициенты при x' и y' равны нулю и уравнение примет вид

(2.5)

Так как 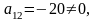то дальнейшее упрощение уравнения (2.5) достигается при помощи поворота осей координат на угол . При повороте осей координат на угол координаты x', y' произвольной точки M плоскости в системе координат x'O'y' и координаты X, Y в новой системе координат XO'Y связаны соотношениями

(2.6)

Подставляя (2.6) в уравнение кривой (2.5), получим

Раскроем скобки:

Приводя подобные члены, получим уравнение

(2.7)

Выберем такой угол , что в уравнении (2.7) коэффициент при произведении XY равен нулю:

(2.8)

Разделим правую и левую части уравнения (2.8) почленно на . Мы можем это сделать, так как , потому что если (то есть ), то при подстановке в уравнение (2.8) получим, что и , что противоречит основному тригонометрическому тождеству . Получим уравнение

(2.9)

Решая уравнение (2.9), получим

Выберем 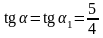Получим:

Подставляя эти значения в уравнение (2.7), получим:

соответственно, уравнение :

— это каноническое уравнение исходной гиперболы (см. рис. 6).

2.4 Определение эксцентриситета, фокусов, директрис, асимптот данной кривой второго порядка

1. Найдем фокусы. Для того чтобы найти фокусы гиперболы воспользуемся следующими формулами: F1(–c, 0), F2(c, 0), где

Следовательно, фокусы имеют вид:

2. Найдем эксцентриситет. Эксцентриситетом гиперболы называется величина

3. Найдем директрисы:

4. Найдем асимптоты по формуле:

2.5 Построение кривой второго порядка в общей и канонической системах координат

Рис.6. Кривая в канонической системе координат

Рис.7. Кривая в общей системе координат

3.Общая теория поверхностей второго порядка

3.1 Поверхности второго порядка

Поверхностью второго порядка S называется геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида:

(3.1)

где, по крайней мере, один из коэффициентов отличен от нуля.

Уравнение (4.1) называют общим уравнением поверхности второго порядка S, а систему координат Oxyz называют общей системой координат.

Теорема: Для произвольной поверхности S, заданной общим уравнением (3.1), существует такая декартова прямоугольная система координат O'XYZ что в этой системе поверхность S задана уравнением одного из следующих канонических видов:

1) — эллипсоид,

2) 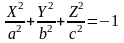— мнимый эллипсоид,

3) — однополостный гиперболоид,

4) — двуполостный гиперболоид,

5) — конус,

6) — мнимый конус (точка),

7) 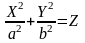— эллиптический параболоид,

8) — гиперболический параболоид,

9) — эллиптический цилиндр,

10) — мнимый эллиптический цилиндр,

11) — две мнимые пересекающиеся плоскости (ось O'Z),

12) — гиперболический цилиндр,

13) — две пересекающиеся плоскости,

14) — параболический цилиндр,

15) — две параллельные плоскости,

16) 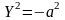— две мнимые параллельные плоскости,

17) — две совпадающие плоскости (плоскость XOZ).

В вышеперечисленных уравнениях a, b, c, p — положительные параметры. Систему координат O'XYZ называют канонической.