50. Выпуклое программирование.

Общая постановка задачи. (min/max) (1)

при условии 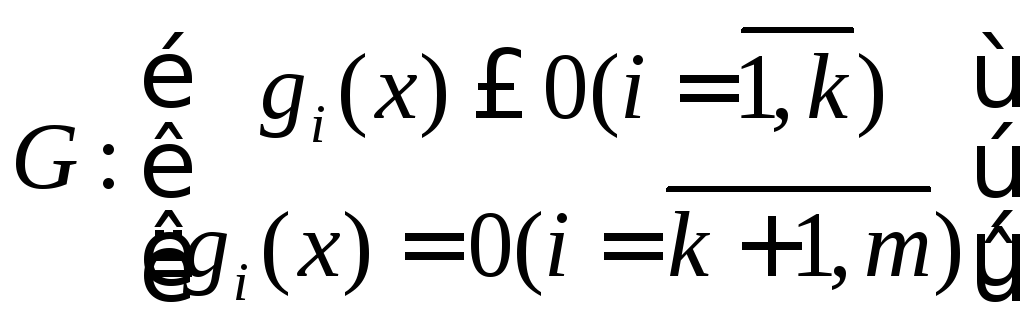(2)

где (n-мерный вектор)

Задача мат. программирования в которой среди функций f(x) и нелинейные функции называется ЗНЛП (задачей нелинейного программирования).Задача (1)-(2) называется задачей выпуклого программирования, если f(x) является выпуклой(вогнутой) и выпуклые. f(x) - целевая функция, а система (2) – система ограничений. Система (2) может также содержать и условие неотрицательности вектора x, или неравенство противоположного знака. Если система (2) отсутствует а f(x) не линейна, то получаем задачу НЛП без ограничений. Если присутствует хотя бы одно ограничение то имеем задачу НЛП с ограничениями, причем множество дополнительных решений определяется этой системой. Множество допустимых решений задачи (1)-(2) удовлетворяет условию регулярности если хотя бы одна точка , для которой выполняется неравенство . Th: Любой локальный max(min) в ЗВП соотв явл глоб max(min). В ЗВП можно составить ф-ю Лагранжа вида L(x1,..,xn,y1,..,yn)=f(x1,..,xn)+(i=1,m)yi(bi-gi(x1,..,xn)), где yi (i=,m) –мн-н Лагранжа. т(x⁰,y⁰)=(x1⁰,..,xn⁰,y1⁰,..,ym⁰) наз седл т фи Лагранжа, если имеет место нер-во L(x1,..,xn,y1⁰,..,ym⁰)<=L(x1⁰,..,xn⁰)<=L(x1⁰,..,xn⁰,y1,..,ym).

2) Различные формы условий оптимальности.

А)Координатная форма.

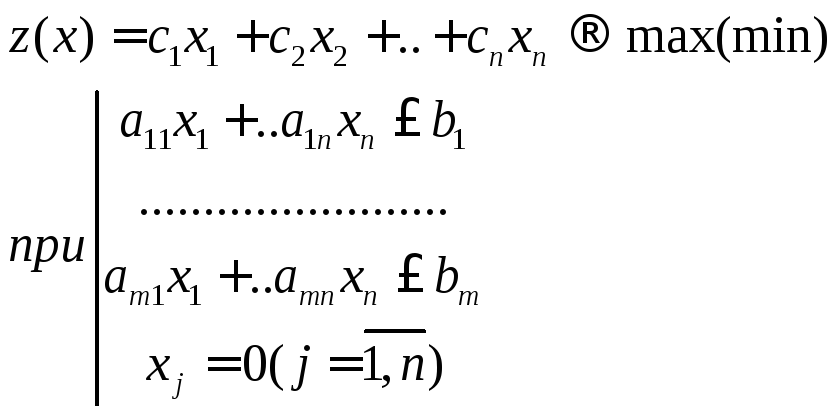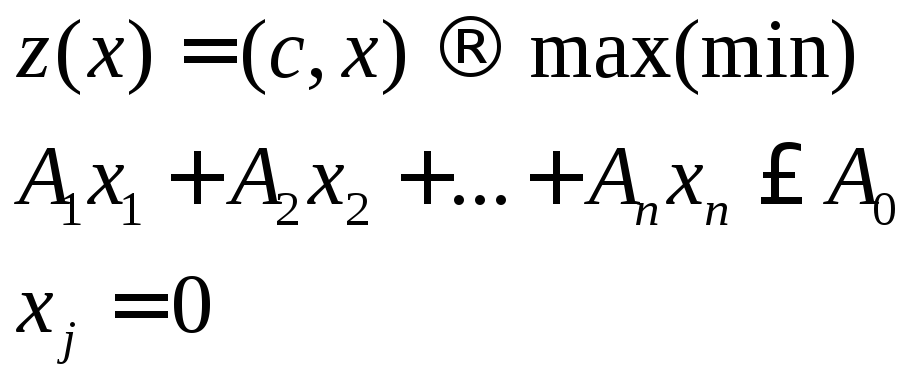Б)Векторная формагде -вектор координат целевой функции где - вектор условий системы ограничений где

В) Матричная форма 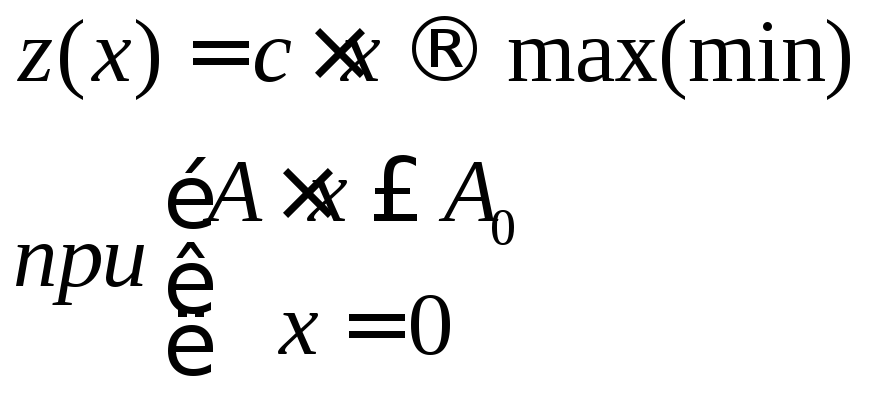где С-матрица,

Графический метод решения задач нелинейного программирования для функций 2 переменных.Рассмотрим ЗНЛП с линейными ограничениями и нелинейной целевой функцией. Если число переменных равно 2, то область допустимых решений можно изобразить на плоскости, в противном случае нужно проверить, выполняется ли условие n-m=2 и разрешить исходную систему относительно части переменных, выразить переменные через 2 переменные, в результате получим систему ограничений и целевую функцию, зависящие от 2 переменных. Сист ограничений задает ОДР, а поведение целевой функции можно охарактеризовать с помощью линии уровня. Для целевой функции требуется определить градиент (вектор скорейшего роста функции). При перемещении линии уровня по направлению вектора нормали до граничной точки области G будем получать опорные линии. Нужно найти самую удаленную – она будет max, (min - аналогично)при этом т min/max могут лежать в G или на границе G или быть угловыми точками. Теорема Куна-Таккера.Для задачи (min/max) (1) при условии G: [g_i(x1,..,xn)<=bi (i=1,m); xi>=0 (i=1,n)](2) допустимое множество решений, удовлетворяющих условию регулярности, точка является оптимальным решением т. и т. т. к. вектор , такой, что является Седловой точкой ф-ции Лагранжа. - оптимальное решение задачи. (Опр. Точка называется седловой точкой функции Лагранжа, если имеет место неравенство при ) Опр. Ф-цией Лагранжа ЗВП называется функция вида где Принципы построения методов оптимизации, соответствующие им конкретные алгоритмы, сходимость алгоритмов.Принцип решения задач.1)Составить функцию Лагранжа 2)Записать н. и д. условия существования Седловой точки функции Лагранжа 3)Найти седловую точку или установить ее отсутствие 4)Записать оптимальное решение исходной задачи и найти значение целевой функции.Конкретный алгоритм решения задач – метод штрафных функций.Рассм. ЗНЛП где f(x) – нелинейная функция (1) при условии G: [g_i(x1,..,xn)<=0 (i=1,m); xi>=0 (i=1,n)] (2) Эту задачу на условный экстремум можно свести к задаче на безусловный экстремум путем видоизменения целевой функции. В соотв-и с МШФ составляется новая целевая функция, которая строится из исходной целевой функции и специальной функции штрафа. Идея метода состоит в построении и исследовании последовательностей новых целевых функций, имеющих вид: , где k=1,2,… , где - функция штрафа, которая принимает очень малье, фактически нулевые значения внутри ОДР, и значение которой резко увеличивается по мере удаления от ОДР. -возрастающая последовательность натуральных чисел, которая называется параметром штрафа. Функцию штрафа можно задать т. н. срезкой функций: =(i=1,m)[g_i+(x)]² (т.е. сумма квадратов срезок функций . задается так

Алгоритм решения методом штрафных функций 1)Выбирается приближенное начальное значение и монотонно возрастающая последовательность чисел r_k2)Для n=1,2,…, начиная с точки составляется и решается задача нахождения безусловного экстремума вспомогательных функций , в результате чего находится очередное приближение 3) Каждый раз при построении делаются предположения о срезках функции . Исследовании продолжаются до тех пор, пока выдвинутое положение не подтвердится.