Простейшие типы точек покоя. Автономные динамические системы двух уравнений первого порядка. Типы особых точек на фазовой плоскости

.

1. – это автономная система, т. к. правая часть от времени не зависит.

- решение системы (1)

Точку (a₁,…,a_n) фазового пространства (x₁,…,x_n) будем называть точкой покоя (точкой положения равновесия) системы. (особая точка)

Точка x_i=0 – точка покоя.

Пусть S(R) – шар

Опр. Будем говорить, что точка покоя x₁=0,…,x_n=0 системы (1) устойчива, если для такая чтотраектория системы, начинающаяся в момент времени t=t₀ в точке , все время остается в шаре .

Точка покоя асимптотически устойчива, если:

1. она устойчива;

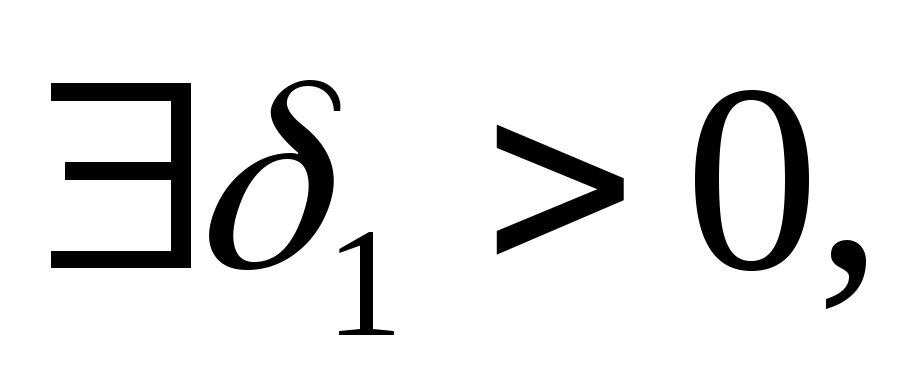2. что каждая траектория системы, начинающаяся в точке 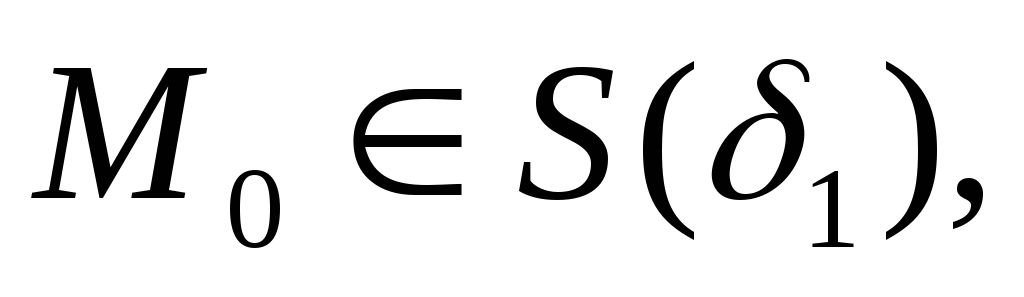стремится к началу координат, когда время неограниченно растет.

Пример 1:

С течением времени точки приближаются к началу координат. => точки покоя асимптотически устойчивы.

Исследуем расположение траектории в окрестности точки покоя x=0, y=0 системы двух линейных однородных уравнений с постоянными коэффициентами:

Предполагается, что определитель 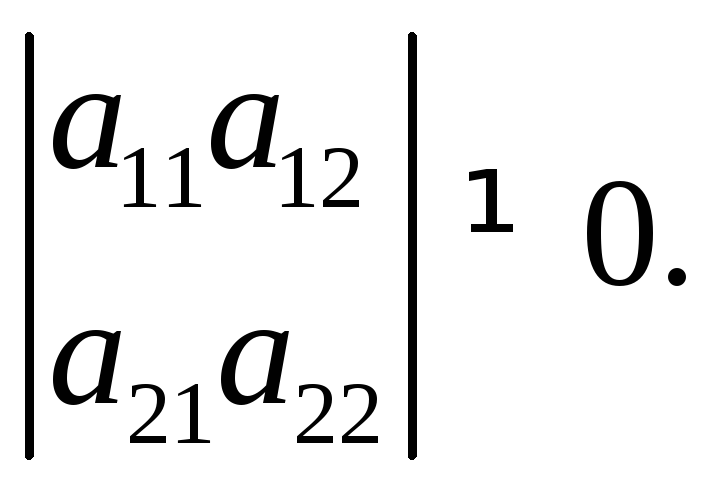(0, 0) – точка покоя.

Решение системы (2) будем искать в виде:

После нахождения λ из характеристического уравнения (3), величины α и β находятся из системы (*) с точностью до постоянного множителя.

Возможные случаи:

А) Корни λ₁, λ₂ характеристического уравнения (3) действительные и различные. Общее решение системы (2) имеет вид:

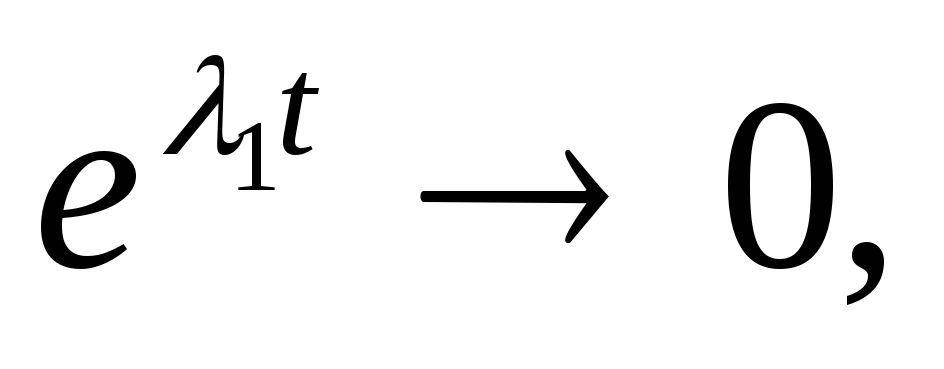
1. Пусть λ₁<0, λ₂<0.Точка покоя (0;0) в этом случае асимптотически устойчива, т.к. 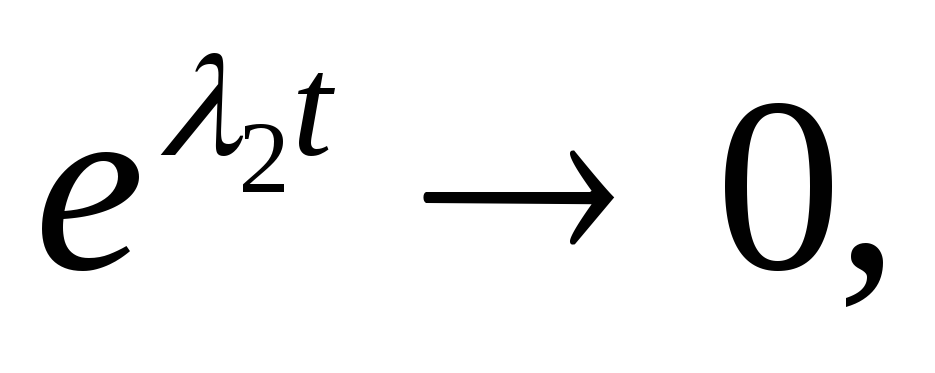=>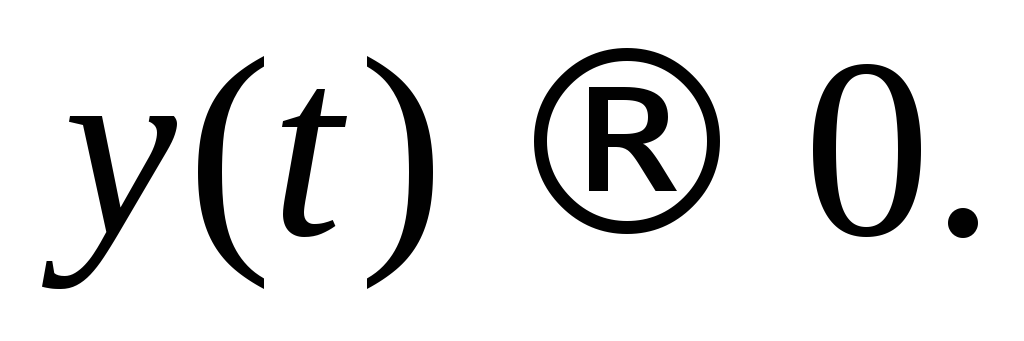Точка покоя называетсяустойчивым узлом.

При с₂=0 из (4) имеем:

Значит, траекториями являются лучи, входящие в начало координат с коэффициентами: Если с₁=0, то получаются лучи, входящие в начало координат с коэффициентами:

Пусть с₁≠0 и с₂≠0, |λ₁| > |λ₂|.

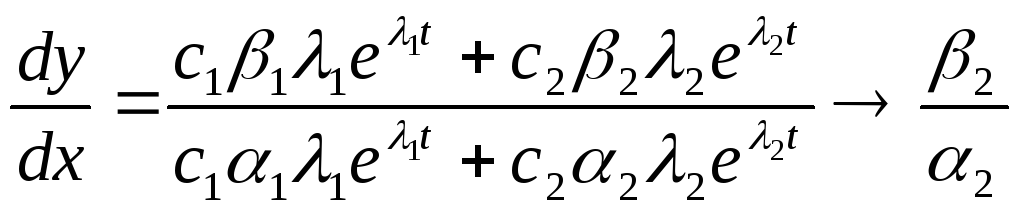
при Т.е. все траектории, исключая лучи в окрестности точки покоя (0;0) имеют направление луча:

2. Пусть λ₁>0, λ₂>0. Решение записано в виде (4). Если λ₁>0, λ₂>0, то расположение траектории такое же, как в предыдущем случае, но точки по траектории движутся в противоположном направлении. Точки такого рассматриваемого типа называютнеустойчивым узлом.

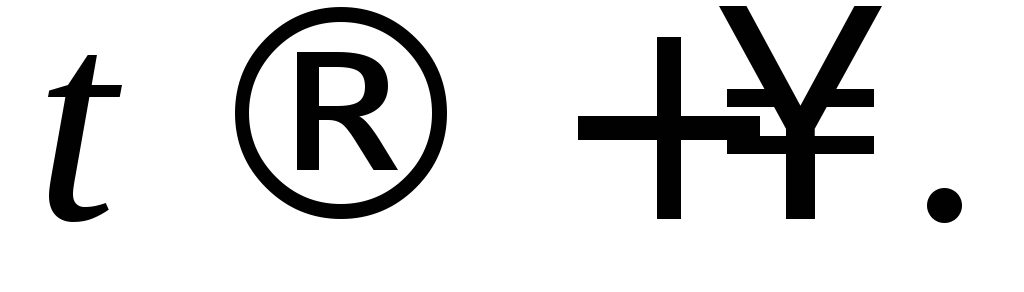3. Пусть λ₁>0, λ₂<0. В этом случае точка покоя неустойчива. Действительно, пусть в (4) с₂=0, тогда: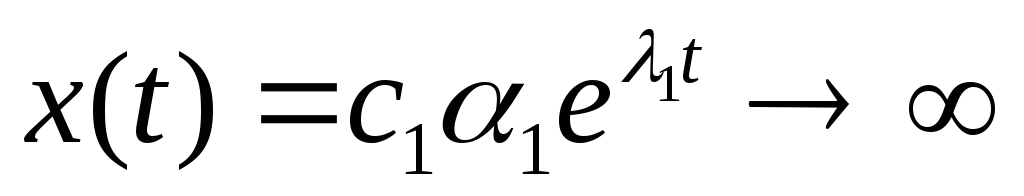

. => при движении по лучу точка уходит от точки покоя в -ть.

Пусть в (4) с₁=0, тогда:

=> при движении по лучу точка приближается к точке покоя.

П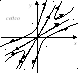усть Тогда можно убедиться, что при движении траектория покидает окрестность точки покоя. В этом случае, точка покоя называется седлом.

B) Корни λ₁, λ₂ характеристического уравнения (3) комплексные:

Общее решение системы (2) можно записать в виде:

где с₁, с₂ – постоянные коэффициенты;

c₁^*, с₂^* - некоторые линейные комбинации этих постоянных.

1)

То в (5)при а 2-е множители в (5) ограниченные периодические функции. В этом случае траекториями будут спирали, асимптотически приближающиеся к началу координат при Точка покоя x=0, y=0 асимптотически устойчива. Она называется устойчивым фокусом.

2)

Этот случай переходит в предыдущий, если рассматривать неа В этом случае траектории не отличаются от предыдущих траекторий, но при движение происходит в обратном направлении. Точка покоя неустойчива. Она называется неустойчивый фокус.

3)

Из (5) видно, что решением системы (2) будут периодические функции (т.к. в (5) 1-й множитель равен1,а функции периодические). Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемая в этом случае центром. Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, т.к.:

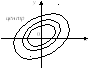
- этими кривыми являются логарифмические спирали, навивающиеся на начало координат, кот. достиг-ся в пределе при в зависимости от того, будет ли a<0 или a>0.

В этом случае точка покоя называется фокусом.

Если a=0, то ρ=с. Интегральными кривыми являются окружности с центром в начале координат. В этом случае точка покоя называется центром.

С) λ₁=λ₂ .

1) λ₁=λ₂ <0.

.

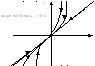
2) λ₁=λ₂ >0.

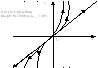неустойчивый вырожденный узел.