
- •51. Организация файловой системы fat
- •52. Организация файловой системы ext2
- •53. Язык регулярных выражений и его применение, шаблоны имен файлов
- •2)Символы – квантификаторы(повторители):
- •54. Пользовательский интерфейс ос
- •55. Язык сценариев ос
- •56. Процессы и механизмы многозадачности
- •57. Переменные величины в яп, их атрибуты, время жизни, область видимости
- •58. Типы данных в яп
- •59. Алгоритмы обработки массивов
- •60. Выражения и операции. Перегрузка операций.
- •61. Операторный базис языков программирования.
- •62. Функция как средство структурирования программы.
- •69. Механизмы создания и уничтожения объектов
- •70. Наследование в яп
- •Виртуальные функции
- •Синтаксис шаблона функции
- •Примеры определений шаблонов функций
- •Прототип шаблона функции
- •Использование шаблона функции
- •Специализация шаблонов функции
- •Шаблоны классов
- •Синтаксис шаблона класса
- •Пример определения шаблона класса
- •Использование шаблона класса
- •Векторы
- •Уравнение прямой
- •Общее уравнение прямой
- •Расстояние от точки до прямой
- •Углы между двумя прямыми, между прямой и плоскостью.
- •Общее уравнение плоскости
- •Уравнение плоскости
- •Уравнение поверхности:
- •35. Устойчивость решений дифференциальных уравнений
- •Простейшие типы точек покоя. Автономные динамические системы двух уравнений первого порядка. Типы особых точек на фазовой плоскости
- •39. Алгебра логики.
- •3. Основные законы логики.
- •5. Нормальные формы. Совершенные нормальные формы.
- •6. Арифметические операции в алгебре логики. Полином Жегалкина.
- •7. Полнота и замкнутость (примеры полных систем). Теорема Поста.
- •Вопрос 40 Графы и их свойства
- •41. Маршруты в графах и деревья.
- •42. Сети и алгоритмы на сетях.
- •43. Вероятность случайного события. Основные свойства вероятности.
- •44. Случайные величины и законы их распределения.
- •45. Числовые характеристики случайных величин.
- •46. Методы проверки статических гипотез.
- •47. Математические модели операций.
- •48. Матричные игры.
- •49.Линейное программирование. Симплекс-метод.
- •50. Выпуклое программирование.
- •2) Различные формы условий оптимальности.
- •74. Проектирование структуры реляционной базы данных. Метод er-диаграмм (сущность-связь).
- •75. Языки описания запросов. Язык sql.
- •Select [all | distinct] –команда выборки данных
Углы между двумя прямыми, между прямой и плоскостью.
Пусть
в пространстве даны две непараллельные
прямые
![]() и
и
![]() .
Возьмем произвол. точку А пространства
и проведем через нее прямые
.
Возьмем произвол. точку А пространства
и проведем через нее прямые
![]() и
и![]() соответственно параллельные прямым
соответственно параллельные прямым
![]() и
и
![]() .
Прямые
.
Прямые
![]() и
и![]() образуют
четыре угла с вершиной А. Каждый из этих
углов называется углом между прямыми
образуют
четыре угла с вершиной А. Каждый из этих
углов называется углом между прямыми![]() и
и
![]() .
Если
.
Если
![]() и
и
![]() -
направляющие векторы данных прямых
-
направляющие векторы данных прямых
![]() и
и
![]() ,
то угол
,
то угол
![]() между этими прямыми
вычисляется по формуле:
между этими прямыми
вычисляется по формуле:
![]() Условие
перпендикулярности двух прямых:
Условие
перпендикулярности двух прямых:
![]()
Прямая
d
параллельна плоскости
![]() тогда,
когда вектор
тогда,
когда вектор![]() параллелен плоскости
параллелен плоскости
![]() и
точка
и
точка
![]() не
лежит в этой плоскости :
не
лежит в этой плоскости :
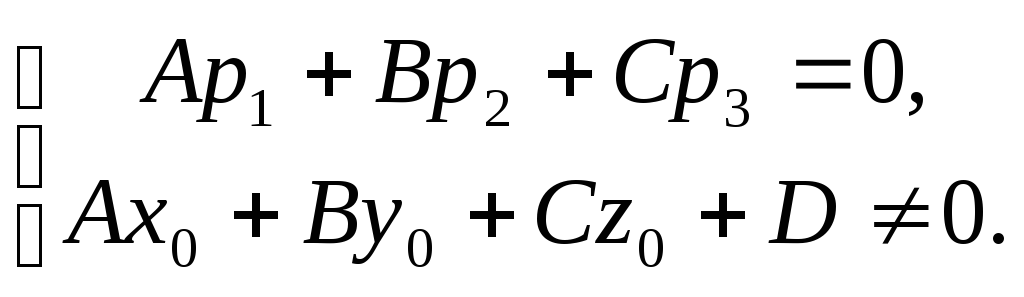
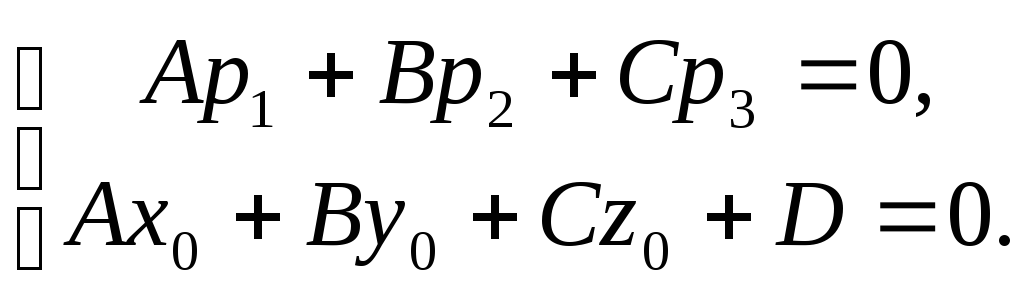 -
прямая лежит
в плоскости.
-
прямая лежит
в плоскости.
![]() - прямая
и плоскость пересекаются,
т.е. имеют одну общую точку.
- прямая
и плоскость пересекаются,
т.е. имеют одну общую точку.
Пусть
прямая d
имеет направляющий вектор![]() ,
а плоскость
,
а плоскость
![]() -
уравнение
-
уравнение
![]() Угол между
Угол между
![]() между
прямой d
и плоскостью
между
прямой d
и плоскостью
![]() :
:![]() или
или
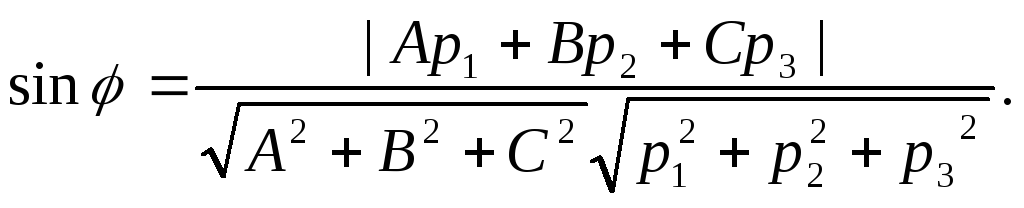
Общее уравнение плоскости
![]() ,
(1)
,
(1)
где
![]()
Любая плоскость есть поверхность первого порядка.
Расстояние
от точки
![]() до плоскости
до плоскости
![]() :
:
![]() .
.
![]() ,
,
![]() -
параллельные плоскости.
-
параллельные плоскости.
Две
пересекающиеся плоскости образуют
четыре двугранных угла, и любой из этих
углов называется углом
между данными плоскостями.
Т. к. векторы
![]() и
и
![]() перпендикулярны
данным плоскостям, то угол
перпендикулярны
данным плоскостям, то угол
![]() равен:
равен:
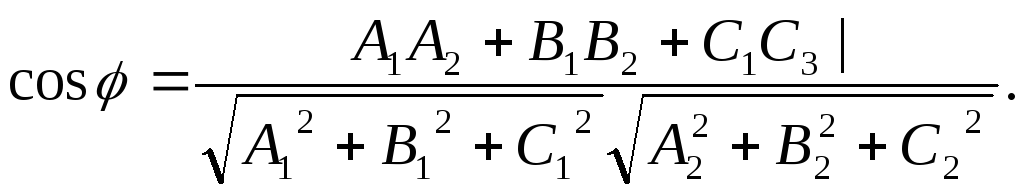
Плоскости
![]() -перпендикулярны
тогда, когда
-перпендикулярны
тогда, когда
![]() Т.е.,
когда
Т.е.,
когда
![]()
Уравнение плоскости
Рассмотрим
плоскость
![]() .
Множество L
всех векторов, параллельных плоскости
.
Множество L
всех векторов, параллельных плоскости
![]() ,
является двумерным векторным
подпространством трехмерного векторного
пространства V.
Подпространство L
назовем направляющим
подпространством
плоскости
,
является двумерным векторным
подпространством трехмерного векторного
пространства V.
Подпространство L
назовем направляющим
подпространством
плоскости
![]() .
.
Уравнение плоскости, заданной точкой и направляющим подпространством. Пусть в аффинной системе координат заданы своими координатами точка
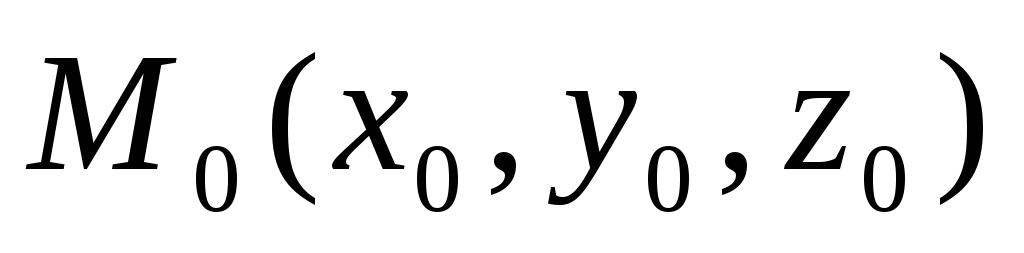 и
два неколлинеарных вектора:
и
два неколлинеарных вектора:
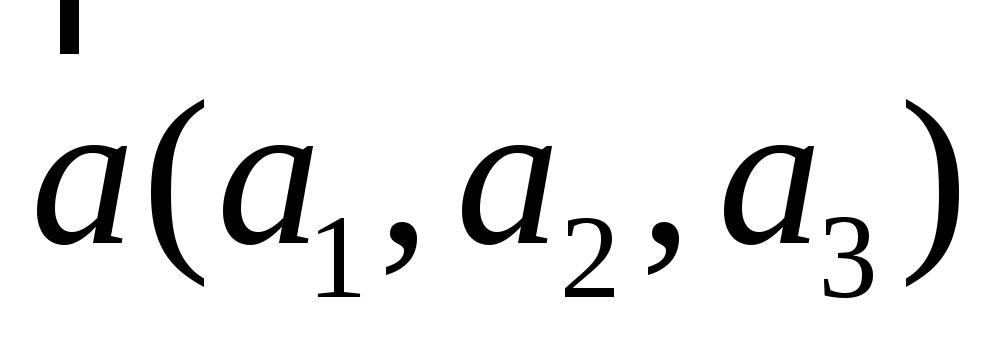 и
и
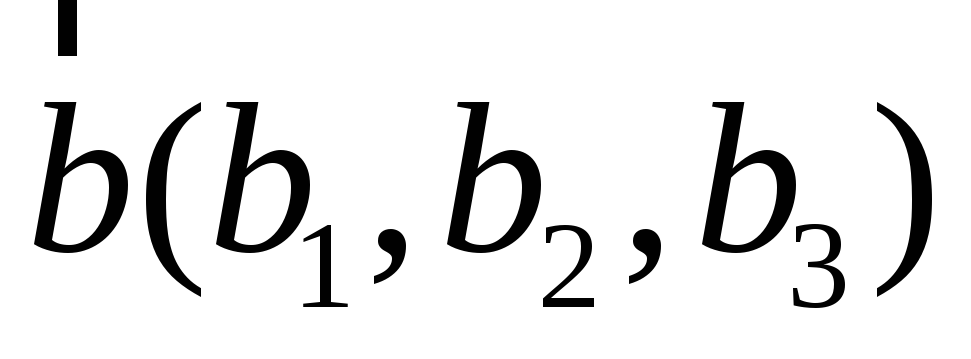 .
Уравнение
плоскости
.
Уравнение
плоскости
 ,
проходящей через точку
,
проходящей через точку и
имеющей направляющее подпространство
и
имеющей направляющее подпространство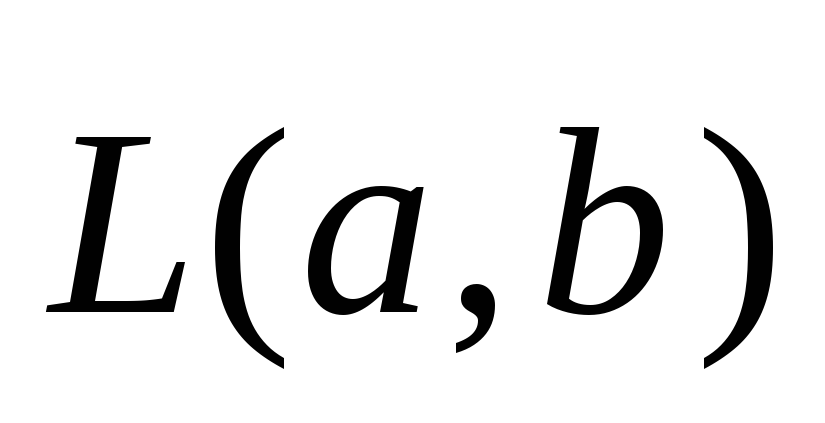 :
: (1)
(1)У
 равнение
плоскости, заданной тремя точками.
равнение
плоскости, заданной тремя точками.
Уравнение плоскости, заданной точкой и перпендикулярным вектором. Говорят, что вектор
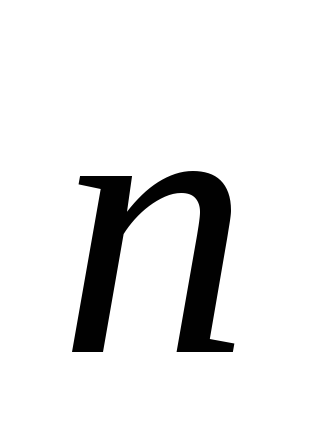 перпендикулярен
плоскости
перпендикулярен
плоскости
 ,
если вектор
,
если вектор
 перпендикулярен любому вектору из
направляющего подпространства плоскости
перпендикулярен любому вектору из
направляющего подпространства плоскости
 .
Точка
.
Точка
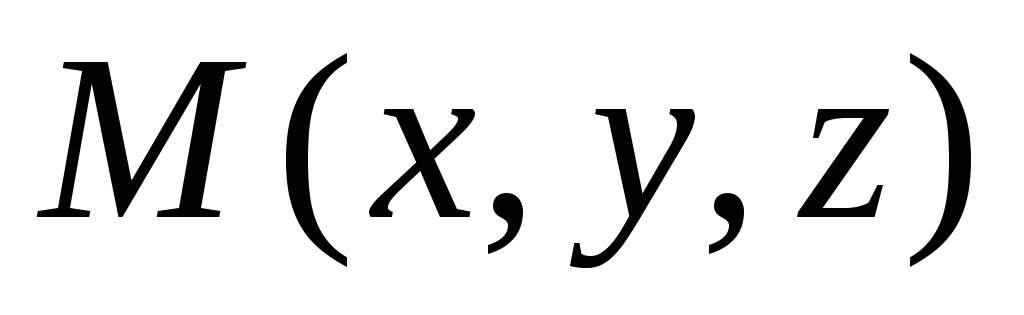 принадлежит
плоскости
принадлежит
плоскости тогда,
когда векторы
тогда,
когда векторы
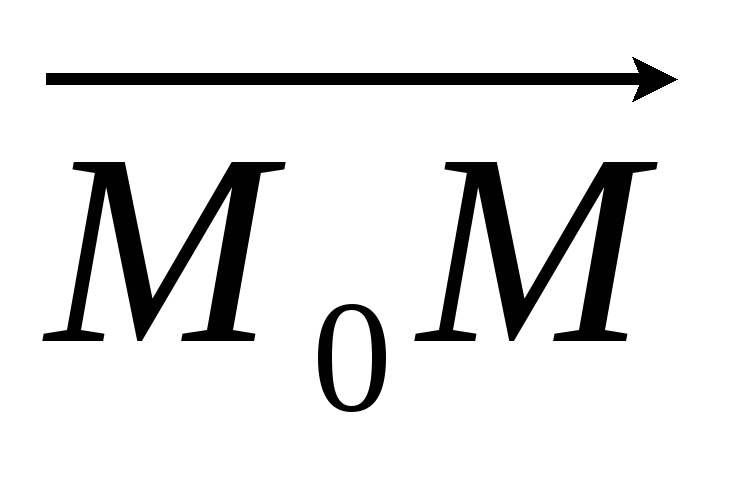 и
и
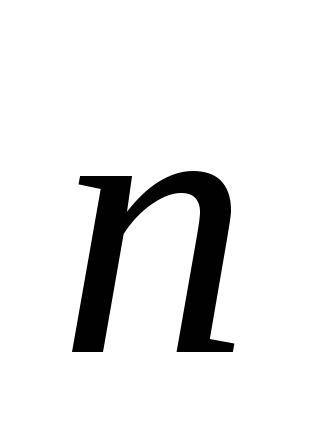 ортогональны,
т. е. их скалярное произведение =0:
ортогональны,
т. е. их скалярное произведение =0:
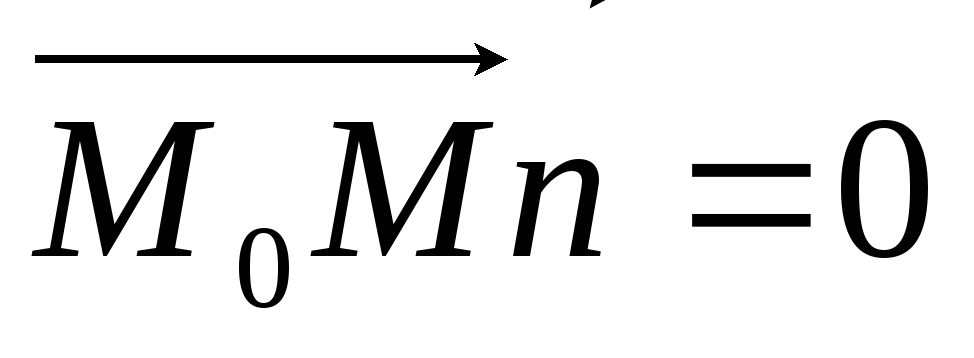 .Уравнение:
.Уравнение:
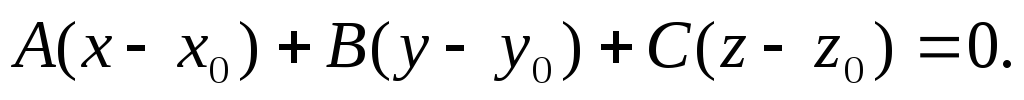 (3)
(3)П
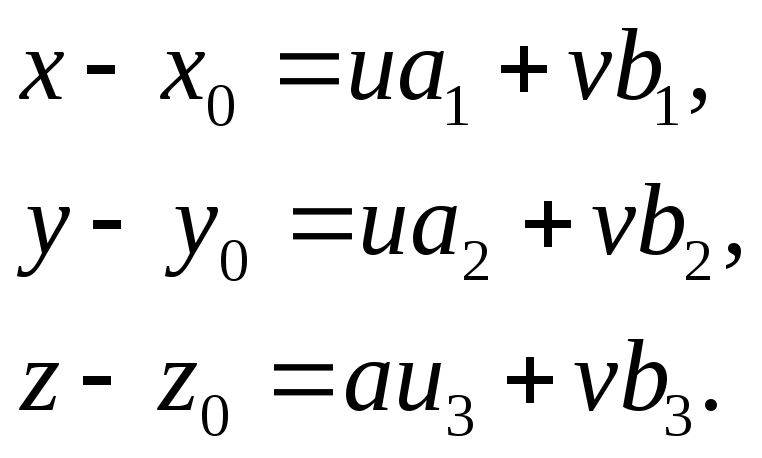 араметрическое
уравнение плоскости.Пусть
плоскость
араметрическое
уравнение плоскости.Пусть
плоскость
 проходит
через т.
проходит
через т.
 и
имеет направляющее подпространство
и
имеет направляющее подпространство
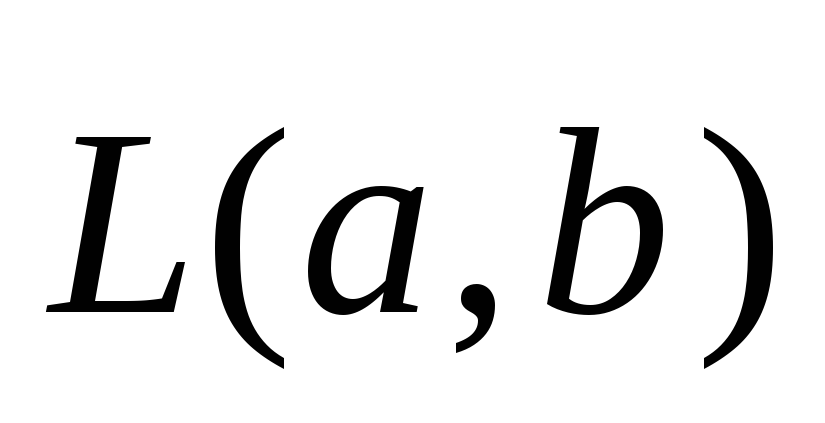 с
базисом
с
базисом
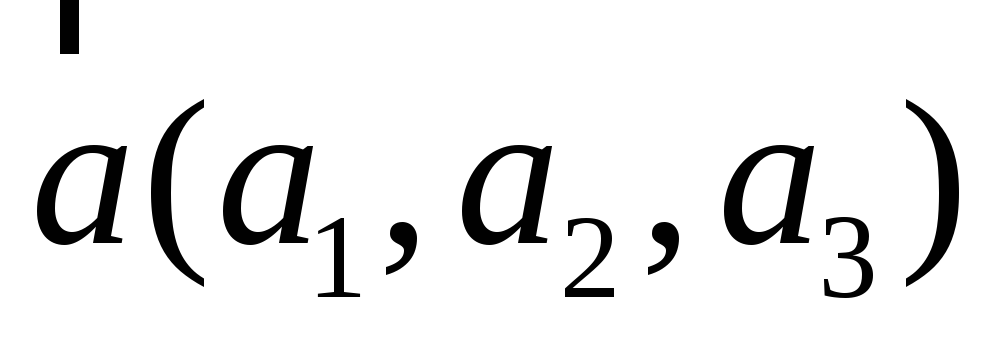 ,
,
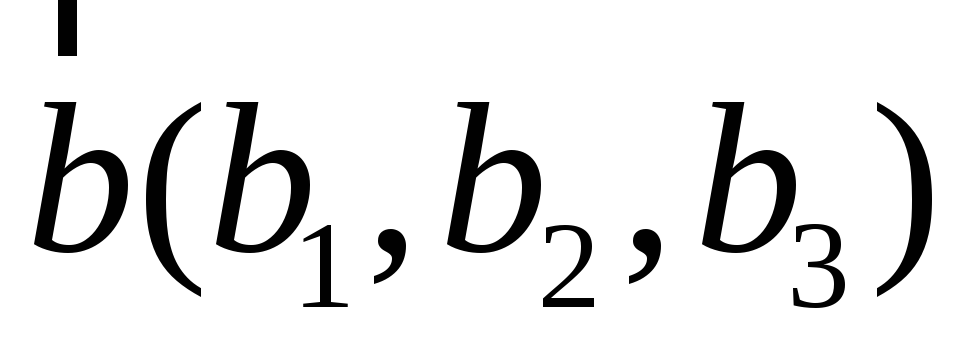 .
Точка
.
Точка
 принадлежит плоскости
принадлежит плоскости тогда,
когда:
тогда,
когда:
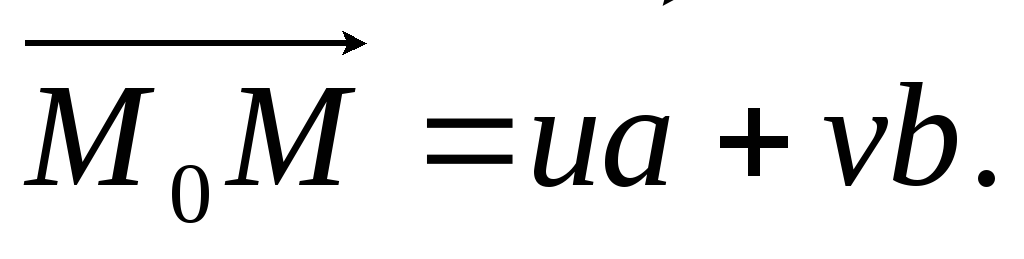 (4)
(4)
Равенства
(5) называются параметрическими
уравнениями
плоскости
![]() ,
а
,
а
![]() -
параметрами.
-
параметрами.
Уравнение поверхности:
35. Устойчивость решений дифференциальных уравнений
Устойчивость решений по Ляпунову
П![]()
![]() усть
дана система обыкновенных дифференциальных
уравнений (ОДУ):
усть
дана система обыкновенных дифференциальных
уравнений (ОДУ):
![]() (i = 1…n).
(i = 1…n).
![]() , где y
– вектор с координатами (y1,…,yn),
y = (y1,…,yn),
f = (f1,…,fn).
Норма:
, где y
– вектор с координатами (y1,…,yn),
y = (y1,…,yn),
f = (f1,…,fn).
Норма: ![]() Пусть начальные данные задаются при x
= x0.
Пусть начальные данные задаются при x
= x0.
Опр: решение
y = y0(x)
системы (1) называется устойчивым
по Ляпунову, при ![]() ,
если
,
если ![]() >
0
>
0 ![]() ,
x ≥ x0
для любого решения этой системы.
,
x ≥ x0
для любого решения этой системы.
|| y(x)
– y0(x)||
<![]() при
|| y(x0)–
y0(x0)|
<
при
|| y(x0)–
y0(x0)|
<![]() .
.
Если, кроме того, ![]() при достаточно малых || y(x)
– y0(x)||,
то решение
(2) называется асимптотически
устойчивым при
при достаточно малых || y(x)
– y0(x)||,
то решение
(2) называется асимптотически
устойчивым при ![]() .
При этом предполагается, что функция
y0(x)
определяется для всех x
≥ x0,
а система (1) определена в некоторой
окрестности y = y0(x),
вида: || y(x)
– y0(x)||
< M при x
≥ x0.
.
При этом предполагается, что функция
y0(x)
определяется для всех x
≥ x0,
а система (1) определена в некоторой
окрестности y = y0(x),
вида: || y(x)
– y0(x)||
< M при x
≥ x0.
Очевидно, всегда можно
рассматривать случай y0(x)![]() 0,
взяв вместо y(x)
новую неизвестную функцию y(x)
– y0(x).
Функции fi, yi
и х считаются действительными.
0,
взяв вместо y(x)
новую неизвестную функцию y(x)
– y0(x).
Функции fi, yi
и х считаются действительными.
Устойчивость означает, что
малые изменения начальных условий
приводят к малому отличию решений при
x ≥ x0,
а асимптотическая устойчивость означает,
что при малом отличии начальных данных,
решения неограниченно приближаются к
y0(x)
при ![]() .
.
![]()
Пример 1: (a = const, a ≠ 0). Начальное условие: y(x0) = y0.
Р ешение:
ешение:![]()
 y(x0)
= 0, y = 0.
y(x0)
= 0, y = 0.

 Решение
устойчиво асимптотически.
Решение
устойчиво асимптотически.
![]()
![]()

![]()

При исследовании устойчивости и асимптотической устойчивости важную роль играет теорема Ляпунова.
Теорема Ляпунова об устойчивости и асимптотической устойчивости:
Пусть для некоторого ![]() > 0 правая часть системы (1)определена
и непрерывна при
> 0 правая часть системы (1)определена
и непрерывна при ![]() и || y || <
и || y || < ![]() и f(x, 0)
и f(x, 0)![]() 0.
Пусть при тех же значениях y
существует непрерывно дифференцируемая
«функция Ляпунова»: V(y)
≥ 0 и равна нулю лишь в начале координат.
0.
Пусть при тех же значениях y
существует непрерывно дифференцируемая
«функция Ляпунова»: V(y)
≥ 0 и равна нулю лишь в начале координат.
а) Если ![]()
![]() то нулевое решение y(x)
то нулевое решение y(x)
![]() 0 системы (1) устойчиво.
0 системы (1) устойчиво.
б) Если ![]()
![]() где
где ![]() ≥
0 – некоторая непрерывная функция
(W(0)=0, W(y)≠0
при y≠0), равна нулю лишь
в начале координат, то нулевое решение
асимптотически устойчиво.
≥
0 – некоторая непрерывная функция
(W(0)=0, W(y)≠0
при y≠0), равна нулю лишь
в начале координат, то нулевое решение
асимптотически устойчиво.
Теорема имеет простой
геометрический смысл. Пусть n=2
и пусть линии V=c
(c=const)
замкнутые линии, содержащие начало
координат. Причем линия с меньшим
значением с лежит внутри линии с большим
значением с. Тогда (3) означает, что
интегральные линии, имеющие общую точку
с линией V=c,
не выходят из области, ограниченной
этой линией. Откуда и следует устойчивость
нулевых решений y1![]() 0, y2
0, y2![]() 0 (т.е. начало координат на плоскости
y1,
y2).
0 (т.е. начало координат на плоскости
y1,
y2).
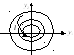 При
выполнении более сильного условия (4),
интегральные линии пересекают линию
V
При
выполнении более сильного условия (4),
интегральные линии пересекают линию
V![]() c
снаружи внутрь (см. рис.), т.к.
c
снаружи внутрь (см. рис.), т.к.
![]()
![]() (
(![]() > 0).
> 0).
![]() ,
следовательно, все интегральные линии,
при
,
следовательно, все интегральные линии,
при ![]() ,
→ к началу координат, что означает
асимптотическую устойчивость нулевого
решения.
,
→ к началу координат, что означает
асимптотическую устойчивость нулевого
решения.
Теорема Четаева о неустойчивости:
Если существует дифференцируемая функция V(y), удовлетворяющая в некотором замкнутом шаре Tr условиям:
в сколь угодно малой окрестности U начала координат
 область U0,
в которой V>0, причем
V=0 на лежащей в U
части границы U0;
область U0,
в которой V>0, причем
V=0 на лежащей в U
части границы U0;в области U0 производная
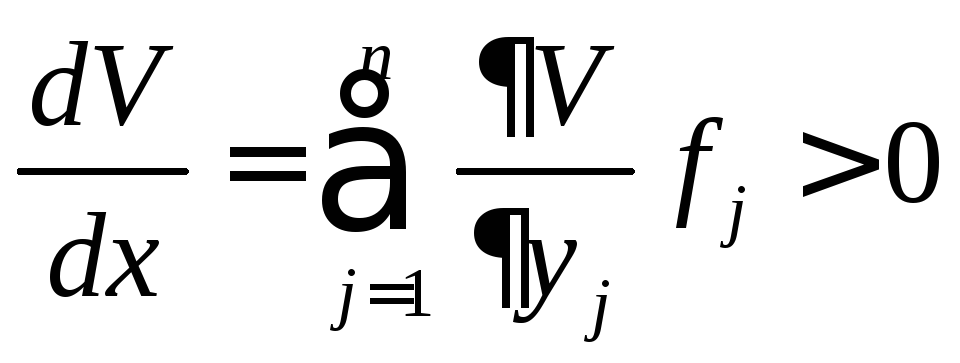 ,
причем в области, где
,
причем в области, где 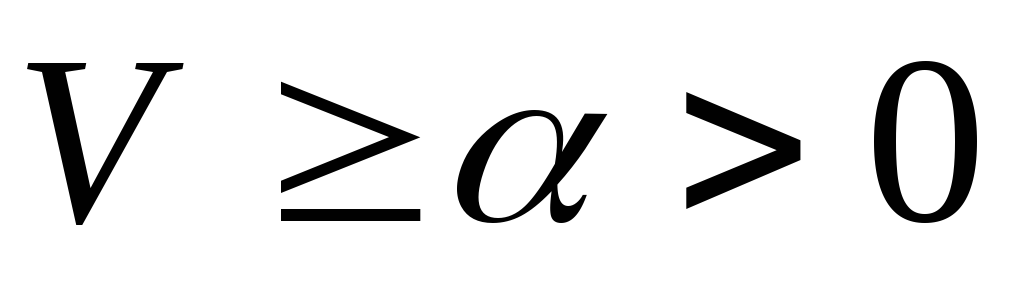 ,
производная
,
производная 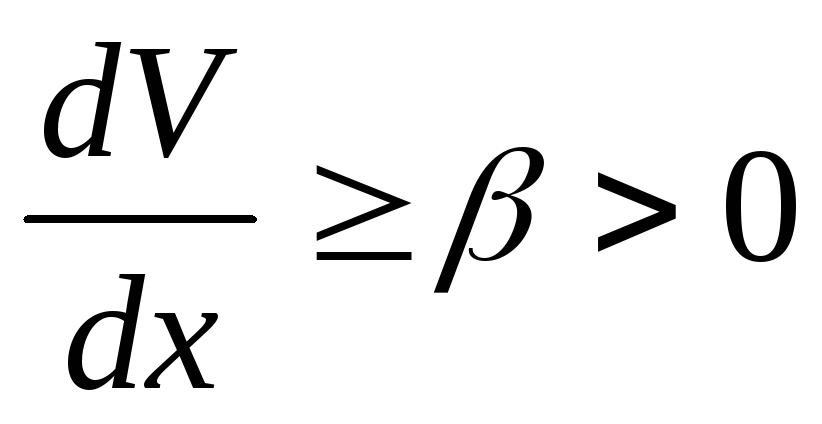 ,
,
то нулевое решение системы
(1) неустойчиво. y1![]() 0, y1
0, y1![]() 0,…,yn
0,…,yn![]() 0.
0.
Зад.Исследовать на устойчивость нулевое решение системы:
Пример 1: ![]()
![]() (
(![]() –
эта пара функций образует нулевое
решение системы)
–
эта пара функций образует нулевое
решение системы)
![]() (функция V-неотрицательная,
имеет непрерывные частные производные,
обращается в 0 в единственной точке)
(функция V-неотрицательная,
имеет непрерывные частные производные,
обращается в 0 в единственной точке)
![]()
Условие (3) выполнено, ![]() нулевое решение устойчиво. Асимптотической
устойчивости нет. Интегральными линиями
будут окрестности, которые при
нулевое решение устойчиво. Асимптотической
устойчивости нет. Интегральными линиями
будут окрестности, которые при ![]() не → к нулю.
не → к нулю.
Метод функций Ляпунова оказывается универсальным и эффективным методом для широкого круга задач теории устойчивости. Недостаток метода в том, что не существует достаточно общего конструктивного способа для нахождения функций Ляпунова.
В простейших случаях функции Ляпунова следует искать в виде:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пусть функции (1) fi имеют вид:
![]()
![]() где
где 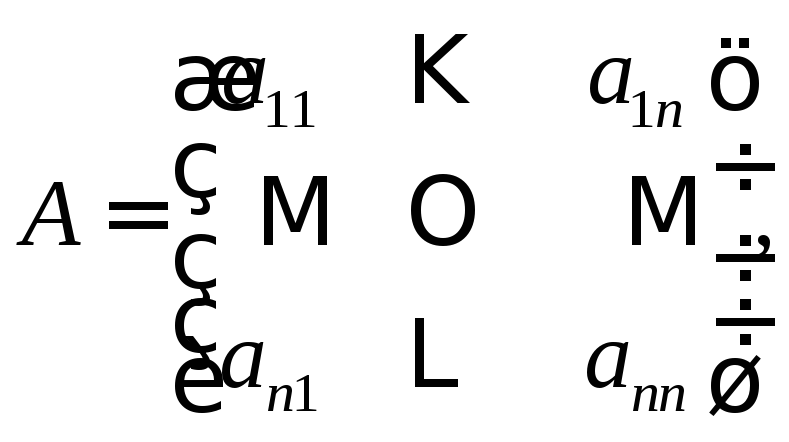
![]()
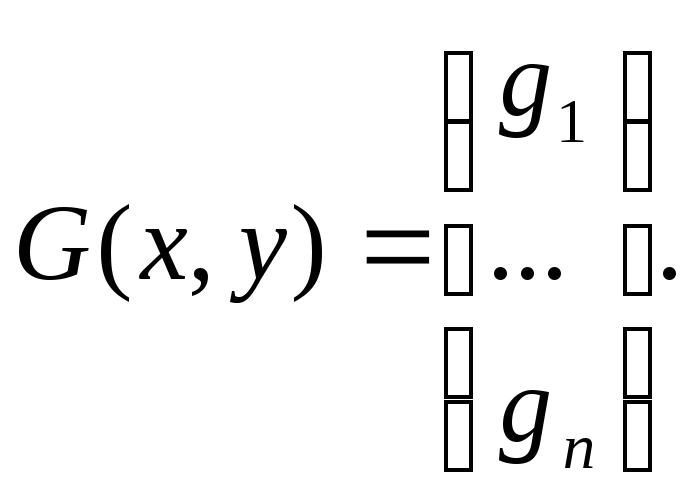
Теорема Ляпунова об устойчивости по первому приближению:
Пусть ![]()
При всех x ≥
x0 и
при всех y, с достаточно
малой нормой ||y||, норма
![]() (α, М - const),
и функции gi непрерывны
по совокупности переменных. Тогда, если
действительные части всех корней
уравнения | λE – A
| = 0 отрицательны, то нулевое решение
системы (1) асимптотически устойчиво.
Если хотя бы один из корней имеет
положительную действительную часть,
то нулевое решение не устойчиво. Без
док-ва.
(α, М - const),
и функции gi непрерывны
по совокупности переменных. Тогда, если
действительные части всех корней
уравнения | λE – A
| = 0 отрицательны, то нулевое решение
системы (1) асимптотически устойчиво.
Если хотя бы один из корней имеет
положительную действительную часть,
то нулевое решение не устойчиво. Без
док-ва.
Д![]() ля
определения знака действительной части
корня уравнения | λE – A
| = 0 нет необходимости решать это
уравнение. Определитель нужно раскрыть
и записать его в виде многочлена
относительно λ:
ля
определения знака действительной части
корня уравнения | λE – A
| = 0 нет необходимости решать это
уравнение. Определитель нужно раскрыть
и записать его в виде многочлена
относительно λ: ![]()
![]() Для того, чтобы действительные
части всех корней уравнения (5) были
положительными, н. и д. выполнение одного
из условий:
Для того, чтобы действительные
части всех корней уравнения (5) были
положительными, н. и д. выполнение одного
из условий:
а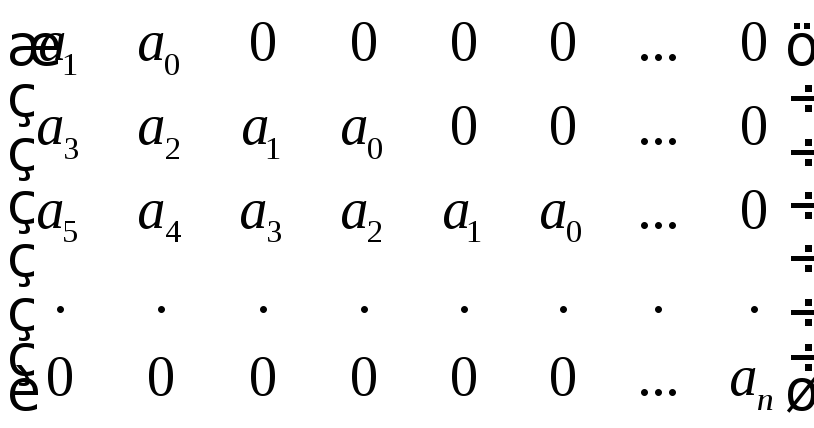 )
условие Гаусса – Гурвица: положительны
все главные миноры матрицы Гурвица:
)
условие Гаусса – Гурвица: положительны
все главные миноры матрицы Гурвица:






б) условие Льенара – Шипора: ai > 0 (i=1…n), миноры ∆n-1 > 0, ∆n-3 >0, ∆n-5 >0,… .
∆1
= ![]() ,
∆2
=
,
∆2
= ![]() ∆3
=
∆3
= 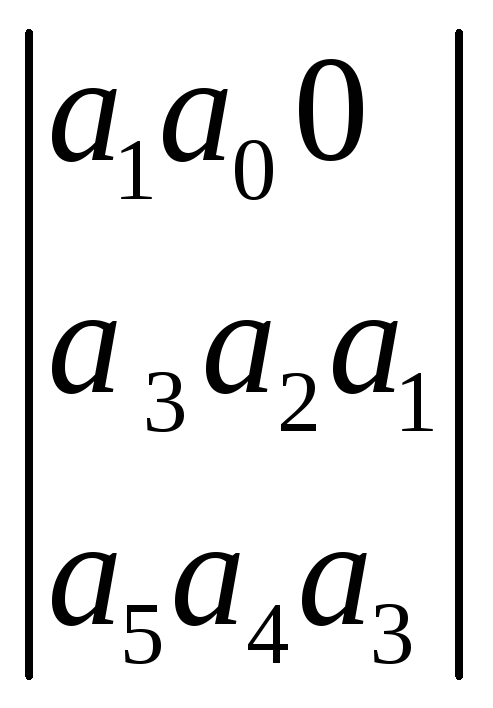 ,…
.
,…
.
