6. Арифметические операции в алгебре логики. Полином Жегалкина.

, где - арифметические операции сложение и умножение по модулю 2.

Полиномом Жегалкинаназывается полином вида

, где

Суммирование ведётся по всем несовпадающим наборам .

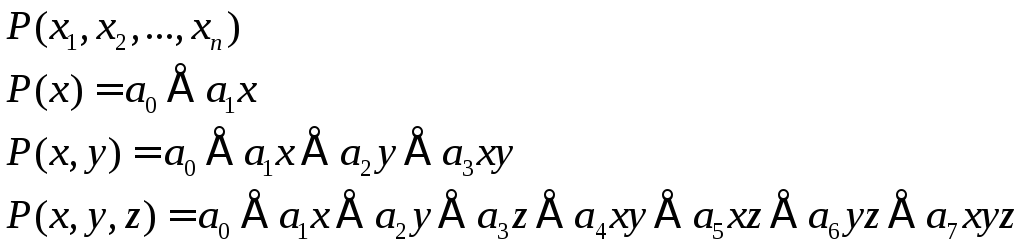
Теорема. Для любой булевой функции существует единственный полином Жегалкина.

Булева функция от переменных называется линейной, если её полином Жегалкина имеет вид: .

7. Полнота и замкнутость (примеры полных систем). Теорема Поста.

(1) – система булевых функций.

Система (1) называется полной, если любую булеву функцию можно реализовать формулой в этой системе.

Примером полной системы является сам класс булевой функции.

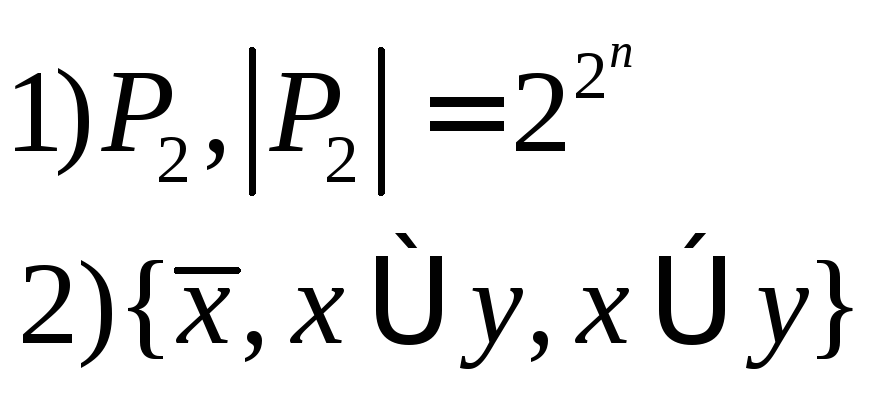
Пусть даны две системы булевых функций (1) (2) относительно которых известно, что (1) – полная система и каждая функция первой системы представляется в виде суперпозиции функций (2) системы, тогда (2) – полная система. Система (1) называется функционально замкнутым классом, если любая суперпозиция функций этой системы принадлежит ей же. Функционально замкнутые классы отличные от пустого класса и от класса называются собственными функционально замкнутыми классами. Рассмотрим важнейшие функционально замкнутые классы.1. - это класс функций, сохраняющий ноль, т. е. функций для которых Пример. .2. - это класс функций, сохраняющий единицу, т. е. функций для которых Пример. .3. - это класс линейных функций, т. е. функции, для которых полином Жегалкина является линейным относительно каждой переменной. . 4. - это класс монотонных функций. Пусть

, где - двоичные векторы, являющиеся наборами значений переменных ; Вектор предшествует или младше вектора , если , такие наборы называются сравнимыми. Свойства отношений. 1) - рефлексивность 2) и - симметричность 3) и - транзитивность.

Булева функция называется монотонной, если для каждой пары сравнимых наборов. Пример монотонных функций.1) 2)

5. - это класс самодвойственных функций, для которых Теорема Поста. Для того чтобы система булевых функций (1) была полной необходимо и достаточно, чтобы она целиком не содержалась ни в одном из пяти функционально замкнутых классов. Для проверки полноты системы функцийсоставляется специальная критериальная таблица:

	+	-	-	+	-
	+	-	+	-	-
	-	+	+	+	-

По теореме Поста система является полной, если каждый столбец таблицы содержит хотя бы один « - ».

Вопрос 40 Графы и их свойства

Графические представления - удобный способ иллюстрации содержания различных понятий, относящихся к другим способам формализованных представлений. Мощным и наиболее исследованным классом объектов, относящихся к графическим представлениям, являются так называемые графы, изучаемые в теории графов.

Графическое представление в узком смысле – это описание исследуемой системы, процесса, явления средствами теории графов в виде совокупности двух классов объектов: вершин и соединяющих их линий – ребер или дуг. Графы и их составляющие характеризуются определенными свойствами и набором допустимых преобразований (операций) над ними.

Графом G называется совокупность двух множеств: вершин V и ребер E, между элементами которых определено отношение инцидентности – каждое ребро eE инцидентно ровно двум вершинам v, v , которые оно соединяет. При этом вершина v (v) и ребро e называются инцидентными друг другу, а вершины v и v, являющиеся для ребра e концевыми точками, называются смежными. Часто вместо v и eE пишут соответственно

Ребро, соединяющее две вершины, может иметь направление от одной вершины к другой; в этом случае оно называется направленным, или ориентированным, или дугой и изображается стрелкой, направленной от вершины, называемой началом, к вершине, именуемой концом.

Граф, содержащий направленные ребра (дуги) с началом v и концом v, называется ориентированным (орграфом), а ненаправленные – неориентированным (назовем н - графом).

Ребра, инцидентные одной и той же паре вершин, называются параллельными, или кратными. Граф, содержащий кратные ребра, именуется мультиграфом. Ребро, концевые вершины которого совпадают, называется петлей.

Граф называется конечным, если множество его элементов (вершин и ребер) конечно, и пустым, если его множество вершин V (а значит и ребер E) пусто. Граф без петель и кратных ребер именуется полным, если каждая пара вершин соединена ребром. Простой граф – граф, не имеющий петель или кратных ребер

Дополнением графа G называется граф , имеющий те же вершины, что и граф G, и содержащий только те ребра, которые нужно добавить к графу G, чтобы получить полный граф.

Каждому неориентированному графу канонически соответствует ориентированный граф с тем же множеством вершин, в котором каждое ребро заменено двумя ориентированными ребрами, инцидентными тем же вершинам и имеющими противоположные направления.

Локальной степенью (или просто степенью) вершины v н-графа G называется количество ребер (v), инцидентных вершине v. В н – графе сумма степеней всех вершин равна удвоенному числу ребер m графа, т.е. четна (предполагается, что в графе с петлями петля дает вклад 2 в степень вершины):

= 2m,

Отсюда следует, что в н – графе число вершин нечетной степени четно. Граф, у которого вершины имеют одну и ту же валентность r называют правильным или r-валентным. Вершина изолирована, если её валентность (степень)=0.

Теорема. Во всяком графе с n вершинами всегда сущ-ет по меньшей мере 2 с одинаковыми степенями.

Для вершин орграфа определяются две локальные степени:

• (v) – число ребер с началом в вершине v, или количество выходящих из v ребер;

• (v) – количество входящих в v ребер, для которых эта вершина является концом.

В орграфе суммы степеней всех вершин (v) и (v) равны количеству ребер m этого графа, а значит и равны между собой:

Графы и равны, т.е. = , если их множества вершин и ребер (выраженных через пары инцидентных им вершин) совпадают: . Граф G считается полностью заданным в строгом смысле, если нумерация его вершин и ребер зафиксирована. Графы, отличающиеся только нумерацией вершин и ребер, называются изоморфными.

Типы и способы задания.

Задать граф – значит описать множества его вершин и ребер, а также отношение инцидентности. Для описания вершин и ребер достаточно их занумеровать. Пусть вершины графа G; ребра. Отношение инцидентности задается:

1. по определению (V,E, отношение инцидентности)

2. графически

3. Матричный способ (матрицей инцидентности)

Матрицей инцидентности размера : по вертикали и горизонтали указываются вершины и ребра соответственно, а на пересечение i – й вершины и j –го ребра в случае неориентированного графа проставляется 1, если они инцидентны, и 0 – в противном случае, т.е.

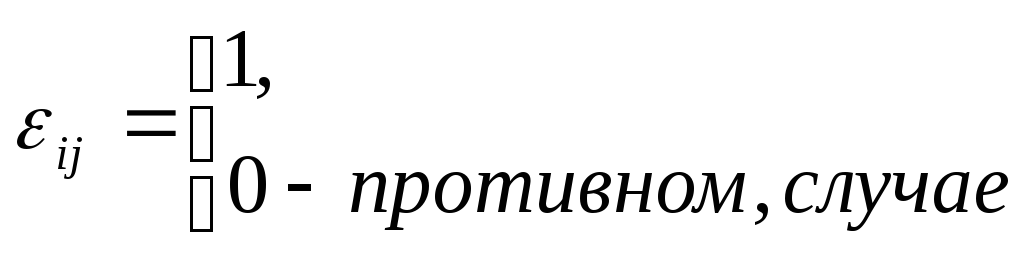если ребро инцидентно вершине ,а в случае орграфа: -1, если вершина является началом ребра, 1- если вершина является концом ребра, и 0 – если вершина и ребро не инцидентны; если некоторая вершина является для ребра и началом, и концом (т.е. ребро - петля), проставляется любое другое число, например 2.

4. Списком ребер графа, представленным двумя столбцами: в левом перечисляются все ребра 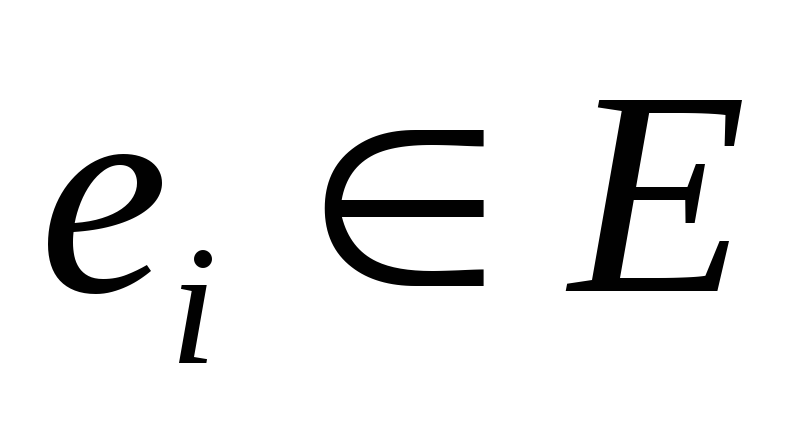, а в правом – инцидентные ему вершины ; для н – графа порядок вершин в строке произволен, для орграфа первым стоит номер начала ребра;

5. Матрицей смежности - квадратной матрицей размера : по вертикали и горизонтали перечисляются все вершины 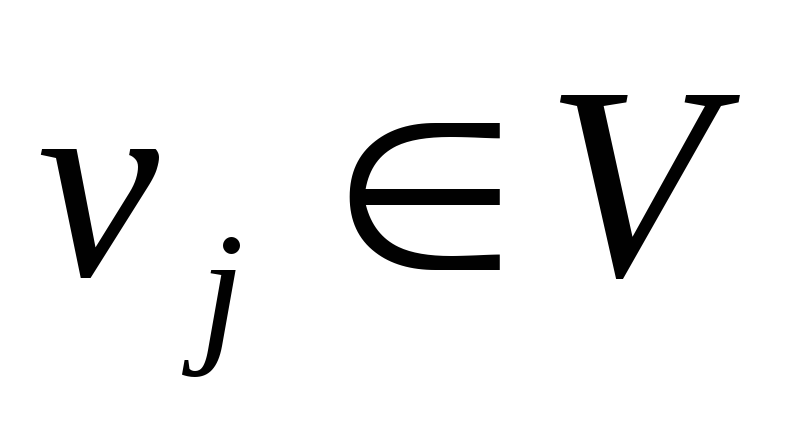, а на пересечении k –й и l –й вершин в случае н – графа проставляется число, равное числу ребер с началом в k – й вершине и концом в l –й.

Если два графа равны, то их матрицы совпадают. Если в графе поменять нумерацию вершин, матрицы (и список ребер) в общем случае изменяются, т.е. вид матриц и списка ребер зависит от нумерации вершин и ребер графа. Строго говоря, граф считается полностью заданным, если нумерация его вершин зафиксирована.

Операции над частями графа.

Граф Н называется частью графа G, , если множество его вершин V(G) и ребер E(H) содержатся в множествах вершин V(G) и ребер E(H) соответственно, т.е. V(H)V(G) и .

Если V(H)=V(G), часть Н графа П называется суграфом. Суграф н является покрывающим для н – графа G, если любая вершина графа G инцидентна хотя бы одному ребру из Н.

Подграфом графа G(V) с множеством вершин называется часть, которой принадлежат все ребра с обоими концами из .

Над частями графа G могут производиться следующие операции:

• Дополнение к части Н – определяется множеством всех ребер графа G, не принадлежащих Н: E(H), ;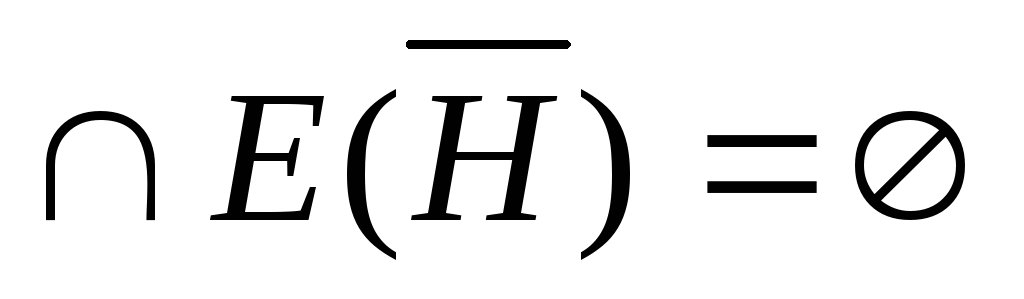

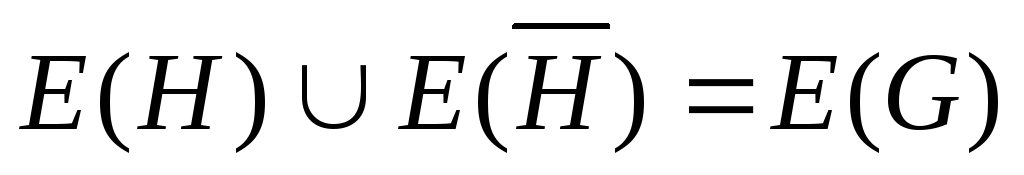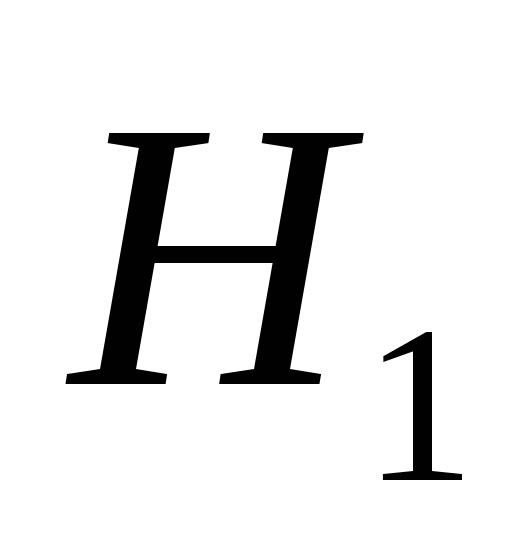• Сумма частей и графа G.

и;

• Произведение:

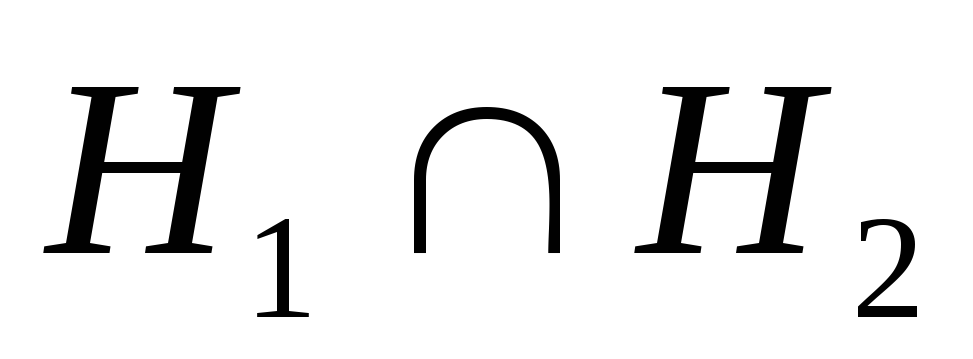и.

Две части и не пересекаются по вершинам, если они не имеют общих вершин , а значит , и общих ребер . Части и не пересекаются по ребрам, если . Если , то сумма называется прямой.

Графы и бинарные отношения: отношению R, заданному на множестве V, взаимно однозначно соответствует ориентированный граф G(R) без кратных ребер с множеством вершин V, в котором ребро существует, только если выполнено R .

Изображение графа, в котором никакие 2 ребра не имеют общих точек, кроме их общей вершины, наз. плоским представлением графа. Граф, имеющий плоское представление, наз. плоским. Граф, изоморфный плоскому графу, наз. планарным. Н – часть графа G, если соответствующее множество вершин является подмножеством множества вершин G, и множество ребер тоже.

.

Последовательность ребер, в которой каждая пара соседних имеет общую вершину, наз. маршрутом.

Путем из вершины в наз. такой соединяющий маршрут, в котором каждое ребро не встречается более одного раза.

Две вершины в графа G наз. связными, если в графе существует соединяющий их путь.

Граф G наз. связным, если для каждой пары различных вершин существует соединяющий их путь. Граф G наз. несвязным, если существует хотя бы одна пара вершин явл. несвязной.

Теорема Понтрягина – Куратовского: Граф является плоским т. и т.т., когда он не имеет подграфом граф типа1 или граф типа 2(др. словами: для того, чтобы граф был плоским необходимо и достаточно, чтобы он не содержал внутри себя никакого графа, которого можно было сжать до 5- и 6 – угольного графа).

Деревом называется всякий связный граф, не имеющий циклов.

Существует граф G связный с множеством вершин v деревом покрытия графа G или покрывающим деревом называется подграф с тем же множеством вершин, которое является деревом.

Теорема Эйлера: для любого плоского графа без перегородок справедливо соотношение

v– e + f = 2, v-множество вершин

е-множество ребер

f-множество граней

Доказательство:(проведем метод математической индукции по числу граней).

пусть f=1, следовательно, G – дерево v-(v-1)+1=2, т.е. 2=2

f=2 v-v+2=2, т.е. 2=2р

предположим, что формула справедлива для графа с f гранями. Докажем, что граней f+1. Цикл, ограничивающий эту грань, содержит r ребер, тогда вершин добавляем (r-1)

(Выделением покрывающего дерева)

Будем удалять ребра в плоском графе до тех пор, пока не получим суграфа, являющийся покрывающим деревом. Каждое удаление ребра уменьшает количество граней и ребер на 1, а соотношение v-e+f остается неизменным, следовательно, эта величина будет одинаковой как у исходного графа, так и у его покрывающего дерева, а для дерева v– e + f = 2. ч.т.д.