
Аналитическая геометрия - В.М. Гордиенко / Lecture 1-9
.pdf
Лекция 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Площадь параллелограмма, построенного на паре векторов |
|
||||||||||||||||||||
a; b 2 V |
dim V 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
a; b = |
a |
j j |
b |
j |
sin ' . |
|
|
|
|
|
|
|
|
|
|||||||
S |
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Т.к., |
ha; bi = jaj jbj cos ' , |
|
|
|
|
|
|
|
|||||||||||||
то |
sin ' = p1 cos2 ' = |
|
|
|
|
|
|
|
|
||||||||||||
= s1 |
ha; bi2 |
|
= |
h |
a; a |
b; bi ha; bi2 |
|
|
|||||||||||||
a |
2 |
j |
b |
|
2 |
|
|
i ha |
j j |
b |
j |
|
. |
|
|
||||||
|
j |
j |
|
|
|
j |
|
p |
|
|
|
j |
|
|
|
|
|
||||
Поэтому, S a; b = pha; ai hb; bi ha; bi2 . |
|
|
|||||||||||||||||||
Таким образом, |
|
|
|
|
S a; b |
= sdet |
|
a; a |
a; b |
|
|
||||||||||
|
|
|
|
ha; bi |
hb; bi . |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
i |
h |
i |
|
|
Аналитическая геометрия (1-ый сем.) |
|
|
|
Лекция 9 |
|
|
|
|
29 октября 2011 г. |
1 / 35 |
|||||||||||

Векторное произведение
V евклидовое , ориентированное , dim V = 3 , a; b 2 V.
Определение
Векторным произведением неколлинеарных векторов a и b
называется вектор c |
такой, что: |
c ? a ; c ? b |
т.е., hc; ai = hc; bi = 0 , |
векторы a; b; c |
образуют базис ориентированный |
положительно , |
|
 jcj = S a; b = jaj jbj sin ' . Если a и b коллинеарны, то c = 0 .
jcj = S a; b = jaj jbj sin ' . Если a и b коллинеарны, то c = 0 .
Обозначение: c = a b = a b = a; b .
Первое свойство определяет ось вектора c , второе направление на оси,
третье длину вектора c.
Аналитическая геометрия (1-ый сем.) |
Лекция 9 |
29 октября 2011 г. |
2 / 35 |
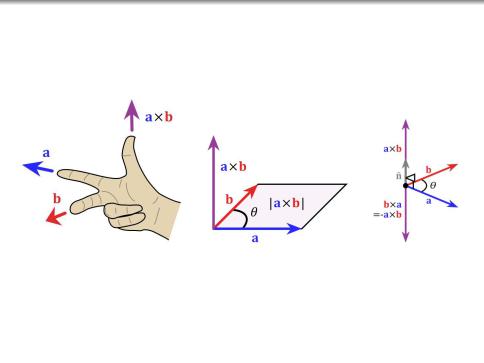
Часто в качестве положительной ориентации выбирается правая
Аналитическая геометрия (1-ый сем.) |
Лекция 9 |
29 октября 2011 г. |
3 / 35 |

Свойства векторного произведения
1) ka b = k a b = a kb
2) |
b a = a b |
3) |
a b = 0 () a; b линейно коллинеарны |
|
(в частности, 8a 2 V выполняется a a = 0 ) |
Пусть векторы i; j; k 2 V образуют ортонормированный положительно ориентированный базис, тогда
4) i j = k ; |
j k = i ; |
k i = j ; |
j i = k ; |
k j = i ; |
i k = j ; |
i i = 0 ; |
j j = 0 ; |
k k = 0 : |
5) a1 + a2 b = a1 b + a2 b ,
|
|
будет позже. |
a b1 + b2 |
= a b1 + a b2 |
Аналитическая геометрия (1-ый сем.) |
Лекция 9 |
29 октября 2011 г. |
4 / 35 |

Определение
Смешанным произведением векторов a; b; c
в трёхмерном евклидовом ориентированном пространстве называется число (a; b; c) = h[a b]; ci.
Теорема
Пусть векторы a; b; c некомпланарны и V объём параллелепипеда, натянутого на приведённые к общему началу векторы a; b; c . Тогда
( V если a; b; c положительно ориентированы
(a; b; c) =
V если a; b; c отрицательно ориентированы .
Если векторы a; b; c компланарны, то (a; b; c) = 0 .
c |
b |
a |
|
b |
|
a |
c |
Аналитическая геометрия (1-ый сем.) |
Лекция 9 |
29 октября 2011 г. |
5 / 35 |
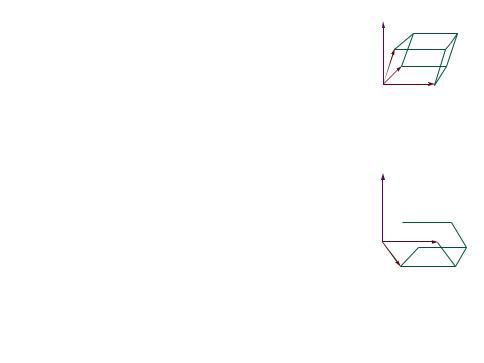
J Пусть векторы a; b; c некомпланарны. Обозначим d = a b .
(a; b; c) = hd; ci = jdj jcj cos dc = jdj , где = jcj cos dc
ясно что, j j высота параллелепипеда,
и, значит, j(a; b; c)j = V объём параллелепипеда.
d=a b
b
c
b
a
Покажем что, знак (a; b; c) совпадает с ориентацией векторов a; b; c.
Пусть c = a + b + d , тогда hd; ci = jdj2,
|
|
2 |
0 |
|
3 |
|
|
|
1 |
|
5 |
= [ a b d ] C, |
|
|
|
0 |
1 |
|
||
[ a b c ] = [ a b d ] 40 0 |
|
|||||
|
hd; ci |
(a; b; c) |
|
|||
det C = = |
|
= |
|
|
, |
|
jdj2 |
jdj2 |
|
||||
векторы a; b; d ориентированы положительно (по определению векторного произведения).
Значит, векторы a; b; c ориентированы положительно
() (a; b; c) > 0 .
d=a b
b
b  a
a
c
()

Пусть векторы |
a; b; c компланарны, |
|
покажем что, |
(a; b; c) = 0 . |
|
Имеем a + b + c = 0 , |
|
|
если 6= 0 , |
то |
|
(a; b; c) = hd; ci = hd; ai hd; bi = 0 ; |
||
если = 0 , |
то векторы a; b коллинеарны, |
|
значит, d = a b = 0 , |
I |
|
и снова (a; b; c) = hd; ci = 0 . |
||
Следствие |
|
|
Векторы a; b; c компланарны () |
(a; b; c) = 0 . |
|
Аналитическая геометрия (1-ый сем.) |
Лекция 9 |
29 октября 2011 г. |
7 / 35 |

Следствие
(a; b; c) = (b; c; a) = (c; a; b) =
= (b; a; c) = (a; c; b) = (c; b; a).
JДостаточно заметить, что тройки векторов
fa; b; cg; fb; c; ag; fc; a; bg
имеют одинаковую ориентацию, противоположную ориентации троек векторов fb; a; cg; fa; c; bg; fc; b; ag . I
Следствие
(a; b; c) = h[a b]; ci = ha; [b c]i.
Аналитическая геометрия (1-ый сем.) |
Лекция 9 |
29 октября 2011 г. |
8 / 35 |

Следствие
Смешанное произведение (a; b; c) линейно по каждому аргументу.
JИз определения смешанного произведения
(a; b; c) = h[a b]; ci и свойств скалярного произведения сразу вытекает линейность по третьему аргументу:
(a; b; k1c1 + k2c2) = k1(a; b; c1) + k2(a; b; c2) .
Т.к. (a; b; c) = (b; c; a) = (c; a; b) , то имеет место линейность по первому и второму аргументам
(k1a1 + k2a2; b; c) = k1(a; b; c) + k2(a; b; c) ,
(a; k1b1 + k2b2; c) = k1(a; b; c) + k2(a; b; c) . I
Аналитическая геометрия (1-ый сем.) |
Лекция 9 |
29 октября 2011 г. |
9 / 35 |
Докажем свойство 5) векторного произведения.
5) a1 + a2 b = a1 b + a2 b
JРассмотрим вектор d = a1 + a2 b a1 b a2 b . Имеем
hd; di = (a1 + a2; b; d) (a1; b; d) (a2; b; d) = 0 =)
=) d = 0 . I
Аналитическая геометрия (1-ый сем.) |
Лекция 9 |
29 октября 2011 г. |
10 / 35 |
