
Аналитическая геометрия - В.М. Гордиенко / Lecture 1-4
.pdf
Институт математики СО РАН им. С.Л. Соболева

Лекция 4
Аффинные пространства
Для аксиоматического определения аффинного пространства используем наглядные соображения о нашем трёхмерном пространстве.
Важные наблюдения:
A •
A
•
A •
A
•
a
B
•
B
•
• C
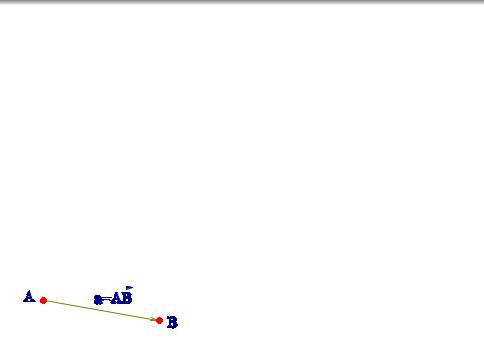
 имеются точки fAg и векторы fag
имеются точки fAg и векторы fag
 каждой упорядоченной паре точек A и B
каждой упорядоченной паре точек A и B
!
соответствует вектор AB
 от каждой точки fAg можно отложить любой вектор fag
от каждой точки fAg можно отложить любой вектор fag
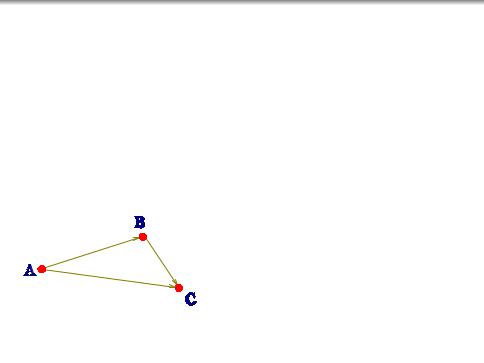
 для любых трёх точек A; B; C имеет место равенство треугольника
для любых трёх точек A; B; C имеет место равенство треугольника
! ! !
AB + BC = AC

Определение
Аффинное пространство это множество A элементов произвольной природы, называемых точками, для которого задано
а) некоторое векторное пространство V ; |
|
A • |
a |
|
б) отображение, сопоставляющее любым двум |
||||
точкам A; B 2 A некоторый вектор из V, |
A |
B |
||
обозначаемый символом ! и называемый |
• |
|||
|
AB |
|
|
• |
вектором с началом в A и концом в B. |
|
|
||
При этом требуется выполнение двух аксиом: |
A • |
|
||
9. 8A 2 A и 8a 2 V 9!B 2 A : ! |
|
B |
||
|
AB = a |
|
|
|
10. для любых трёх точек A; B; C 2 A |
|
A |
• |
|
имеет место равенство треугольника |
|
• |
• C |
|
! ! !. |
|
|
||
AB + BC = AC |
|
|
|
|
Полагая в 10. |
A = B = C , получим, ! |
. |
|
|
Полагая теперь |
AA = 0 |
|
|
|
C = A , получим, ! |
!. |
|
||
|
BA = |
AB |
|
|
Аналитическая геометрия (1-ый сем.) |
Лекция 4 |
24 сентября 2011 г. |
3 / 28 |

Векторное пространство V называется ассоциированным  с аффинным пространством A. По определению dim A = dim V.
с аффинным пространством A. По определению dim A = dim V.
Пример аффинного пространства (основной) 
Обозначается то же Rn, как и векторное.
Когда потребуется их различить, то векторное пространство (которое мы обсуждали) будем обозначать Rnвек ,
а аффинное (которое сейчас определим) будем обозначать Rnафф .
Чтобы определить аффинное пространство Rnафф , мы должны сказать
Xчто следует называть точками
Xчто векторами
Xкак паре точек сопоставляется вектор
при этом должны выполняться аксиомы 1. 10.
Аналитическая геометрия (1-ый сем.) |
Лекция 4 |
24 сентября 2011 г. |
4 / 28 |

|
|
|
|
|
|
|
|
|
|
|
x1 |
3 |
|
|
|
|
||
n |
являются столбцы |
A = |
2x2 |
|
|
|
|
|||||||||||
Точками A 2 Rафф |
6 ... |
7, |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
6xn7 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
6 |
|
|
|
7 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
4 |
|
1 |
5 |
|
|
|
|
||
|
|
|
|
|
|
|
2a2 3 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
a |
|
7. |
|
|
|
|
|||
векторами a 2 Rвек |
тоже столбцы |
a = |
6 ... |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
6an7 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
6 |
|
|
|
7 |
|
|
|
|
||
|
|
|
|
n |
|
|
|
4 |
1 |
5 |
|
|
1 |
3 |
||||
|
|
|
|
|
|
2x2 |
3 |
|
|
2y2 |
||||||||
|
|
A; B 2 Rафф ; A = 6 |
x |
|
|
|
7 |
|
|
y |
|
7 |
||||||
Каждым двум точкам |
... |
|
|
и |
B = |
6 ... |
||||||||||||
|
|
|
|
|
|
|
6xn7 |
|
|
6yn7 |
||||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
7 |
|
|
6 |
|
7 |
|
|
|
|
|
|
1 |
|
4 |
|
|
|
|
5 |
|
|
4 |
|
5 |
|
|
|
|
|
2y2 |
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
y |
|
x |
|
7. |
|
|
|
|
|
|
|
|
||
сопоставляется вектор |
a = |
! |
6 |
|
... |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
AB = |
|
|
xn7 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
6yn |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
Аналитическая геометрия (1-ый сем.) |
Лекция 4 |
24 сентября 2011 г. |
5 / 28 |
Проверять выполнение аксиом 1. 8. не требуется. Обсудим выполнение аксиом 9. 10.
9. 8A 2 A и 8a 2 V 9 ! B 2 A : |
! |
|
|
|
||||||
|
|
|
|
|
|
|
AB = a |
|
|
|
|
|
|
x1 |
3 |
|
|
|
|
a1 |
3 |
n |
; |
A = |
2x2 |
; |
|
n |
2a2 |
|||
8A 2 Rафф |
6 ... |
7 |
8a 2 Rвек ; a = |
6 ... |
7 |
|||||
|
|
|
6xn7 |
|
|
|
|
6an7 |
||
|
|
|
6 |
7 |
|
|
|
|
6 |
7 |
|
|
|
4 |
5 |
|
|
|
|
4 |
5 |
|
|
|
|
|
|
x1 |
+ a1 |
3 |
|
9 |
n |
; |
|
B = |
2x2 |
+ a2 |
: |
||
! B 2 Rафф |
|
6 |
... |
7 |
|||||
|
|
|
|
|
|
6xn |
+ an7 |
|
|
|
|
|
|
|
|
6 |
|
7 |
|
|
|
|
|
|
|
4 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
2a1 3
! 6a2 7
AB = 6 . 7 = a.
6 .. 7
4 5
an
Аналитическая геометрия (1-ый сем.) |
Лекция 4 |
24 сентября 2011 г. |
6 / 28 |
|
|
|
|
x1 |
3 |
|
|
y1 |
3 |
|
|
z1 |
3 |
|
|
|
n |
|
2x2 |
|
|
2y2 |
|
2z2 |
|
||||||
10. 8A; B; C 2 Rафф |
; A = 6 ... |
7 |
; B = |
6 ... |
7 ; |
C = |
6 |
... |
7 |
|
|||||
|
|
|
6xn7 |
|
|
6yn7 |
|
6zn7 |
|
||||||
|
|
|
6 |
7 |
|
|
6 |
|
7 |
|
6 |
|
7 |
|
|
|
|
|
4 |
5 |
|
|
4 |
|
5 |
|
4 |
|
5 |
|
|
|
|
y1 x1 |
3 |
|
z1 y1 |
z1 x1 |
3 |
||||||||
! ! ! |
|
2y2 |
x2 |
|
2z2 |
y2 3 |
2z2 |
x2 |
|||||||
() 6 ... |
|
7 |
+ |
6 |
... |
|
7 = 6 |
|
... |
|
7. X |
||||
AB + BC = AC |
|
6yn |
|
xn7 |
6zn |
|
yn7 6zn |
|
xn7 |
||||||
|
|
6 |
|
|
7 |
|
6 |
|
|
7 |
6 |
|
|
|
7 |
|
|
4 |
|
|
5 |
|
4 |
|
|
5 |
4 |
|
|
|
5 |
Аналитическая геометрия (1-ый сем.) |
Лекция 4 |
24 сентября 2011 г. |
7 / 28 |

Координаты точки в аффинном пространстве
Аффинное пространство A его элементы точки A 2 A,
V линейное (векторное) пространство ассоциированное с A; Пусть dim A dim V = n .
e1; e2; : : : ; en базис в пространстве V.
Определение
Аффинной системой координат в A называется совокупность, состоящая из точки O 2 A и векторов e1; e2; : : : ; en, образующих базис в пространстве V.
Обозначается система координат символом Oe1e2 : : : en.
В соответствии с аксиомой 9. аффинных
пространств, векторы ej |
можно откладывать |
|||||||
от любой точки, удобно отложить их от точки O. |
||||||||
8A 2 A |
A |
! |
! |
2 V (радиус-вектор) |
||||
! |
1 |
|
|
2 |
OA |
|
n, |
|
+ a2e |
+ : : : + ane |
|||||||
OA = a1e |
|
|
|
|||||
a1; a2; : : : ; an координаты точки A 2 A  в системе координат Oe1e2 : : : en.
в системе координат Oe1e2 : : : en.

Т.о., задав в аффинном пространстве A систему координат Oe1e2 : : : en,
и сопоставив каждой точке A 2 A
|
a1 |
3 |
|
2a2 |
|
столбец из её координат |
A 7 !6 ... |
7, |
|
6an7 |
|
|
6 |
7 |
|
4 |
5 |
мы получаем отображение |
A 7 !Rаффn . |
|
Это отображение является изоморфизмом
произвольного аффинного пространства A в эталонное Rnафф . Оно называется координатным изоморфизмом .
Т.о., аналогично случаю векторных пространств, произвольное n – мерное аффинное пространство Rnафф оказалось изоморфно A : A Rnафф .
Аналитическая геометрия (1-ый сем.) |
Лекция 4 |
24 сентября 2011 г. |
9 / 28 |

И, как следствие, любые два n – мерных
аффинных пространства A и B изоморфны A B .
Изоморфизм аффинных пространств A и B
одинаковой размерности можно установить непосредственно.
Для этого нужно и в пространстве A и в пространстве B
ввести системы координат и объявить соответствующими те точки, которые имеют одинаковые координаты в своих системах координат.
Полученный изоморфизм пространств A и B называется изоморфизмом по равенству координат.
Аналитическая геометрия (1-ый сем.) |
Лекция 4 |
24 сентября 2011 г. |
10 / 28 |
