Вариант №3
Задача №1
Точки
,
,
и
являются вершинами тетраэдра.
1. Поверить,
что точки
,
,
,
не лежат в одной плоскости.
2. Найти:
– объём тетраэдра;
– длину
высоты тетраэдра, опущенной из вершины
;
– расстояние
между скрещивающимися рёбрами
и
;
– уравнение
плоскости, проходящей через точки
,
,
.
Задача №2
Найти
решение системы линейных алгебраических
уравнений при всех действительных
значениях параметра
.
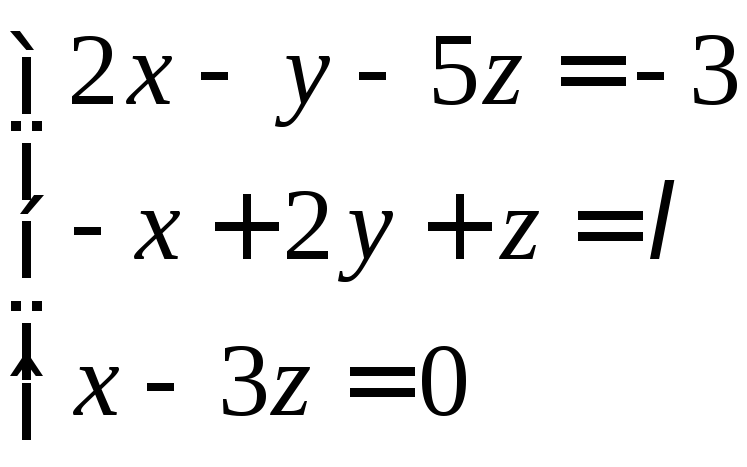Задача №3
Составить
уравнение гиперболы в канонической
системе координат, если уравнения
директрис
,
а точка
принадлежит гиперболе.
Задача №4
Вычислить пределы
а) 
;
б)
.
Задача №5
Найти производные следующих функций
а) 
;
б)
.
Задача №6
Для следующих функций провести их полные исследования средствами дифференциального исчисления и построить их графики
а)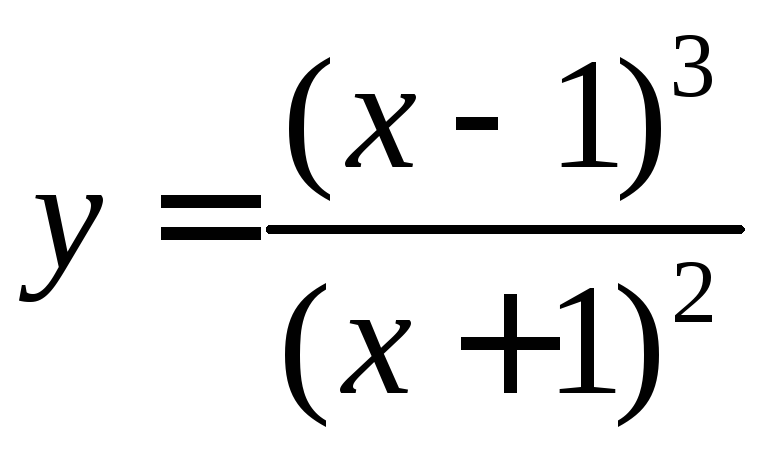 
;
б)
.
Задача №7
Исследовать на экстремум следующую функцию двух переменных
.
Задача №8
Найти экстремумы функции
при условии
.
Задача №9
Вычислить интегралы, пользуясь формулой Ньютона-Лейбница
а)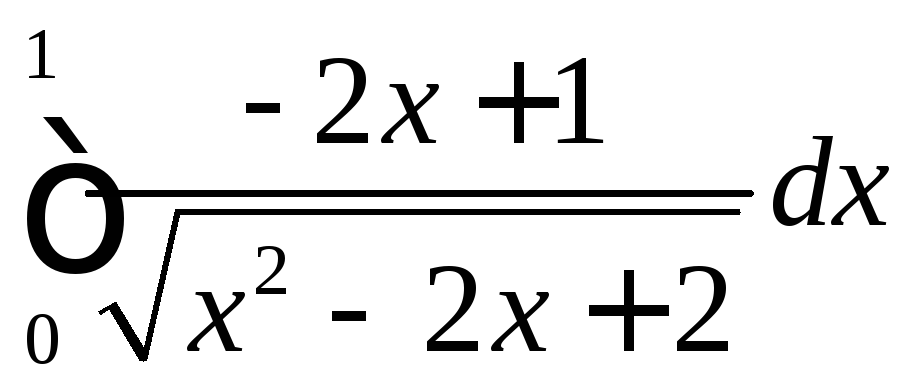 
;
б)
;
в)
.
Задача №10
Вычислить площадь, заключенную между линиями
и
.
Задача №11
Найти длину дуги кривой
,
.
Задача №12
Исследовать ряд на сходимость
.
Задача №13
Найти интервал сходимости степенного ряда и исследовать его на сходимость на концах этого интервала
.
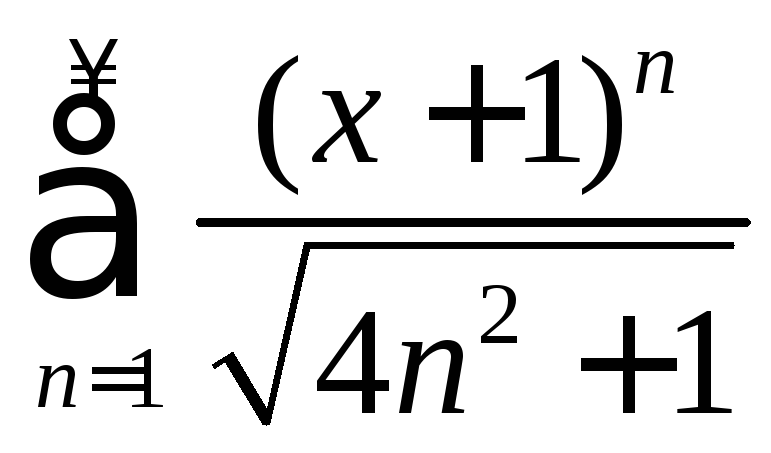Задача №14
Разложить
в степенной ряд в окрестности точки
,
функцию
.
Вариант №4
Задача №1
Точки
,
,
и
являются вершинами тетраэдра.
1. Поверить,
что точки
,
,
,
не лежат в одной плоскости.
2. Найти:
– объём тетраэдра;
– длину
высоты тетраэдра, опущенной из вершины
;
– расстояние
между скрещивающимися рёбрами
и
;
– уравнение
плоскости, проходящей через точки
,
,
.
Задача №2
Найти
решение системы линейных алгебраических
уравнений при всех действительных
значениях параметра
.
Задача №3
Составить уравнение эллипса в канонической системе координат, если расстояние между вершинами на большой полуоси равно 16, а расстояние между фокусами равно 10.
Задача №4
Вычислить пределы
а) 
;
б)
.
Задача №5
Найти производные следующих функций
а) 
;
б)
.
Задача №6
Для следующих функций провести их полные исследования средствами дифференциального исчисления и построить их графики
а) 
;
б)
.
Задача №7
Исследовать на экстремум следующую функцию двух переменных
.
Задача №8
Найти экстремумы функции
при условии
.
Задача №9
Вычислить интегралы, пользуясь формулой Ньютона-Лейбница
а) 
;
б)
;
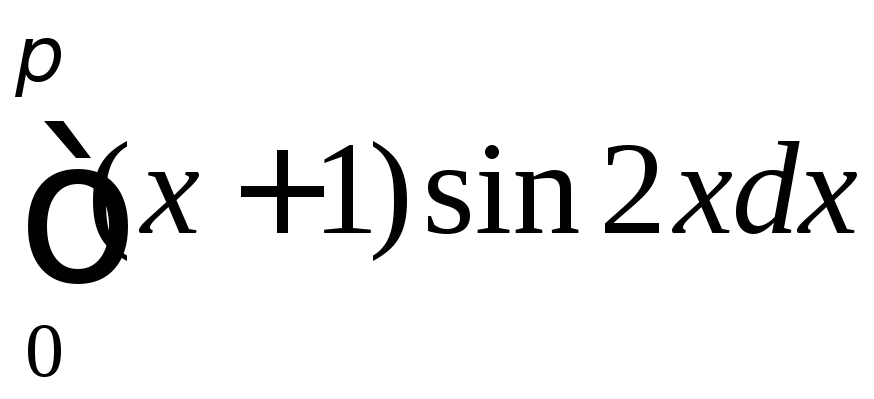в)
.
Задача №10
Вычислить площадь, заключенную между линиями
и
.
Задача №11
Найти длину дуги кривой
,
.
Задача №12
Исследовать ряд на сходимость
.
Задача №13
Найти интервал сходимости степенного ряда и исследовать его на сходимость на концах этого интервала
.
Задача №14
Разложить
в степенной ряд в окрестности точки
,
функцию
.
Вариант №5
Задача №1
Точки
,
,
и
являются вершинами тетраэдра.
1. Поверить,
что точки
,
,
,
не лежат в одной плоскости.
2. Найти:
– объём тетраэдра;
– длину
высоты тетраэдра, опущенной из вершины
;
– расстояние
между скрещивающимися рёбрами
и
;
– уравнение
плоскости, проходящей через точки
,
,
.
Задача №2
Найти
решение системы линейных алгебраических
уравнений при всех действительных
значениях параметра
.
Задача №3
Составить
уравнение эллипса в канонической системе
координат, если фокусы эллипса
,
а уравнения директрис
.
Задача №4
Вычислить пределы
а)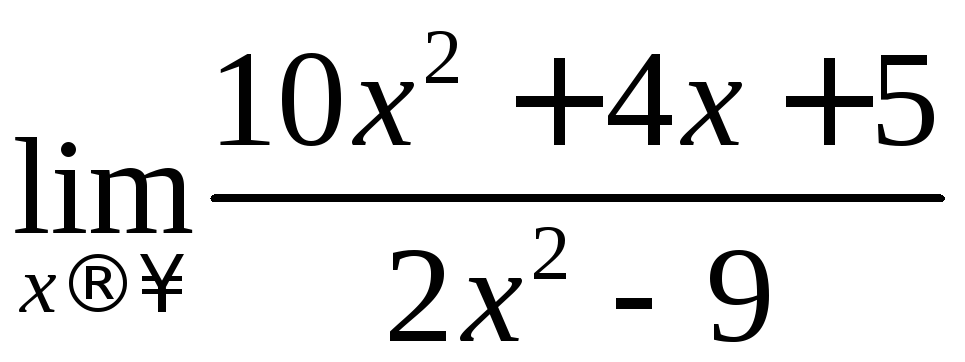 
;
б)
.
Задача №5
Найти производные следующих функций
а) 
;
б)
.
Задача №6
Для следующих функций провести их полные исследования средствами дифференциального исчисления и построить их графики
а) 
;
б)
.
Задача №7
Исследовать на экстремум следующую функцию двух переменных
.
Задача №8
Найти экстремумы функции
при условии
.
Задача №9
Вычислить интегралы, пользуясь формулой Ньютона-Лейбница
а)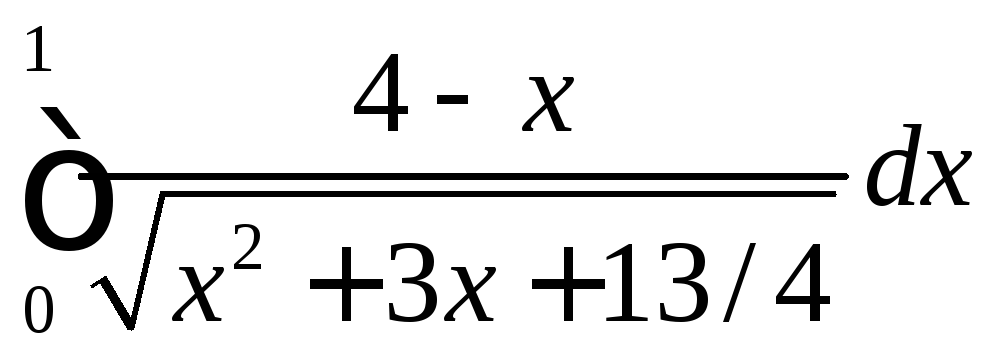 
;
б)
;
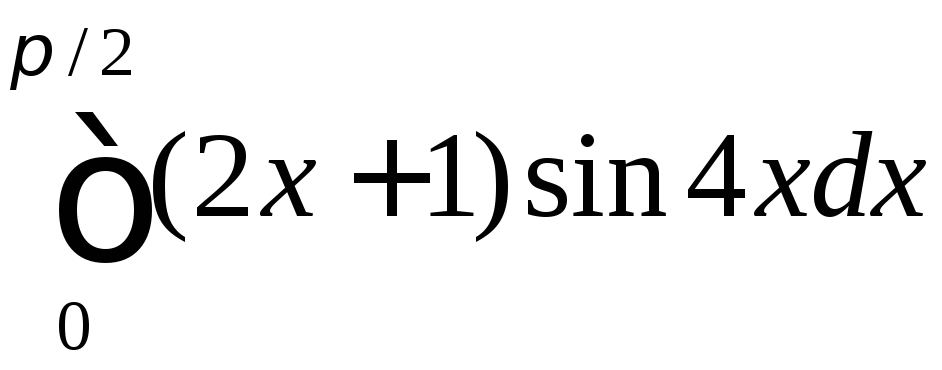в)
.
Задача №10
Вычислить площадь, заключенную между линиями
и
,
.
Задача №11
Найти длину дуги кривой
,
.
Задача №12
Исследовать ряд на сходимость
.
Задача №13
Найти интервал сходимости степенного ряда и исследовать его на сходимость на концах этого интервала
.
Задача №14
Разложить
в степенной ряд в окрестности точки
,
функцию
.