Решение

Воспользуемся интегральной теоремой Лапласа:

,

где – функция Лапласа,

, .

По условию ;;;,. Тогда:

; .

С учётом нечётности функции Лапласа , получим:

.

Задача 13

Случайная величина может принимать только два значенияи, причём. Известны вероятность возможного значения , математическое ожидание и дисперсия . Найти закон (ряд) распределения этой случайной величины [5].

Решение

Сумма вероятностей всех возможных значений дискретной случайной величины должна быть равна единице, поэтому вероятность того, чтопримет значениеравна:.

Тогда закон распределения :

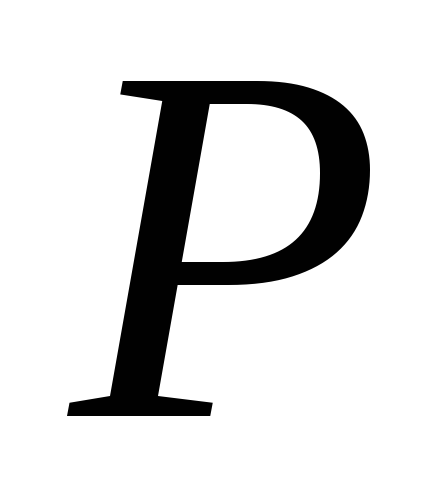
	0,6	0,4

По определению:

;

.

Напишем закон распределения :

	0,6	0,4

Найдём ,

тогда .

Имеем систему уравнений для нахождения и:

.

Решая систему, найдём: ,и,. По условию, поэтому второе решение не подходит. Тогда закон распределения дискретной случайной величины имеет вид:

	1	2
	0,6	0,4

Задача №14

Случайная величина задана функцией распределения, требуется:

1) найти плотность вероятности;

2) математическое ожидание и дисперсию ;

3) построить графики функции распределения и функции плотности распределения.

.

Решение

Найдём плотность распределения. По определению:

.

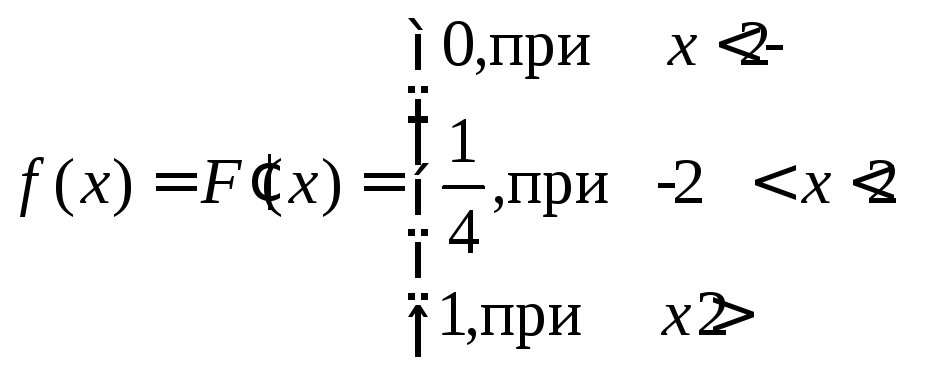Тогда

,

.

График функции распределения представлен на рисунке 6.

Рисунок 6

График функции плотности распределения представлен на рисунке 7.

Рисунок 7

Задача №15

Заданы математическое ожидание и средне квадратическое отклонениенормально распределённой величины. Найти: 1) вероятность того, чтопримет значение, принадлежащие интервалу; 2) вероятность того, что абсолютная величина отклоненияокажется меньше.

.

Решение

1) Воспользуемся формулой:

,

подставив , получим:

.

По таблицам приложения [5] находим ;. Тогда искомая вероятность равна:

.

2) Искомая вероятность находится по формуле:

.

По условию . Следовательно:

Задача №16

Провести исследование генеральной совокупности, используя выборочные данные:

2	25	3	9	11	16	2	3	23	12,5	7	26	25	9	3
11	18	26	16	12,5	7	9	2	26	25	11	3	7	11	25
25	18	16	3	7	16	18	9	18	23	9	7	26	25	16
18	9	7	11	16	23	25	26	12,5	26	7	11	7	7	11
12,5	16	18	26	25	18	11	18	25	26	16	18	25	16	18
25	23	11	16	18	25	25	23	18	11	25	16	26	25	25
18	25	23	25	23	7	23	25	16	25

1) Построить статистическое распределение выборки и гистограмму частот, полагая шаг .

2) Дать точечные оценки генеральному среднему и дисперсии.

3) Полагая, что выборка сделана из нормальной совокупности, построить доверительные интервалы для её математического ожидания и дисперсии, приняв доверительную вероятность .

4) При уровне значимости =0,01 проверить гипотезу о нормальности генеральной совокупности, используя критерий согласия Пирсона.