
- •Часть 1. Дифференциальные уравнения первого порядка
- •Глава 1. Общие сведения. Теорема о существовании и единственности решения ду 1-го порядка. Уравнения первого порядка с разделяющимися переменными
- •§ 1. Общие сведения. Теорема о существовании и единственности решения ду 1-го порядка.
- •1.1. Определение и формы записи дифференциального уравнения.
- •1.2. Определение решения ду. Поле направлений и изоклины уравнения. Задача Коши.
- •1.3. Теорема существования и единственности решения дифференциального уравнения вида для заданных начальных условий: .
- •§ 2. Уравнение 1-го порядка с разделяющимися переменными.
- •2.1. Формы записи дифференциального уравнения с разделяющимися переменными.
- •2.2. Простейшие задачи для дифференциальных уравнений 1-го порядка.
- •2.3. Решение дифференциальных уравнений 1-го порядка с разделяющимися переменными.
- •2.3.1. Решение ду 1-го порядка с разделяющимися переменными: .
- •2.3.2. Решение ду 1-го порядка с разделяющимися переменными: .
- •2.3.3. Решение ду 1-го порядка с разделяющимися переменными: .
- •2.3.4. Исследование особой точки (0,0) для ду 1-го порядка с разделяющимися переменными.
- •§ 4. Применение ду 1-го порядка с разделяющимися переменными: задачи из геометрии.
- •§ 5. Применение ду 1-го порядка с разделяющимися переменными: задачи из физики.
§ 5. Применение ду 1-го порядка с разделяющимися переменными: задачи из физики.
Задачи из физики интересны тем, что они «моделируют» процессы исследования физического явления, демонстрируют возможности математического анализа при решении физических (и инженерных!) задач. Также важно то, что общее решение в таких задачах воспринимается как общий метод решения (как расчетная формула), а частное решение – как применение решения к конкретным условиям физического процесса.
☺☺
П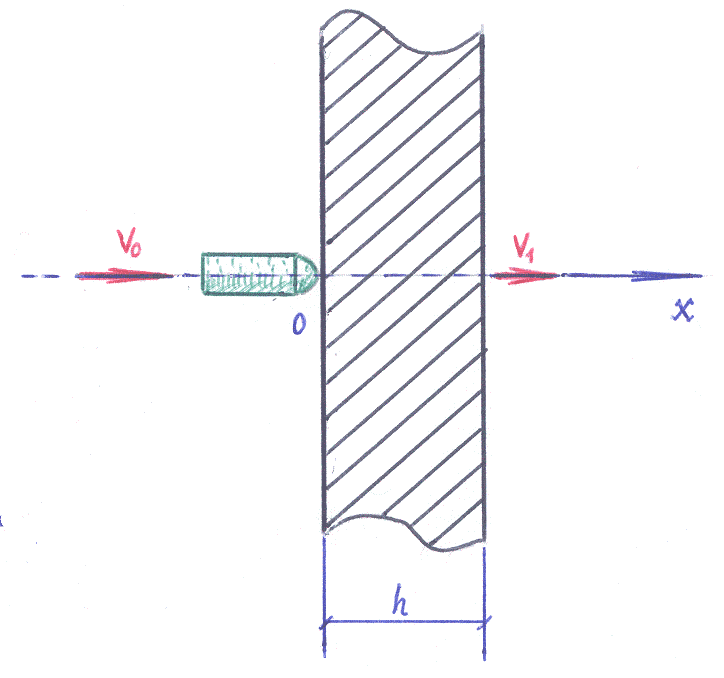 ример
1–21:
Пуля, двигаясь со скоростью
ример
1–21:
Пуля, двигаясь со скоростью ![]() =400
м/с, пробивает стену толщиной
=400
м/с, пробивает стену толщиной ![]() =20
см и вылетает из нее со скоростью
=20
см и вылетает из нее со скоростью ![]() =100
м/с. Принято, что сила сопротивления
стены пропорциональной квадрату скорости
движения пули. Необходимо найти время
=100
м/с. Принято, что сила сопротивления
стены пропорциональной квадрату скорости
движения пули. Необходимо найти время
![]() движения пули в стене.
движения пули в стене.
Решение:
Направление
оси координат ![]() и векторов скорости соответствуют
рисунку.
Учитывая, что сила сопротивления
материала стены направлена против
движения пули, в соответствии с законом
Ньютона, запишем дифференциальное
уравнение:
и векторов скорости соответствуют
рисунку.
Учитывая, что сила сопротивления
материала стены направлена против
движения пули, в соответствии с законом
Ньютона, запишем дифференциальное
уравнение: ![]() .
. ![]()
1).
Уравнение
![]() имеет тривиальное решение
имеет тривиальное решение
![]() ,
которое для нас не представляет интереса.
Считая
,
которое для нас не представляет интереса.
Считая
![]() ,
перепишем уравнение
,
перепишем уравнение
![]() в виде:
в виде: ![]() – уравнение с разделяющимися переменными.
Разделив переменные, получим уравнение:
– уравнение с разделяющимися переменными.
Разделив переменные, получим уравнение:
![]() .
. ![]()
2).
Интегрируем уравнение ![]() :
:
![]() или
или
![]() (здесь учтено свойство произвольной
постоянной величины!).
(здесь учтено свойство произвольной
постоянной величины!).
![]()
3). По
условию задачи заданы начальные условия:
в момент времени
![]() (момент касания пули с доской) скорость
пули:
(момент касания пули с доской) скорость
пули: ![]() =400
=400
![]() .
Из формулы
.
Из формулы
![]() вычисляем:
вычисляем:
![]() и записываем частное решение:
и записываем частное решение:
![]() –
закон движения пули в доске при заданных
начальных условиях.
–
закон движения пули в доске при заданных
начальных условиях.
4). По
условию задачи скорость пули в момент
вылета из доски равна ![]() =100
м/с. Используя закон движения пули в
доске, запишем равенство:
=100
м/с. Используя закон движения пули в
доске, запишем равенство:
![]() ,
откуда вычисляем:
,
откуда вычисляем:
![]() .
.
Замечание:
Рассчитать время ![]() по формуле
по формуле
![]() невозможно, так как неизвестно отношение
массы к коэффициенту сопротивления
доски
невозможно, так как неизвестно отношение
массы к коэффициенту сопротивления
доски
![]() .
.
5).
Продолжим решение задачи. Учитывая:
![]() ,
перепишем закон движения пули
,
перепишем закон движения пули
![]() в виде:
в виде:
![]() ,
или в виде:
,
или в виде:
![]() .
Для удобства, обозначим:
.
Для удобства, обозначим:
![]() и перепишем уравнение:
и перепишем уравнение:
![]() .
Разделим переменные:
.
Разделим переменные:
![]() ,
или
,
или
![]() .
.
6).
Интегрируя уравнение
![]() ,
получаем
,
получаем
![]() .
Так как в момент времени
.
Так как в момент времени
![]() координата
координата
![]() ,
можем вычислить
,
можем вычислить
![]() .
Из формулы
.
Из формулы
![]() нетрудно получить
выражение:
нетрудно получить
выражение:
![]() .
Тогда выражение
.
Тогда выражение
![]() для момента времени
для момента времени
![]() принимает
вид:
принимает
вид:
![]() .
Отсюда получаем значение коэффициента:
.
Отсюда получаем значение коэффициента:
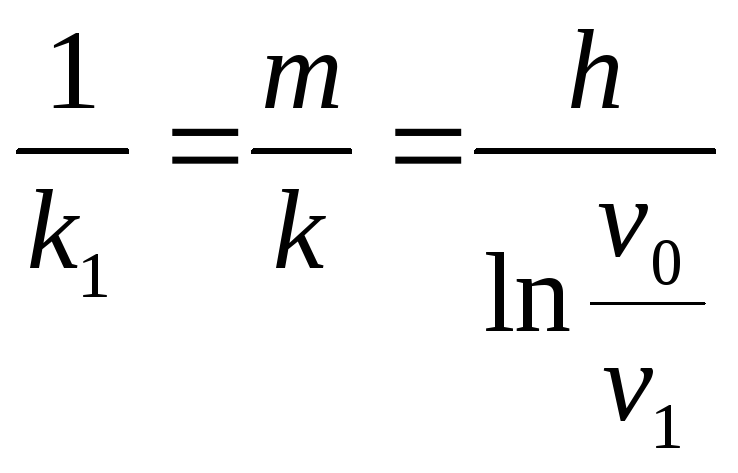 .
.
7). Теперь
можно записать формулу для вычисления
времени движения пули в стене при
заданных условиях:
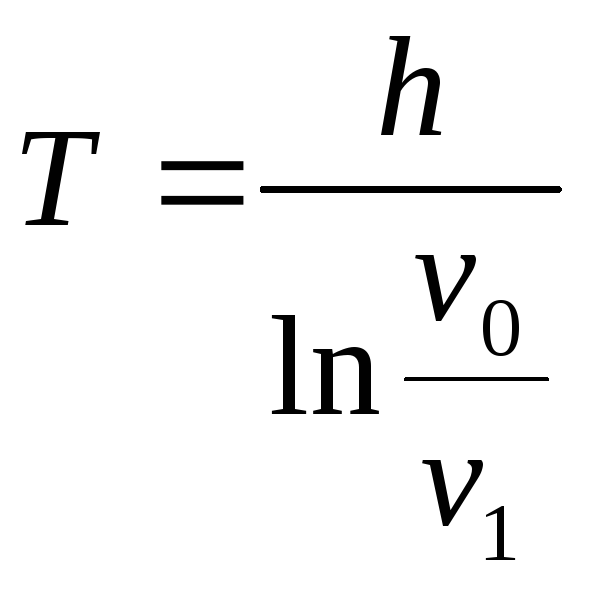
![]() .
Используя заданные скорости:
.
Используя заданные скорости: ![]() =400
м/с,
=400
м/с, ![]() =100
м/с и
=100
м/с и ![]() =20
см, получим:
=20
см, получим: ![]() .
.
Ответ:
время движения пули в стене
![]() .
.
Замечание: Рассмотренная задача представляет большой интерес, так как каждый участник её решения повторяет опыт физика, исследующего сложный процесс:
1). Выбор
модели физического процесса
![]() :
сила
:
сила ![]() пропорциональна квадрату скорости пули
есть результат физических экспериментов.
пропорциональна квадрату скорости пули
есть результат физических экспериментов.
2). Формула
для вычисления
![]() также
есть результат физических экспериментов.
Она верна для конкретной пули и стены,
причём для вычисления времени
также
есть результат физических экспериментов.
Она верна для конкретной пули и стены,
причём для вычисления времени
![]() потребовалось измерение скорости на
входе и на выходе доски.
потребовалось измерение скорости на
входе и на выходе доски.
Пример 1–22:
Пусть имеется сосуд, наполненный
жидкостью до уровня
![]() .
Известна зависимость площади
.
Известна зависимость площади
![]() поперечного сечения от высоты
поперечного сечения от высоты
![]() :
:
![]() =
=![]() .
В дне сосуда имеется отверстие, площадь
которого
.
В дне сосуда имеется отверстие, площадь
которого
![]() .
Через это отверстие жидкость вытекает.
Необходимо определить время
.
Через это отверстие жидкость вытекает.
Необходимо определить время
![]() ,
за которое уровень жидкости понизится
с начального уровня
,
за которое уровень жидкости понизится
с начального уровня
![]() до произвольного уровня
до произвольного уровня
![]() .
Также необходимо определить время
.
Также необходимо определить время
![]() полного опорожнения сосуда. Будем
считать, что скорость v
истечения жидкости из сосуда является
известной функцией
полного опорожнения сосуда. Будем
считать, что скорость v
истечения жидкости из сосуда является
известной функцией
![]() =
=![]() от уровня
от уровня
![]() жидкости в сосуде (напора).
жидкости в сосуде (напора).
Решение:
1 ).
Пусть
высота жидкости в сосуде в некоторый
момент времени
).
Пусть
высота жидкости в сосуде в некоторый
момент времени
![]() равна
равна
![]() .
Количество жидкости
.
Количество жидкости
![]() ,
вытекшее из сосуда за промежуток времени
,
вытекшее из сосуда за промежуток времени
![]() от
момента
от
момента
![]() до
до
![]() ,
можно вычислить как объём цилиндра с
площадью основания
,
можно вычислить как объём цилиндра с
площадью основания
![]() и высотой
и высотой
![]() ,
то есть:
,
то есть: ![]() =
=![]() .
.
2). С
другой стороны, можем записать величину
![]() ,
наблюдая понижение уровня жидкости в
сосуде, используя закон:
,
наблюдая понижение уровня жидкости в
сосуде, используя закон:
![]() =
=![]() .
В этом случае:
.
В этом случае:
![]() =
=![]() .
.
3).
Приравнивая два выражения для
![]() ,
получаем
дифференциальное уравнение:
,
получаем
дифференциальное уравнение:
![]() =
=![]() – уравнение с разделяющимися переменными.
Так как
– уравнение с разделяющимися переменными.
Так как
![]() ,
уравнение можно переписать в виде:
,
уравнение можно переписать в виде:
![]() =–
=–![]()
![]() .
.
4).
Интегрируя уравнение, получаем:
![]() =–
=–![]()
![]() =
=![]()
![]() .
Это значит, что полное истечение жидкости
из сосуда произойдет за время:
.
Это значит, что полное истечение жидкости
из сосуда произойдет за время:
![]() =
=![]()
![]() .
.
Замечание:
Если истечение жидкости происходит
через малое отверстие (или короткий
патрубок), то
![]() ,
где
,
где
![]() –
ускорение силы тяжести,
–
ускорение силы тяжести,
![]() –
эмпирический коэффициент (коэффициент
расхода).
–
эмпирический коэффициент (коэффициент
расхода).
Ответ:
время опорожнения сосуда до уровня h:
t=![]()
![]() .
Время полного опорожнения сосуда
потребует времени:
.
Время полного опорожнения сосуда
потребует времени:
![]() =
=![]()
![]() .
.
Пример 1–23:
Определить время опорожнения сосуда
конической формы, заполненного водой.
Форма сосуда соответствует рисунку:
![]() =0.8M;
=0.8M;
![]() =0.3M;
=0.3M;
![]() =1M;
=1M;
![]() =0.03M;
=0.03M;
![]() =0.62
(для воды).
=0.62
(для воды).
Решение:
![]()
Замечание:
Воспользуемся результатами Примере-22.
Также учтём, что при истечении жидкости
через малое отверстие (или короткий
патрубок), имеем
![]() ,
где
,
где
![]() –
ускорение силы тяжести,
–
ускорение силы тяжести,
![]() –
эмпирический коэффициент (коэффициент
расхода).
–
эмпирический коэффициент (коэффициент
расхода).
1). Для
определения площади
![]() свободной поверхности жидкости на
уровне
свободной поверхности жидкости на
уровне
![]() необходимо вычислить радиус круга на
этом уровне. Используя подобие
треугольников, выделяемых в трапеции,
этот радиус легко найти:
необходимо вычислить радиус круга на
этом уровне. Используя подобие
треугольников, выделяемых в трапеции,
этот радиус легко найти:
![]() =
=![]() =
=![]() .
. ![]()
2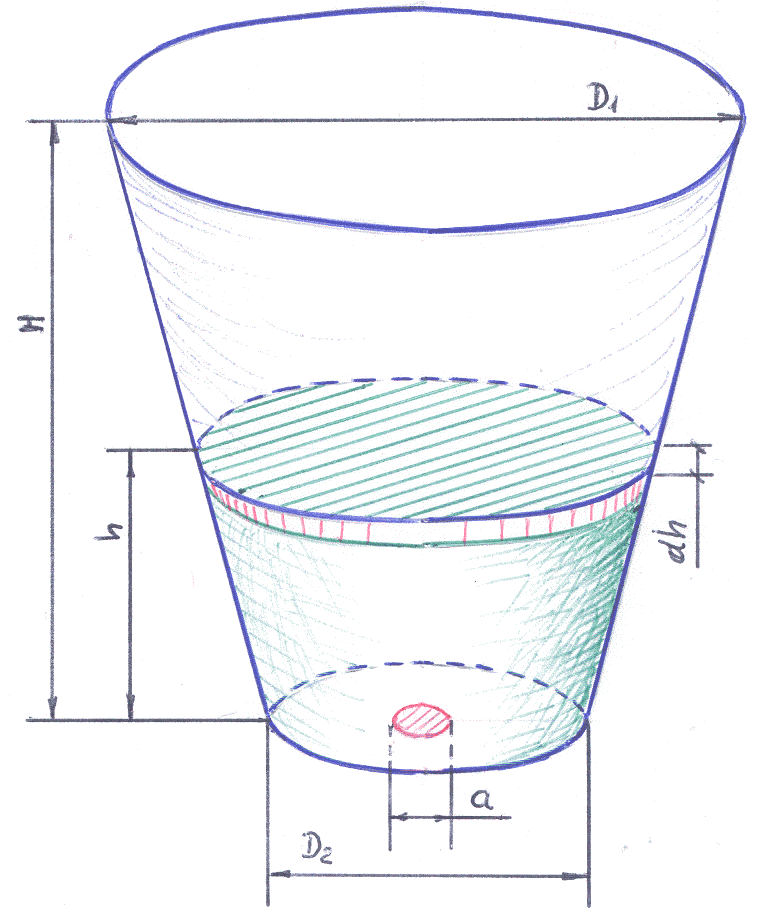 ).
Используя исходные данные, запишем
выражение для радиуса:
).
Используя исходные данные, запишем
выражение для радиуса:
![]() =
=![]() и далее для площади сечения на уровне
и далее для площади сечения на уровне
![]() :
:
![]() =
=![]() .
.
3).
Вычислим площадь отверстия, через
которое вытекает жидкость:
![]() =
=![]() .
.
4). Запишем выражение для скорости истечения жидкости для заданных условий:
![]() =
=![]()
![]() =
=![]() .
.
5). Теперь запишем формулу для вычисления времени опорожнения сосуда:
![]() =
=![]()
![]() =
=![]()
![]() .
.
Вычисляя
несложный интеграл, принимая:
![]() ,
получаем время, за которое опорожнения
сосуд опорожнился:
,
получаем время, за которое опорожнения
сосуд опорожнился:
![]() и
14c.
и
14c.
Замечание:
Если предполагается многократное
применение расчетной формулы, то удобнее
выполнить интегрирование в общем виде:
![]() =
=![]()
![]() ,
после чего подставлять в эту формулу
конкретные исходные данные.
,
после чего подставлять в эту формулу
конкретные исходные данные.
Ответ:
время истечения
![]() и
14c.
и
14c.
☻
Вопросы для самопроверки:
Имеем производную некоторой функции
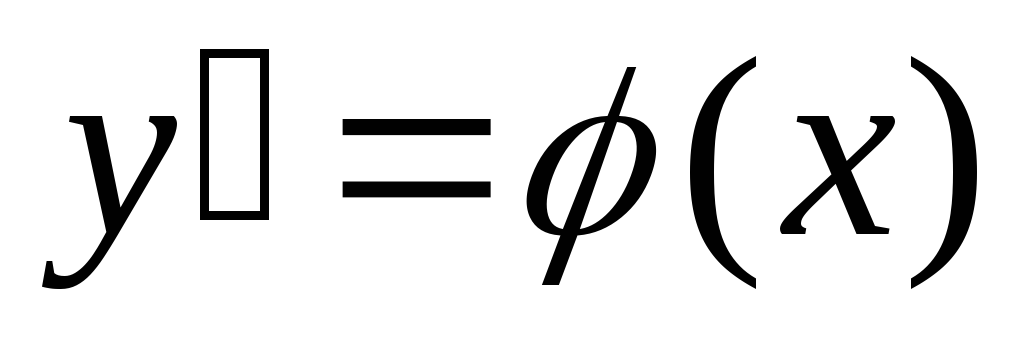 ,
что значит, функция
,
что значит, функция 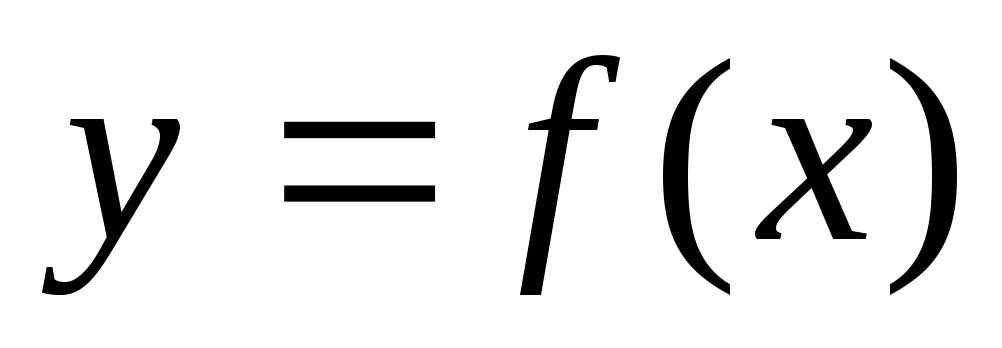 есть первообразная для функции
есть первообразная для функции 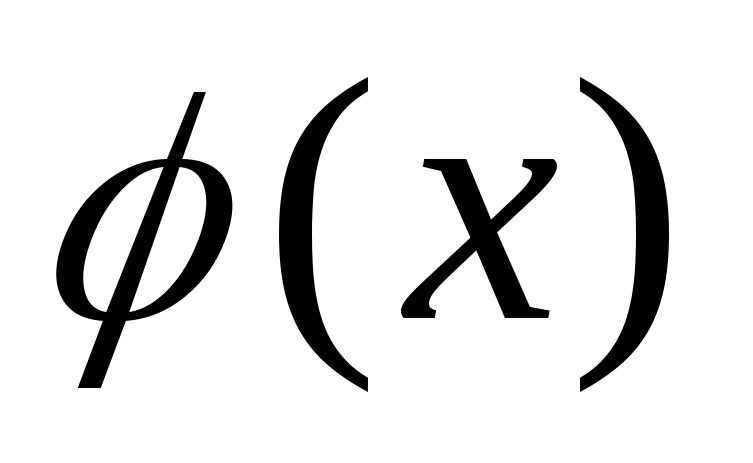 ?
?
Какое уравнение называют дифференциальным уравнением первого порядка?
Когда дифференциальное уравнение называют обыкновенным дифференциальным уравнением?
Что называют общим видом дифференциального уравнения первого порядка?
Что называют нормальной формой дифференциального уравнения первого порядка?
Что значит решить дифференциальное уравнение?
Что такое решение дифференциального уравнения?
Что называют интегральной кривой дифференциального уравнения?
Что такое поле направлений дифференциального уравнения?
Что такое изоклины дифференциального уравнения?
Что называют общим решением уравнения?
Что такое начальные условия в задачах: решить уравнение?
Что значит решить задачу Коши?
Что называют частным решением уравнения?
Уравнение задано в нормальной форме:
 .
Какие требования
предъявляет Теорема о существовании
и единственности решения
в точке
.
Какие требования
предъявляет Теорема о существовании
и единственности решения
в точке 
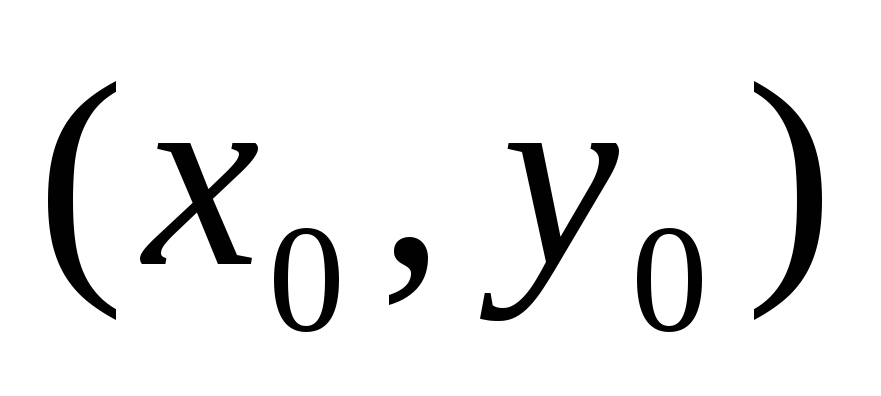 к функции
к функции
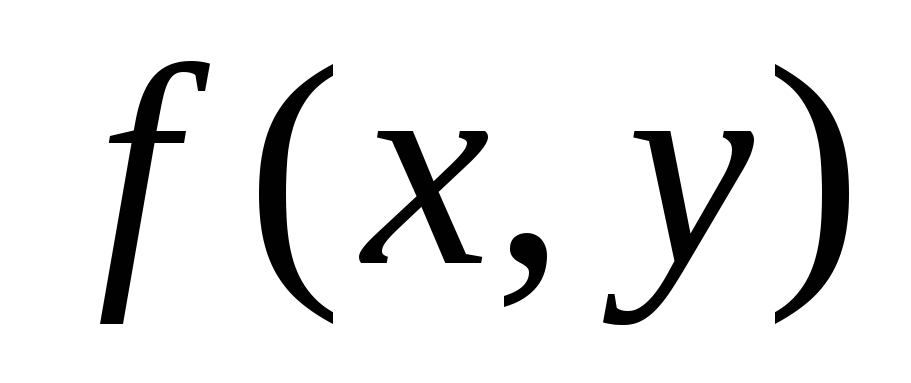 ?
?Что такое особые точки дифференциального уравнения? В каких случаях точка
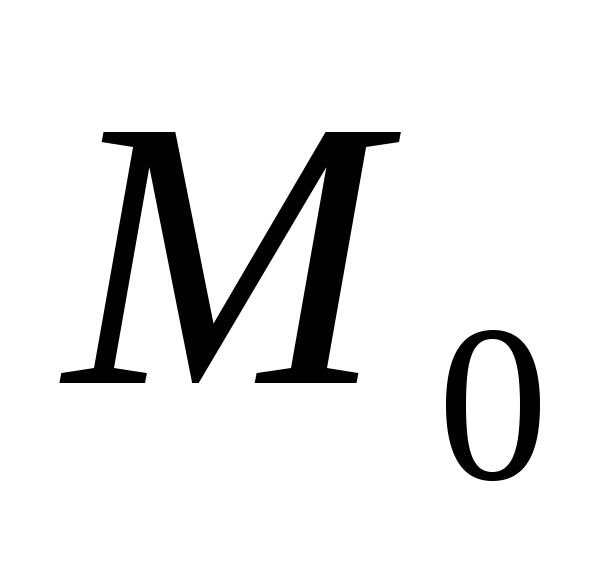
 может быть особой?
может быть особой? В каких случаях решение дифференциального уравнения называют особым решением?
Какое уравнение называют уравнением с разделёнными переменными?
Когда уравнение, записанное с использованием дифференциалов переменных
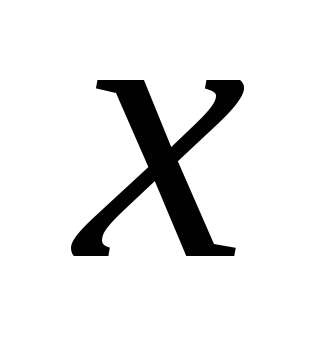 и
и  ,
называют дифференциальным уравнением
с разделяющимися
переменными?
,
называют дифференциальным уравнением
с разделяющимися
переменными?Когда уравнение, записанное с использованием нормальной формы
 ,
называют дифференциальным уравнением
с разделяющимися
переменными?
,
называют дифференциальным уравнением
с разделяющимися
переменными?Как проверить, является ли функция
 решением заданного дифференциального
уравнения 1-го порядка? Применить два
способа проверки?
решением заданного дифференциального
уравнения 1-го порядка? Применить два
способа проверки?Как построить поле направлений дифференциального уравнения без применения и с применением изоклин?
Известно общее решение
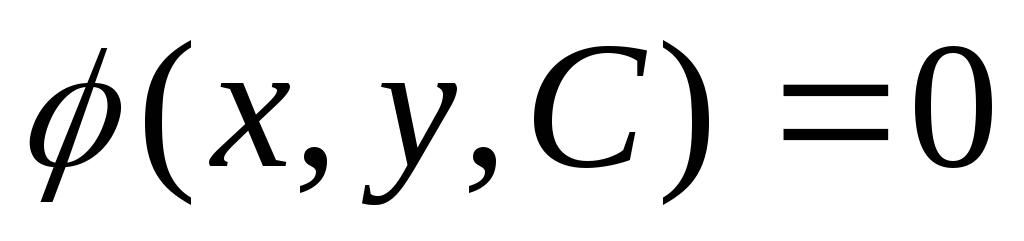 дифференциального уравнения. Как, имея
заданные начальные условия
дифференциального уравнения. Как, имея
заданные начальные условия 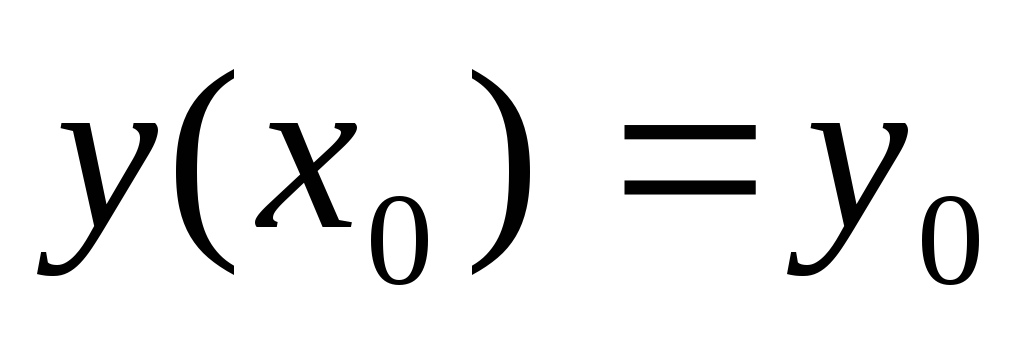 ,
выделить соответствующее частное
решение? Если короче: как решают задачу
Коши?
,
выделить соответствующее частное
решение? Если короче: как решают задачу
Коши?Пусть задано семейство кривых:
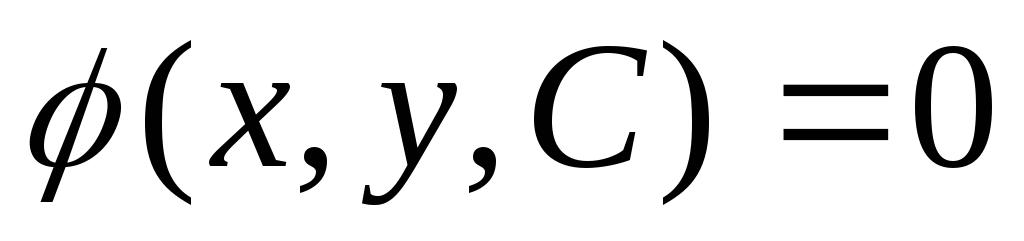 ,
где
,
где  - параметр. Каксоставитьдифференциальное уравнение,решением которогоявляется
это семейство?
- параметр. Каксоставитьдифференциальное уравнение,решением которогоявляется
это семейство?Как решают уравнение, заданное в форме
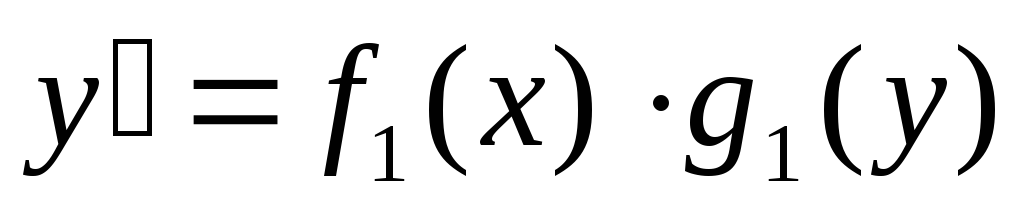 ?
?Как решают уравнение, заданное в форме
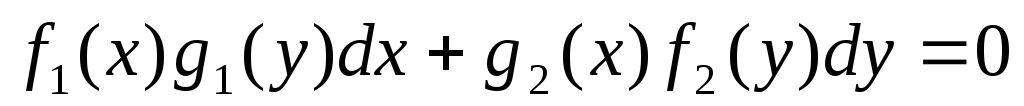 ?
?Как решают уравнение, заданное в форме
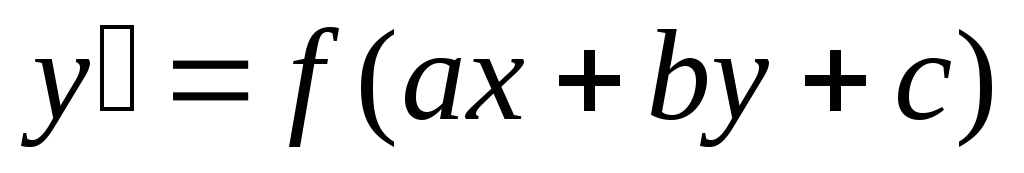 ?
?Показать в виде эскиза разновидности особой точки (0,0): узел, дикритический узел, седловина, центр.
Воспользовавшись эскизом произвольной кривой линии
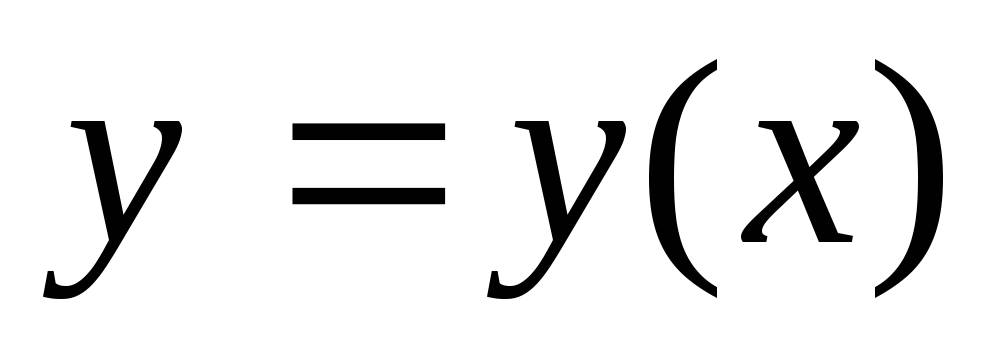 ,
назвать и показать все характерные
отрезки кривой
линии.
,
назвать и показать все характерные
отрезки кривой
линии.Как применяют дифференциальное уравнение 1-го порядка для решения геометрических задач?
Как применяют дифференциальное уравнение 1-го порядка для решения физических задач?
• ◄ ≡ ► •
