2.3.3. Решение ду 1-го порядка с разделяющимися переменными: .

Для решения уравнения, представленного в форме , будем использовать стандартный алгоритм:

1). Перепишем уравнение в виде: и примем. Учитывая, что решение уравнения, заметим, что функциятакже есть функция переменной. Дифференцируяпо переменной, получим:.

2). Учитывая результаты пункта 1, можем записать уравнение: – уравнение с разделяющимися переменными в форме. Остаётся применить стандартный алгоритмк уравнению. Получив его решение:, можем записать общее решение для исходного уравнения в виде:.

3). Если в задании указаны начальные условия: , то предполагается ещё найти частное решение (решить задачу Коши) уравнения. В точкемогут быть нарушены условия существования и единственности решения: в этом случае необходимо провести соответствующие обоснования!

4). Запишем все решения заданного дифференциального уравнения и укажем все особые точки уравнения (и особые решения), если они имеются, в Ответ.

☺☺

Пример 1–17: Решить дифференциальное уравнение: . Исследовать множество решений уравнения, применяя Теорему о существовании и единственности решения.

Решение:

1). Запись уравнения соответствует форме . Применяя общий алгоритм решения таких уравнений, обозначим:и запишем преобразованное уравнение:, то есть – уравнение с разделяющимися переменными в форме.

2). Учтём очевидное решение уравнения: , положив=0. Из тригонометрии следует, что=0, если,. Учитывая, получаем множество очевидных решений:– семейство параллельных прямых.

3). Положив , запишем уравнение в виде:. Это уравнение легко интегрируется. Его общее решение может быть записано в виде:, или.

4). Так как уравнение в записи удовлетворяет требованиям Теоремы о существовании и единственности решения, то этому же требованию удовлетворяет и исходное уравнение. Это значит, что уравнение не имеет особых точек (и особых решений). Заметим также, что множество решенийне может быть получено из выражения общего решения уравнения, ни при каких значениях постоянной.

Ответ: общее решение:, также,.

Замечание: Решение уравнения в форме трудоёмко и требует дополнительной внимательной работы, как при поиске всех решений заданного уравнения, так и при применении Теоремы о существовании и единственности решения!

☻

2.3.4. Исследование особой точки (0,0) для ду 1-го порядка с разделяющимися переменными.

Заметим, что условия Теоремы о существовании и единственности являются лишь достаточными, но не необходимыми. Поэтому особые точки ДУ следует искать среди точек разрыва функции и точек, где не существует производная , но не все такие точки обязательно особые!

Поведение интегральных кривых в окрестности особой точки бывает различным. Рассмотрим несколько Примеров, в которых особая точка (0,0) очевидна для всех используемых ДУ.

☺☺

Пример 1–18: Для дифференциального уравнения: y′= установить вид особой точки (0,0).

Р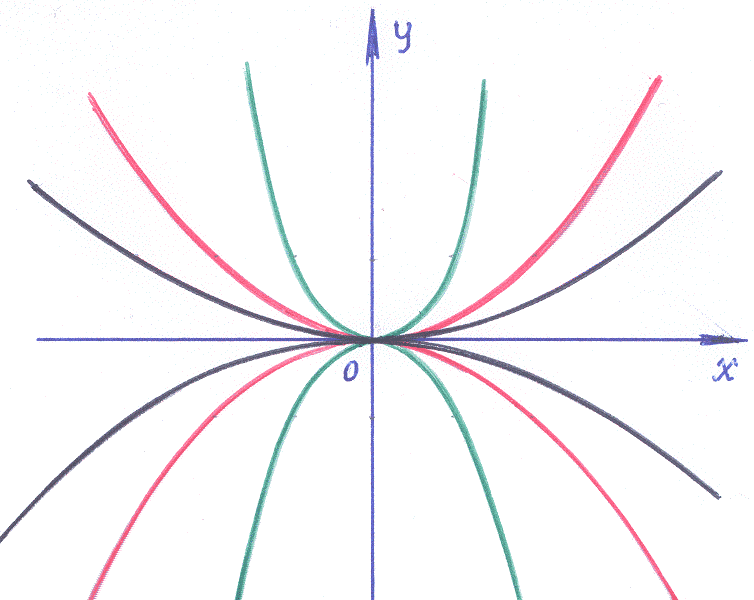ешение:

1). Учитывая исходную запись уравнения, легко заметить одно из его решений: – ось абсцисс, исключая исследуемую точку (0,0).

2). Запишем уравнение в виде: =2, удобном для интегрирования: переменные разделились. Общее решение для этого уравнения представим в виде:, которое получено в предположении, что.

3). Так как в точке (0,0) нарушены условия существования и единственности (точка (0,0) не принадлежит области определения функции правой части), то эта точка особая. По виду функции, определяющей правую часть исходной записи дифференциального уравнения: нарушение непрерывности в точке (0,0), этого можно было ожидать! По наблюдаемому рисунку множества интегральных кривых уравнения, сходящихся к точке (0,0) эту точку называют узлом.

Ответ: вид особой точки –узел.

Пример 1–19: Для дифференциального уравнения: y′= установить вид особой точки (0,0).

Решение:

1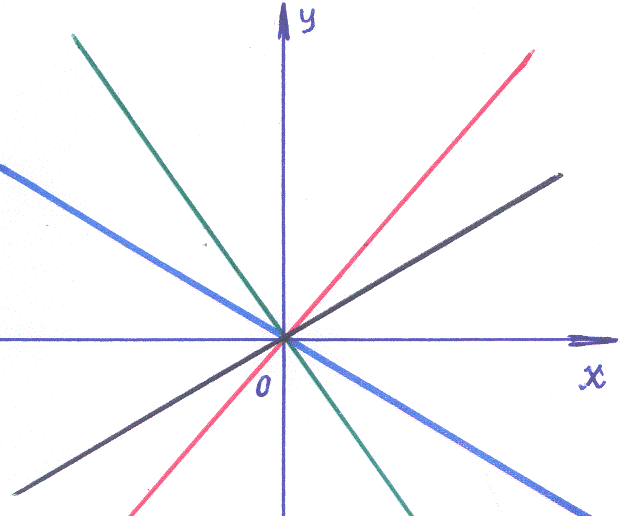). Учитывая исходную запись уравнения, легко заметить одно из его решений:– ось абсцисс, исключая исследуемую точку (0,0).

2). Запишем уравнение в виде: =, удобном для интегрирования: переменные разделились. Общее решение для этого уравнения представим в виде:, которое получено в предположении, что.

3). Так как в точке (0,0) нарушены условия существования и единственности (точка (0,0) не принадлежит области определения функции правой части), то эта точка особая. По виду функции, определяющей правую часть исходной записи дифференциального уравнения: нарушение непрерывности в точке (0,0), этого можно было ожидать! По наблюдаемому рисунку множества интегральных кривых уравнения, сходящихся к точке (0,0) эту точку называют дикритическим узлом.

Ответ: вид особой точки –дикритический узел.

Замечание: В Примере 1-18 Множество интегральных кривых в особой точке (0,0) имеют одно и то же направление: направление по оси абсцисс . В Примере-19 в особой точке (0,0) каждая интегральная кривая имеет своё направление. Для исследуемых процессов это означает, что в первом случае развитие процесса из точек, близких точке (0,0) под действием одних и тех же факторов может происходить вдоль любой из интегральных кривых. В инженерной практике таких ситуаций следует избегать: определять начальные условия процесса подальше от особых точек указанного типа!..

Пример 1–20: Для дифференциального уравнения: y′= установить вид особой точки (0,0).

Решение:

1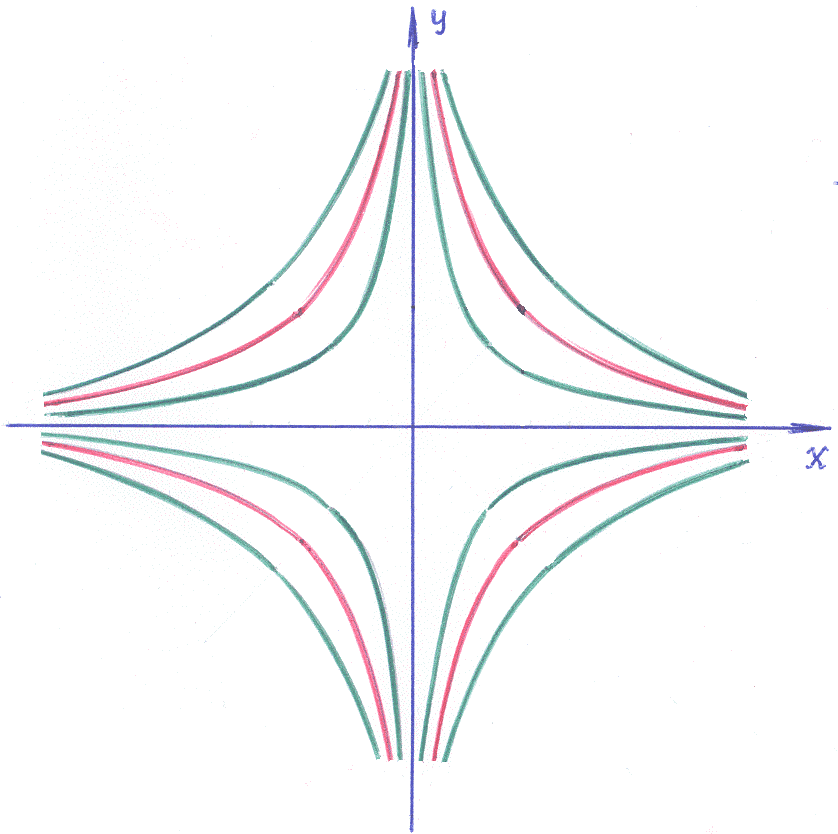). Учитывая исходную запись уравнения, легко заметить одно из его решений:– ось абсцисс, исключая исследуемую точку (0,0).

2). Запишем уравнение в виде: =, удобном для интегрирования: переменные разделились. Общее решение для этого уравнения представим в виде:, которое получено в предположении, что.

3). Так как в точке (0,0) нарушены условия существования и единственности (точка (0,0) не принадлежит области определения функции правой части), то эта точка особая: ни одна интегральная кривая не содержит точку (0,0). По виду функции, определяющей правую часть исходной записи дифференциального уравнения: нарушение непрерывности в точке (0,0), этого можно было ожидать! По наблюдаемому рисунку множества интегральных кривых уравнения, сходящихся к точке (0,0) эту точку называют седловиной.

Ответ: вид особой точки –седловина.

Пример 1–21: Для дифференциального уравнения: y′= установить вид особой точки (0,0).

Решение:

1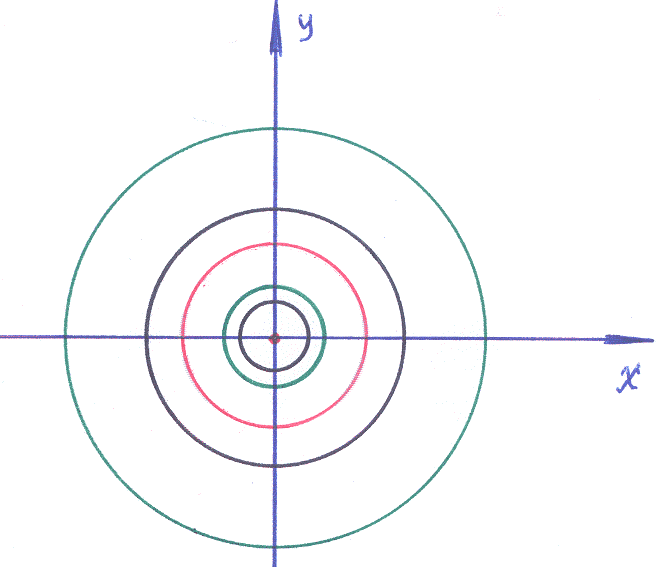). Учитывая исходную запись уравнения, легко заметить, что заданное уравнение не имеет решений очевидных: непосредственно записываемых из записи уравнения. Отметим также, что точку(0,0) не может содержать ни одна интегральная кривая!

2). Запишем уравнение в виде: , удобном для интегрирования: переменные разделились. Общее решение для этого уравнения представим в виде:, которое получено в предположении, что.

3). Так как в точке (0,0) нарушены условия существования и единственности: точка (0,0) не принадлежит области определения функции и в этой точке не существует производная, то эта точка особая. По виду функции, определяющей правую часть исходной записи дифференциального уравнения: нарушение непрерывности в точке (0,0), этого можно было ожидать! По наблюдаемому рисунку множества интегральных кривых уравнения, сходящихся к точке (0,0) эту точку называютцентром.

Ответ: вид особой точки –центр.

☻