Часть 1. Дифференциальные уравнения (ду) 1-го порядка.
ЗАНЯТИЕ 1. Основные понятия. Теорема существования и единственности ДУ 1-го порядка. Уравнения первого порядка с разделяющимися переменными.
|
Ауд. |
Л-2, Гл. 10 |
№ 1, 4, 9, 16, 26, 31, 41, 43, 167. |
9 |
☺ ☻ ☺
Основные понятия:
1. Дифференциальным уравнением (ду) называют равенство, содержащее независимые переменные, искомую функцию и её производные (или дифференциалы).
2. Решить ду – значит найти все его решения!
3. Решение ду – любая функция, которая, будучи подставлена в исходную запись уравнения, обращает его в тождество!
••• ≡ •••
Пример
1–1:
Показать, что при любом действительном
значении параметра
заданная функция
является решением ДУ:
. (1)
Решение:
1).
Разделим уравнение на
.
Получаем уравнение в виде:
. (2)
2).
Для нахождения производной заданной
функции вспомним:
,
так как имеем:
-
табличный интеграл!
Тогда:
=
.
3).
Подставим заданную функцию
и ее производную
в уравнение (2), которое равносильно
исходному уравнению (1): 
→ тождество.
4). Это значит, что заданная функция является решением заданного уравнения.
Ответ: заданная функция является решением заданного уравнения.
Пример
2–4:
В заданном семействе:
выделить уравнение кривой, удовлетворяющей
приведенному начальному условию:
.
Решение:
1).
Выделить из семейства кривых кривую,
которая проходит через точку (0,1) – это
значит вычислить значение произвольной
постоянной
,
при условии, что
=0,
=1.
2).
Подставим
=0,
=1
в выражение семейства:
,
откуда
=1.
3).
Тогда уравнение кривой семейства,
проходящей через точку (0,1):
.
Ответ:
уравнение
кривой:
.
Пример
3–9:
Составить дифференциальное уравнение
семейства парабол:
. (1)
Решение:
1). Преобразуем
выражение семейства (известная операция
выделения полного квадрата):
.
При непрерывном изменении параметра
ось параболы
смещается влево при значении параметра
,
вправо при значении
;
одновременно вершина параболы движется
по параболе
.
2).
Вычислим производную
для заданного семейства:
.
(2)
3).
Для получения дифференциального
уравнения нужно исключить параметр
из выражения (1)
или из выражения (2):
а)
умножив выражение (2) на
,
получим уравнение
=[учтём
(1)]
=
;
б)
получено дифференциальное уравнение:
=
.
Ответ:
ДУ для семейства парабол
=
.
Пример
4–16:
Методом изоклин построить приближенно
семейство интегральных кривых для
дифференциального уравнения:
.
Р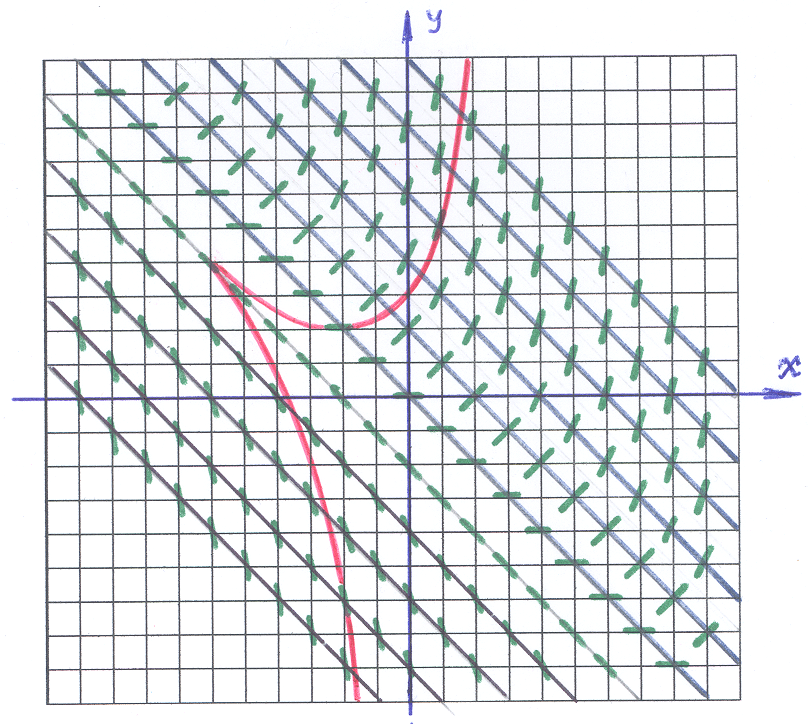
ешение:
1). Уравнение
изоклин для заданного дифференциального
уравнения получается из исходного
уравнения приравниванием
=
.
В нашем случае каждая изоклина – это
прямая:
=
.
На рисунке изоклины выделены «синим»
цветом. На каждой изоклине черточка
(«зеленая») отражает конкретное
значение
,
определяющее изоклину, то есть: на
каждой изоклине наклон черточки один
и тот же.
2). Черточки играют роль «железных опилок» в опытах по физике: они показывают направление «поля». Возникает «зрительный образ», который определяет «присутствие некоторой кривой», касательные к которой мы и видим. Это и есть приближенно выделяемая «интегральная кривая» (одна из них выделена «красным» цветом), то есть «решение» заданного ДУ.
Ответ: интегральная кривая представлена на рисунке.
Пример
5–26:
Решить дифференциальное уравнение:
. (1)
Решение:
1).
Прежде всего, отметим, что исходное
уравнение (1) не может иметь решения в
виде
,
в частности в виде функции
.
Это значит, что дифференциал
не может быть равным 0. В то же время,
функция
=0
есть решение уравнения (1).
2).
Умножим исходное уравнение (1) на
дифференциал
.
Уравнение (1) перепишем в дифференциальной
форме: 
.
(2)
3).
Нетрудно заметить, что уравнение (2) есть
уравнение с разделяющимися переменными.
Так как решение
уже учтено, теперь примем, что
и перепишем уравнение (2) в виде: 
+
=0. (3)
4). Используя простейшие приёмы вычисления неопределённых интегралов, проинтегрируем уравнение (3). При получении общего решения уравнения (3) применим два принципиально разных способа использования произвольной постоянной величины:
→
или
.
(4)
→
или
.
(5)
Замечания: 1. При получении выражений (4) и (5) принципиальным было применение условия y≠0. При получении записи (5) также необходимо потребовать выполнения условия C≠0!..
2. Использование записи (5) удобнее в случае решения задачи Коши: вычисление постоянной C совсем просто, при использовании (4) пришлось бы применять логарифмы!.. Если общее решение уравнения воспринимать как совокупность кривых, то записи эквиваленты!..
Ответ:
общее решение ДУ
;
хотя при получении общего решения
произвольная постоянная величина
не должна принимать значение 0, формально
из него можно получить решение исходного
уравнения
при значении
.
Пример
6–31:
Решить дифференциальное уравнение:
. (1)
Решение:
1).
Прежде всего, отметим, что исходное
уравнение (1) имеет решения в виде функций:
– прямые, параллельные оси
,
и
,
то есть ось
.
2).
Теперь воспользуемся тем, что переменные
в уравнении разделяются. Так как решения
и
учтены, примем теперь
и
,
и запишем уравнение в виде:
. (2)
3). Используя простейшие приёмы вычисления неопределённых интегралов, проинтегрируем уравнение (2). Получаем общее решение уравнения (2):
→
.
(3)
Ответ:
общее решение ДУ
;
в данном случае решение исходного
уравнения
можно
получать из общего при значении
=0;
решения
также формально можно получать из общего
решения.
Пример
7–41:
Решить дифференциальное уравнение:
. (1)
Решение:
1).
Преобразуем заданное уравнение к виду:
=
.
Известно, что такое уравнение легко
приводится к уравнению с разделяющимися
переменными!
2).
Примем
и вычислим производную
,
то есть
.
В нашем случае получаем
,
что есть уравнение с разделяющимися
переменными!
3).
Уравнение
имеет решение в виде функции:
.
Учитывая обозначение
,
запишем решение
– прямая линия.
Замечание: Увидеть
решение
непосредственно из исходного уравнения
было бы совсем непросто!
4).
Пусть теперь
.
Запишем уравнение
в виде:
,
или (для удобства!) в виде:
. (2)
5).
Интегрирование уравнения (2) не составит
труда, даже на начальном этапе освоения
неопределённого интеграла 
→
. (3)
Ответ:
общее решение ДУ
;
в данном случае решение
можно получить формально из общего при
значении
=0;
запишем общее решение и в виде
,
из которого решение
получается из общего при значении
=0.
Пример
8–43:
Решить дифференциальное уравнение:
,
. (1)
Решение:
1).
Прежде всего, отметим, что исходное
уравнение (1) имеет решение:
–
ось
.
2).
Переменные в уравнении разделяются.
Так как решение
уже учтено, примем теперь
,
и запишем уравнение в виде: 
. (2)
3).
Интегрирование уравнения (2) не составит
труда, даже на начальном этапе освоения
неопределённого интеграла 
→
. (3)
4).
Используя начальные условия
,
вычисляем:
и получаем
частное решение уравнения:
–
гипербола, её график включает две
ветви. Начальные условия выделяют правую
ветвь гиперболы!
Ответ:
–
частное решение ДУ: правая ветвь
гиперболы.
Пример
9–167:
Найти уравнение кривой линии, проходящей
через точку
,
если длина отрезка полуоси
абсцисс, отсекаемого её касательной,
равна квадрату абсциссы точки касания.
Решение:
В
Главе 1 пособия по теории Дифференциальных
уравнений в § 3 получено выражение:
=
– длина отрезка полуоси абсцисс,
отсекаемого её касательной; абсциссу
точки касания обозначим
=
.
С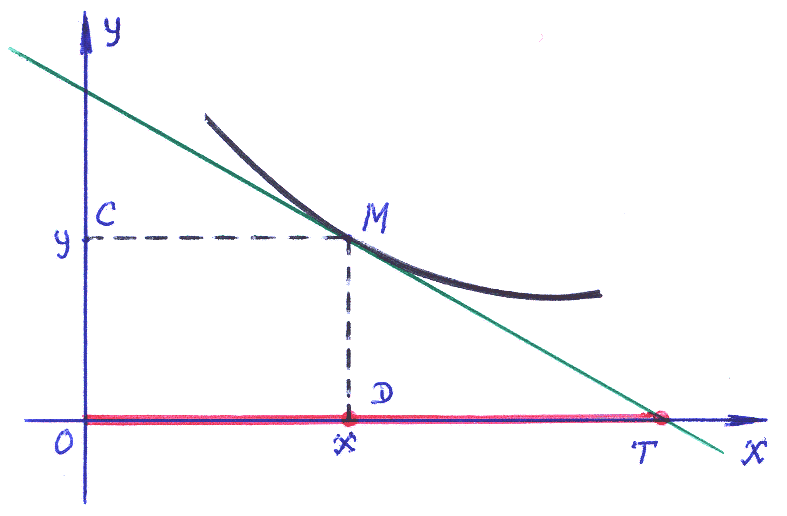
огласно
условию задачи и в соответствии с
принятыми обозначениями необходимо
рассмотреть два случая:
▪ Случай-1:
; (1)
▪ Случай-2:
. (2)
Случай-1.
1).
Запишем дифференциальное уравнение
(1) в виде:
– уравнение с разделяющимися переменными,
обозначим его
.
2).
Из записи
нетрудно выделить решения:
–
ось
,
–
прямая, параллельная оси
и
–
ось
.
Эти решения не отражают существа
поставленной геометрической
задачи.
3).
Пусть теперь
и
.
Перепишем уравнение
в виде
=
–
переменные разделились. Интегрируем
уравнение:
–
=
=
.
Используя табличные интегралы и исключая
логарифмы, можем записать общее решение:
=
,
или
=
. (3)
4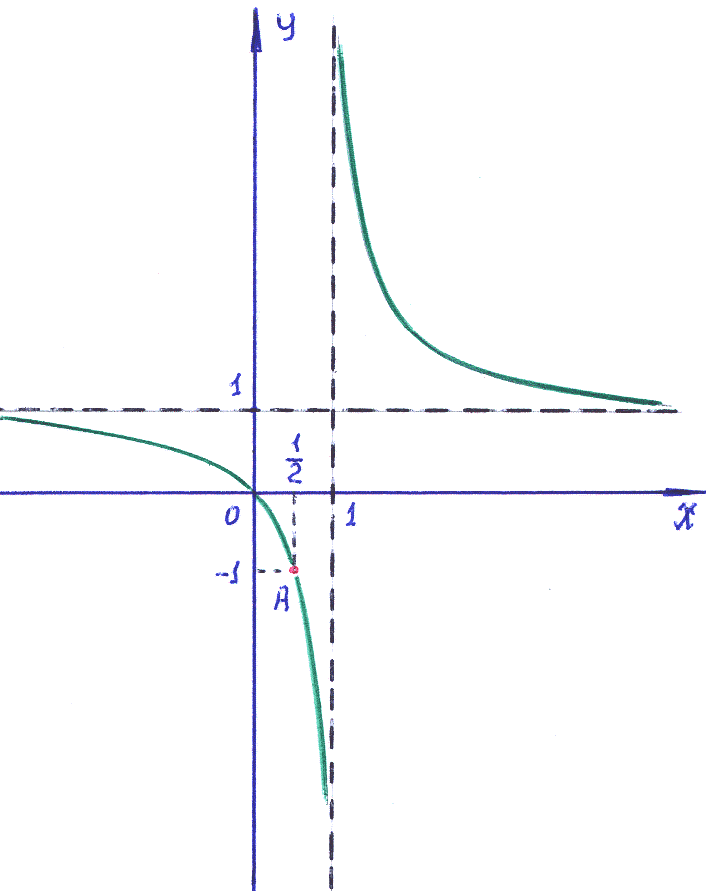
).
Из записи
общего решение дифференциального
уравнения следует, что это семейство
гипербол.
Для
иллюстрации присвоим произвольной
величине
значение 1. Известно, что график функции
=
может быть получен, если к простейшей
гиперболе
применить преобразования:
Сместить
график вправо на 1, лучше сместить ось
на 1 влево.
Сместить
график вверх на 1, лучше сместить ось
на 1 вниз.
Учёт
параметра
в записи (3) может быть отмечен возможными
действиями: сжатие-растяжение вдоль
оси
,
вращение вокруг оси
и движение вверх-вниз.
Так
как по условию задачи кривая должна
проходить через точку
,
то используя выражение общего решения
(3), получаем значение
.
Именно для этого случая применён рисунок.
Учитывая условие задачи, заметим, что
решением является ветвь гиперболы,
проходящая через точку
.
Случай-2.
1).
Запишем дифференциальное уравнение
(2) в виде:
– уравнение с разделяющимися переменными,
обозначим его
.
2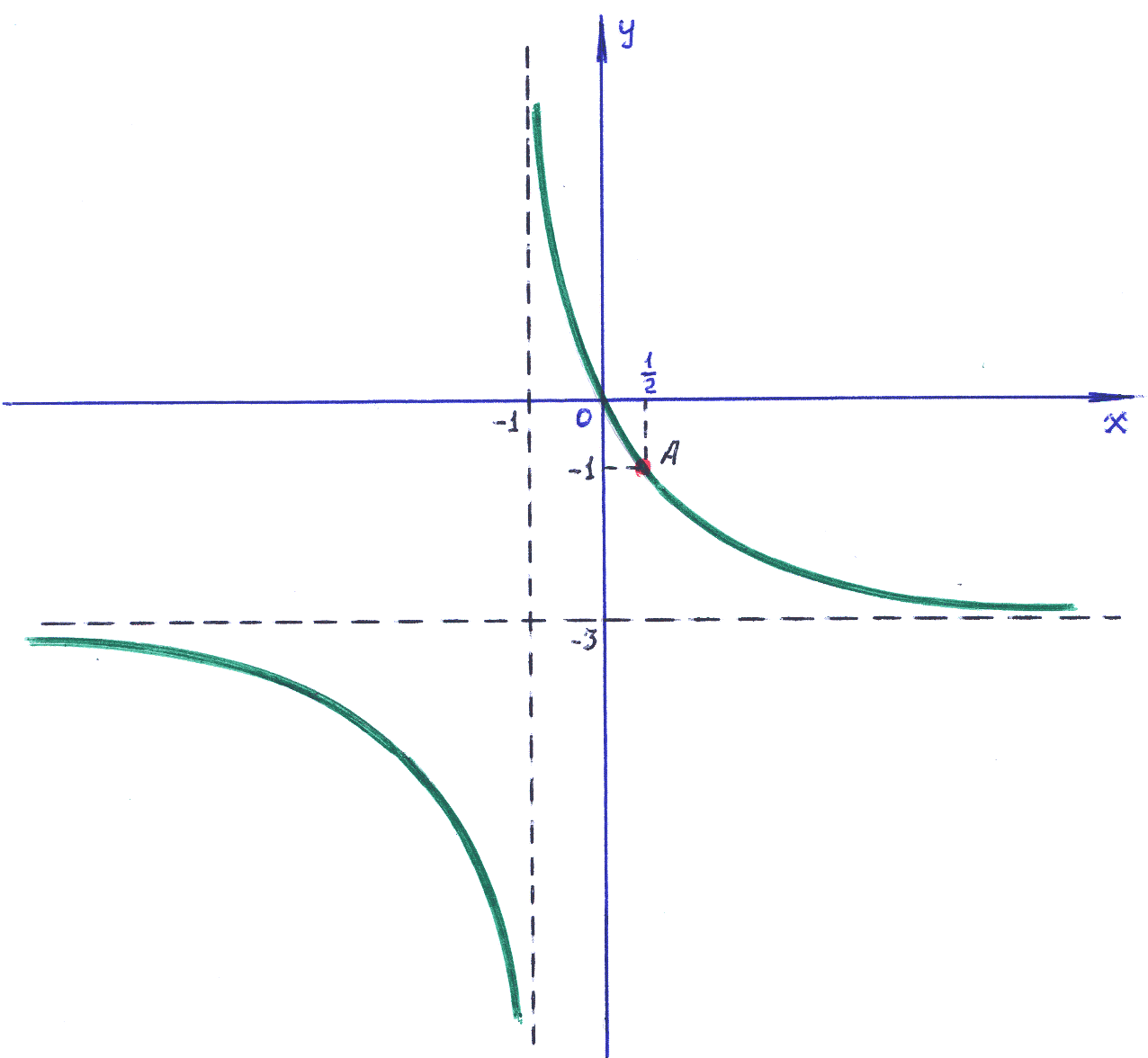
).
Из записи
нетрудно выделить решения:
–
ось
,
–
прямая, параллельная оси
и
–
ось
.
Эти решения не отражают существа
поставленной геометрической
задачи.
3).
Пусть теперь
и
.
Перепишем уравнение
в виде
=
–
переменные разделились. Интегрируем
полученное уравнение:
–
=
=
.
Используя табличные интегралы и
исключая логарифмы, можем записать
общее решение:
=
,
или
=
. (4)
4). Из записи общего решение дифференциального уравнения следует, что это семейство гипербол.
Для
иллюстрации присвоим произвольной
величине
значение –3.
Известно, что график функции
=
может быть получен, если к простейшей
гиперболе
применить преобразования:
Сместить
график влево на 1, лучше сместить ось
на 1 вправо.
Сместить
график вниз на 3, лучше сместить ось
на 3 вверх.
Учёт
параметра
в записи (4) может быть отмечен возможными
действиями: сжатие-растяжение вдоль
оси
,
вращение вокруг оси
и движение вверх-вниз.
Так
как по условию задачи кривая должна
проходить через точку
,
то используя выражение общего решения
(4), получаем значение
.
Именно для этого случая применён рисунок.
Учитывая условие задачи, заметим, что
решением является ветвь гиперболы,
проходящая через точку
.
Ответ:
Случай-1:
=
–
общее решение и частное:
=
.
Случай-2:
=
–
общее решение и частное:
=
.
•• ☻☻ ••
Вопросы для самопроверки:
-
Какое уравнение называют дифференциальным?
-
Как определить порядок ДУ?
-
Что значит - решить дифференциальное уравнение?
-
Что такое решение ДУ, частное решение ДУ?
-
Что такое общее решение ДУ?
-
Что значит решить Задачу Коши?
-
Что такое семейство кривых?
-
Как построить уравнение, решением которого является заданное семейство кривых?
-
Каковы стандартные формы ДУ с разделяющимися переменными и их решение?
Задачи для самоподготовки:
Пример
C1–1:
В заданном семействе:
выделить уравнение кривой, удовлетворяющей
приведенному начальному условию:
.
Ответ:
.
Пример
C1–2:
Решить дифференциальное уравнение:
.
Ответ:
.
Пример
C1–3:
Решить дифференциальное уравнение:
.
Ответ:
.
Пример
C1–4:
Решить дифференциальное уравнение:
.
Ответ:
.
Пример
C1–5:
Решить дифференциальное уравнение:
.
Ответ:
.
Пример C1–6: Найти уравнение кривой, проходящей через точку (1,2), если её подкасательная вдвое больше абсциссы точки касания.
Ответ:
и
.
•• ☻☻ ••
ЗАНЯТИЕ 2. Уравнения первого порядка с разделяющимися переменными. Систематизация и закрепление знаний.
|
Ауд. |
Л-2, Гл. 10 |
№ 3, 6, 17, 23, 25, 30, 38. |
7 |
☺ ☻ ☺
Замечание: При выполнении Задания необходимо руководствоваться основными понятиями, представленными в начале Занятия 1.
••• ≡ •••
Пример
1–3:
Показать, что при любом действительном
значении параметра
заданная функция
является решением ДУ:
. (1)
Решение:
1).
Разделим уравнение (1) на
:
. (2)
2).
При нахождении производной заданной
функции учтем, что функция
в нашем примере задана неявно.
Дифференцируем заданную функцию по x;
учитывая
:
=[учтём,
что
]=
. (3)
Применяя
тождественные преобразования (3), получим:
. (4)
3). Подставив в уравнение (2) левую часть равенства (4), получаем очевидное тождество:
4).
Это значит, что заданная (неявная) функция
является решением уравнения (1).
Ответ: заданная функция является решением заданного уравнения.
Пример
2–6:
В заданном семействе
выделить уравнение кривой, удовлетворяющей
приведенному начальному условию:
=
–1.
Решение:
1).
Выделить из семейства кривых кривую,
которая проходит через точку
– это значит вычислить значение
,
при условии, что
=0,
=
–1.
2).
Подставим
=0,
=
–1 в выражение семейства:
,
откуда
=
–3.