2.2. Простейшие задачи для дифференциальных уравнений 1-го порядка.

Хотя в настоящем параграфе как объект исследования назван тип дифференциальных уравнений с разделяющимися переменными, рассматриваемые ниже простейшие задачи мы будем применять ко всем изучаемым типам ДУ 1-го порядка. Решение каждой из рассматриваемых Задач представлено в виде общего алгоритма и сопровождается Примерами, в которых не предполагается, что все они должны использовать только уравнениями с разделяющимися переменными!

Задача-1. Задано дифференциальное уравнение в одной из форм записи уравнения с разделяющимися переменными. Для общего случая запишем его в форме: . Нужно проверить, является ли функция переменной решением заданного уравнения. Заметим, функция может быть задана как в явной, так и в неявной форме.

Решение:

1). Пусть функция задана в явной форме: . Вычислив производную , подставим в уравнение и . Если получим , то функция есть решение заданного уравнения, в противном случае не является решением заданного уравнения.

2). Пусть функция задана в неявной форме: . Продифференцировав это выражение по переменной , получим: , откуда . Подставим это выражение в дифференциальное уравнение. Если получим 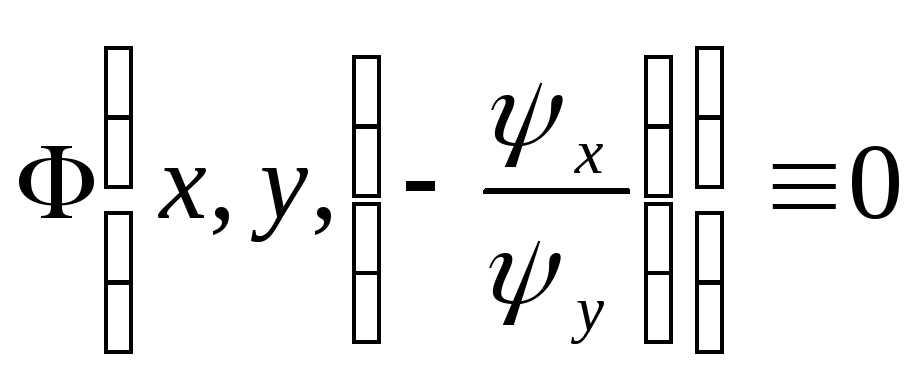, то неявная функция есть решение заданного уравнения, в противном случае не является решением заданного уравнения.

Ответ: получены общие алгоритмы решения Задачи-1.

☺☺

Пример 1–05: Показать, что при любом действительном значении параметра заданная функция является решением ДУ: .

Решение:

1). Принимая, что , разделим заданное дифференциальное уравнение на . Получаем уравнение в виде: .

2). Вычислим производную заданной функции: . Используя правило дифференцирования сложной функции, запишем: . Тогда производной заданной функции: .

3). Подставим заданную функцию и ее производную в уравнение , получим выражение: . Это значит, что функция есть решение заданного уравнения.

Ответ: доказано.

Пример 1–06: Показать, что при любом действительном значении параметра заданная функция является решением ДУ: .

Решение:

1). Принимая, что , разделим заданное дифференциальное уравнение на . Получаем уравнение в виде: .

2). Вычислим производную заданной неявной функции: . Используя выражение заданной функции, запишем: , откуда, применяя тождественные преобразования, получаем: .

3). Подставим выражение в уравнение , получим выражение: . Это значит, что функция есть решение заданного уравнения.

Ответ: доказано.

Замечание: Решение Задачи-1 в случае неявного задания функции: осуществляется подстановкой в дифференциальное уравнение найденного выражения для производной , с учетом задающего неявную функцию выражения.

☻

Задача-2. Задано ДУ в одной из форм записи уравнения с разделяющимися переменными. Нужно построить поле направлений без применения и с применением изоклин. Использование поля направлений для проверки – явная функция или неявная функция может быть решением заданного ДУ, или не может.

Решение:

1). Определение и принципы построения поля направлений с применением изоклин рассмотрено в § 1 (разделе 1.2). Примеры 1-01 и 1-02 иллюстрируют построение изоклин для заданных дифференциальных уравнений.

2). Используя понятие поля направлений, проверить, является ли функция решением заданного дифференциального уравнения.

Ответ: получены общие алгоритмы решения Задачи-2.

☺☺

Пример 1–07: Задана функция , где параметр. Является ли эта функция решением дифференциального уравнения: .

Решение:

1). На плоскости выберем точку (1,2). Используя уравнение , вычислим направление поля в точке → .

2). Учитывая координаты точки , из выражения вычислим значение параметра: =2. Значит кривая, содержащая точку , определяется функцией: . Вычислим производную этой функции: . Используя выражение: , вычислим направление касательной к кривой в точке : угловой коэффициент касательной в этой точке =1. Так как , то есть не совпадает с направлением поля, определяемым дифференциальным уравнением, то выражение не есть решение заданного дифференциального уравнения!

Ответ: не является.

Замечание: В рассмотренном примере мы фактически решили Задачу-1, но использовали средства, отнесённые к Задаче-2, и получили существенное уменьшение трудоёмкости вычислений. Для случая неявной функции: выигрыш в трудоёмкости будет ещё большим!

Пример 1–08: Задана функция , где параметр. Является ли эта функция решением дифференциального уравнения: .

Решение:

1). На плоскости выберем точку (2,1). Используя заданное уравнение, вычислим направление поля в точке → .

2). Учитывая координаты точки , из выражения вычислим значение параметра: =5. Значит кривая, содержащая точку , определяется функцией: . Вычислим производную этой функции: . Используя это выражение, вычислим направление касательной к кривой в точке : угловой коэффициент касательной в этой точке . Так как , то есть не совпадает с направлением поля, определяемым дифференциальным уравнением, то выражение не есть решение!

Ответ: не является.

☻

Задача-3. Моделируя некоторый процесс, специалист получил дифференциальное уравнение 1-го порядка, которое уже используется в практике других специалистов. Это значит, что известно общее решение этого уравнения, то есть известно множество интегральных кривых уравнения. Для специалиста важно, имея начальные условия процесса: , выделить интегральную кривую (частное решение), в соответствии с которой будет протекать процесс.

Решение:

1). Имея выражение общего решения: и заданные начальные условия: , запишем уравнение: . Решая уравнение относительно параметра , вычислим его значение , соответствующее заданным начальным условиям.

2). Заменяя в общем решении параметр значением , получим частное решение дифференциального уравнения: .

Ответ: получен общий алгоритм решения Задачи-3.

☺☺

Пример 1–09: В заданном семействе: выделить уравнение кривой, удовлетворяющей приведенному начальному условию: .

Решение:

1). Подставим в выражение значения: =0, =1. Тогда: , откуда находим значение параметра: =1, соответствующее заданным начальным условиям.

2). Заменяя в общем решении параметр значением =1, получим частное решение дифференциального уравнения: .

Ответ: кривая соответствует начальному условию .

Пример 1–10: В заданном семействе: выделить уравнение кривой, удовлетворяющей приведенному начальному условию: .

Решение:

1). Подставим в выражение значения: =0, =–1. Тогда: , откуда находим значение параметра: =–3, соответствующее заданным начальным условиям.

2). Заменяя в общем решении параметр значением =–3, получим частное решение дифференциального уравнения: .

Ответ: кривая соответствует начальному условию .

☻

Задача-4. Пусть задано семейство кривых: , где - параметр. Будем считать, что функция определяет неявную функцию (хотя при помощи этой же функции может быть определена неявная функция ). Необходимо составить дифференциальное уравнение, решением которого является это семейство.

Решение:

1). Используя функцию , запишем тождество:.Дифференцируя это тождество по переменной , получим:===0.

2). Запишем систему: Исключивпараметр из этой системы, получим дифференциальное уравнение, решением которого является семейство кривых: .

Ответ: получен общий алгоритм решения Задачи-4.

☺☺

Пример 1–11: Имеем семейство кривых: . Необходимо построить дифференциальное уравнение, для которого данное семейство кривых является решением.

Решение:

1). Считая, что выражение определяет неявнуюфункцию ,продифференцируем это выражение по независимой переменной . Имеем: .

2). Запишем систему: Для исключения из системыпараметра умножим первое уравнение на скобку, после чего приравняем левые части первого и второго равенств. Получено дифференциальное уравнение:, решением которогоявляется заданное семейство кривых.

Ответ: семейство кривых: является решением дифференциального уравнения: , или .

Пример 1–12: Имеем семейство гипербол: . Необходимо построить дифференциальное уравнение, для которого данное семейство кривых является решением.

Решение:

1). Считая, что выражение определяет неявнуюфункцию ,продифференцируем это выражение по независимой переменной . Имеем: . Умножив последнее на переменную , получим:.

2). Учитывая выражения: и , легко получаем (приравнивая правые части равенств) дифференциальное уравнение:, решением которогоявляется заданное семейство кривых.

Ответ: семейство кривых:является решением ДУ: .

☻

Замечание: Учитывая, обещанную в начале раздела, общность алгоритмов решения Задач для любых уравнений 1-го порядка, в представленных Примерах используемые дифференциальные уравнения не исследуются с целью определения их типа. Полученные алгоритмы будут использоваться для всех типов уравнений 1-го порядка по мере необходимости!..