Московский государственный институт электронной техники (Технический Университет).

А.Г.Фокин

Квантовая теория и статистическая физика

(Часть II)

Статистическая физика

Конспект лекций для студентов ЭКТ-2

2009г.

Оглавление

Оглавление 2

Решение задач по курсу “Статистическая физика” 44

Экзаменационные вопросы по курсу “Статистическая физика” 56

Экзаменационные задачи по курсу “Статистическая физика” 57

Дополнительные задачи по курсу “Статистическая физика” 59

§1. Статистическое описание систем с большим числом степеней свободы

Статистическая физика изучает системы с большим числом степеней свободы. Наличие большого число степеней свободы вносит некоторые особенности в описание таких систем. Например, в воздуха содержитсячастиц (число Лошмидта), но у каждой материальной точки (частицы) имеется 3 степени свободы, поэтому у этой системы огромное число степеней свободы.

В классической механике возможно описывать такие системы (через формализм Гамильтона) - динамических переменных, где- число степеней свободы. Описание системы сводится к решению уравнений:

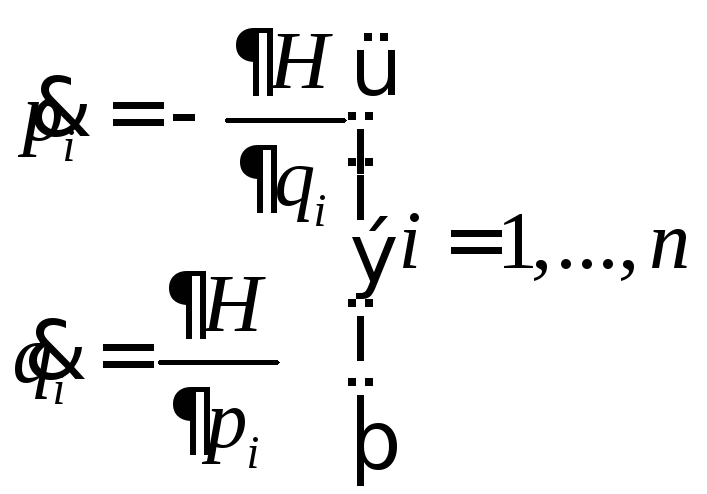
Чтобы решить данную систему, необходимо задать начальных условий. Задаем начальные условия и решаем систему. Но здесь сложные технические трудности(долгий счёт на ЭВМ). Но имеются ещё и качественные особенности этих систем, которые не охватываются этими уравнениями, т.е. детерминированный подход здесь не используют.

Статистическая физика рассматривает переход от малого числа степеней свободы к большому. и- это динамические переменные. Фазовое пространство – этомерное пространство, декартовыми осями которого являются переменныеи. Тогда состояние системы (которое задаётся динамическими переменными) в фазовом пространстве задаётся фазовой точкой. Движение системы в реальном пространстве задаётся движением фазовой точки в фазовом пространстве, т.е. устанавливается соответствие между фазовым и реальным пространствами.

§2. Метод статистической физики(элементы теории вероятностей)

Основной метод статистической физики – теория вероятностей. В теории вероятностей для описания событий задаётся, или вводится, вероятность:

-поле событий,- вероятность, тогда:

При изучении конкретных систем, для измерения вероятностей используется закон больших чисел, который разработал Чебышёв. На основе закона больших чисел вводится аксиома измерений вероятностей (в абстрактной теории закона измерения нет), через частоту появления события и через предельные соотношения.

Далее, в теории вероятностей вводится либо дискретное, либо непрерывное множество.

На ряду с вводится:

- вероятность того, что некоторая величина заключена в интервале:

Здесь - плотность вероятности. Плотность вероятности вводится для непрерывных объектов, случайных процессов и полей, которые сплошь заполняют исследуемые множества.

Под понимаетсяв момент времени:

Запишем -точечную функцию распределения(или плотность распределения):

Здесь ,.

Функции обладают определённым набором свойств:

1. Неотрицательность

2. Симметричность, т.е. инвариантность относительно перестановок:

3. Согласованность, т.е. после интегрирования 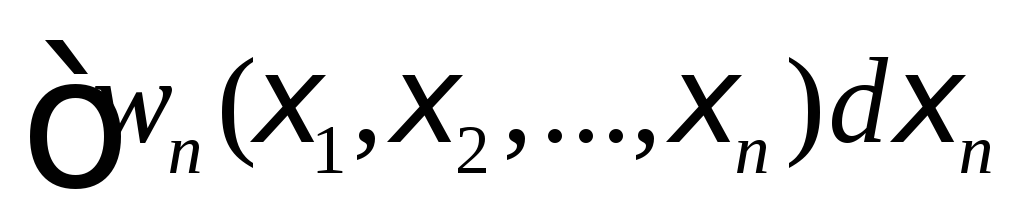получаем:

4. Нормированность на единицу: