малой, чтобы можно было считать, что в пределах S вектор Е const ,

где – локальная поверхностная плотность заряда, разная в разных точках поверхности.

Поверхностную плотность заряда шара можно выразить не через заряд

пропорциональна радиусу шара R . Этот результат имеет общий характер. Какой бы сложной формой ни обладал проводник, потенциал во всех его точках одинаков, т. е. const . Поэтому поверхностная плотность заряда

будет больше в тех местах, где меньше радиус кривизны, т. е. где поверхность искривлена сильнее. Очевидно, что в этих же местах будет больше в соответствии с (3.89) и напряженность электрического поля.

3.8 Электроемкость уединенного проводника. Конденсаторы.

Уединенным проводником называется проводник, настолько удаленный от других проводников, тел и зарядов, что их влиянием на рассматриваемый проводник можно пренебречь. Опыт показывает, что разные уединенные проводники, будучи заряженными одинаковыми

30

зарядами, принимают различные потенциалы. Однако для каждого проводника между зарядом q и его потенциалом существует прямая

называют электроемкостью или просто емкостью уединенного проводника. Из (3.91) ясно, что она численно равна заряду, сообщение которого проводнику изменяет его потенциал на единицу. Емкость уединенного проводника зависит от его размеров и формы. Например, для заряженного проводящего шара радиуса R его потенциал равен

Как следует из (3.93) для того, чтобы проводник обладал большой емкостью, его размеры должны быть огромными. На практике же необходимы устройства, обладающие способностью накапливать значительные заряды при малых размерах и малых потенциалах. Это удалось осуществить в связи с тем, что если к заряженному проводнику приближать другие тела, то его емкость может существенно увеличиваться. Приближение этих тел к проводнику приводит к тому, что электрическое поле проводника вызывает появление на приближающихся проводниках индуцированных зарядов, причем ближайшими к заряду проводника q будут индуцированные

им заряды противоположного знака, что приводит к уменьшению потенциала проводника, являющегося алгебраической суммой потенциала собственных зарядов проводника и зарядов, индуцированных на других телах. Поскольку заряд q самого проводника при этом не изменяется, то в соответствии с

(3.91) его емкость увеличивается. Это позволило создать систему проводников, которая обладает емкостью гораздо большей, чем уединенный проводник. Такая система называется конденсатором, который, как правило, состоит из двух проводников (обкладок конденсатора), разделенных малым пространственным промежутком, заполненным диэлектриком. На емкость конденсатора не должны оказывать влияния окружающие его тела, поэтому обкладкам придают такую форму, чтобы поле, создаваемое накопленными на них зарядами, было сосредоточено в узком зазоре между обкладками. Тогда оно не будет индуцировать заряды на окружающих конденсатор телах. Этому условию удовлетворяют две плоские пластины (плоский конденсатор), два коаксиальных цилиндра (цилиндрический конденсатор), две

31

концентрические сферы (сферический конденсатор). Поскольку поле должно

быть сосредоточено между обкладками, то линии вектора Е , начинающиеся на одной обкладке, должны заканчиваться на другой, т. е. заряды на обкладках должны быть равны по модулю и противоположны по знаку ( q

и - q ). В связи с этим между обкладками существует разность потенциалов или напряжение U и под электроемкостью конденсатора понимают отношение модуля заряда пластин, к напряжению на его обкладках

Емкость конденсатора зависит от его геометрии, т. е. от размеров и формы обкладок, от зазора между ними и от заполняющего этот зазор диэлектрика.

Рассчитаем, например, емкость плоского конденсатора, состоящего из двух металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга. Если расстояние d гораздо меньше линейных

Если пространство между пластинами заполнено диэлектриком с диэлектрической проницаемостью , то напряженность поля Е и вместе с ней разность потенциалов уменьшится в раз, а емкость во столько же раз возрастет :

Для увеличения емкости, а так же для возможности варьирования еѐ величины в широких пределах конденсаторы соединяют в батареи, используя их параллельное и последовательное включение.

32

Таким образом, при последовательном соединении конденсаторов, суммируются величины, обратные их емкостям. И емкость такой батареи С всегда меньше наименьшей емкости Ci , используемой в батарее.

3.9 Энергия системы неподвижных зарядов. Энергия заряженного проводника и конденсатора. Энергия и объемная плотность энергии электрического поля. Энергия поляризованного диэлектрика.

Ранее было установлено, что электростатические силы консервативны. Это означает, что система зарядов обладает потенциальной энергией

33

…qi, …, qn можно установить, что энергия взаимодействия системы из n неподвижных точечных зарядов равна:

Рассмотрим уединенный заряженный проводник, заряд которого q, потенциал – , а емкость – С. Увеличим заряд этого проводника на элементарно малую величину dq, настолько малую, что потенциал

практически не изменится. Для этого необходимо этот заряд dq перенести из бесконечности на проводник. Затраченная на этот перенос работа

Для того чтобы зарядить проводник от нулевого потенциала до потенциала, необходимо совершить работу

Повторяя такую же процедуру для конденсатора, т.е. перенося заряд dq с одной обкладки на другую и совершая при этом элементарную работу

34

dA Udq UCdU найдем работу по зарядке конденсатора до разности потенциалов U, а, следовательно, и энергию заряженного конденсатора

где V Sd – объем конденсатора с напряженностью поля в конденсаторе Е. Это, по-видимому, означает, что носителем энергии является электростатическое поле. Поскольку поле плоского конденсатора однородно,

то из (3.109) следует, что плотность энергии или энергия, сосредоточенная в единице объема поля равна

справедливой для любых электростатических полей, если в ней под Е и D понимать значения этих величин в каждой рассматриваемой точке. В этом случае, зная плотность энергии в каждой точке можно найти энергию W поля в любом объеме V, проведя интегрирование по этому объему:

35

диэлектрика, то выражение (3.113) содержит кроме плотности энергии поля

3.10 Постоянный электрический ток и его характеристики и условия существования. Обобщенный закон Ома.

Закон Джоуля – Ленца. Правила Кирхгофа.

Электрическим током называется упорядоченное, т. е. направленное движение электрических зарядов. Ток проводимости в проводящем ток веществе осуществляется свободными зарядами, называемыми носителями тока – электронами в металлах, электронами и дырками в полупроводниках, ионами в электролитах, электронами и ионами в плазме.

Направлением тока условно принято считать направление движения положительных зарядов. Поэтому направление тока, например, в металлах противоположно истинному направлению движения носителей тока в них – электронов.

Для существования электрического тока необходимо наличие в веществе свободных носителей зарядов и электрического поля, которое вызывало бы их направленное движение. В отличие от электростатики, где рассматривается равновесие зарядов и поэтому электрическое поле в

проводниках отсутствует, для существования тока напряженность

электрического поля E внутри проводника должна быть отлична от нуля.

Для создания и поддержания тока необходимо не только создать внутри

проводника поле E , но и непрерывно поддерживать его постоянным, так чтобы энергия этого поля затрачивалась на работу по перемещению зарядов. Для этого энергия поля должна все время пополняться и, следовательно,

необходимо такое устройство, в котором какой-либо вид энергии преобразовывался в энергию электрического поля. Такое устройство называется источником электродвижущей силы, или источником тока.

Для количественной характеристики электрического тока вводятся две основные величины – сила тока I и плотность тока j . Силой тока I

называется скалярная физическая величина, численно равная заряду, переносимому через поперечное сечение проводника за единицу времени:

36

где dq – электрический заряд, проходящий через поперечное сечение

проводника за бесконечно малое время dt. Если сила тока и его направление не изменяются с течением времени, то ток называется постоянным и сила

постоянного тока равна:

где q – электрический заряд, прошедший через поперечное сечение проводника за произвольно выбранный промежуток времени t . Единица силы тока в системе единиц СИ Ампер (A) является основной и ее определение будет дано позже.

Для характеристики распределения тока по перечному сечению проводника вводится вектор плотности тока j . Этот вектор направлен вдоль тока и его модуль численно равен силе тока dI через расположенную в данной точке перпендикулярную к направлению тока площадку величине этой площадки.

j dI . dS

Очевидно, что плотность тока j определяется зарядом, проходящим через единичную площадку, перпендикулярную направлению движения зарядов в

единицу времени. С микроскопической точки зрения ток, протекающий через сечение dS (рис. 3.26) за время dt – это заряд, содержащийся в цилиндре

однородного проводника можно создать, приложив к концам этого участка напряжение (разность потенциалов) U и поддерживая его постоянным. В 1826 г. Г. Ом экспериментально установил, что сила тока I , текущего в таком участке проводника пропорциональна приложенному напряжению.

37

где R – электрическое сопротивление проводника. Уравнение (3.120) выражает закон Ома для однородного участка цепи. Сопротивление проводников зависит от их размеров и формы, а также от материала, из которого изготовлен проводник. Для однородного линейного проводника

длиною l с неизменным поперечным сечением S сопротивление R равно:

где – коэффициент пропорциональности, характеризующий материал

проводника и называемый удельным сопротивлением. Опыт показывает, что удельное сопротивление металлов линейно зависит от температуры в довольно широком интервале ее изменения:

где t – температура металла по шкале Цельсия, 0 – удельное сопротивление

при 0ºC, а – температурный коэффициент сопротивления, который для чистых металлов при не очень низких температурах имеет численное значение, близкое к 1/273 на градус температуры. Вводя термодинамическую температуру (шкала Кельвина), температурную зависимость сопротивления можно записать в виде:

где R0 – сопротивление однородного участка при t = 0ºC.

Закон Ома можно представить в так называемой дифференциальной форме, подставив в (3.120) выражение (3.121) и учтя, что в однородном

38

Выражение (3.126) и называется законом Ома в дифференциальной форме. Оно связывает плотность тока в любой точке внутри проводника с напряженностью поля в этой же точке. Оно оказывается справедливым и для переменных полей.

За время dt через поперечное сечение проводника переносится заряд dq Idt . При этом электрическое поле совершает работу

Очевидно, что при прохождении тока в неподвижном проводнике из-за наличия сопротивления вся работа поля идет на нагревание проводника, т.е. dA dQ и следовательно

Выражение (3.130) представляет собой так называемый закон ДжоуляЛенца, экспериментально установленный независимо друг от друга Дж. Джоулем и Э. Ленцем.

Выделим в проводнике элементарный цилиндрический объем dV dS dl так, чтобы ось цилиндра совпадала с направлением тока. По

закону Джоуля-Ленца за время dt в этом объеме выделится количество теплоты

выделяющейся в единице объема проводника за единицу времени. Тогда

39

Формула (3.132) выражает закон Джоуля-Ленца в т. н. дифференциальной форме.

Если в проводнике создать электрическое поле и не принять мер для его поддержания, т. е. для поддержания разности потенциалов, то перемещение, например, положительных зарядов от конца проводника с большим потенциалом к концу с меньшим потенциалом достаточно быстро приведет к выравниванию потенциалов, поле внутри проводника исчезнет и ток прекратится. Для поддержания постоянного тока необходимо от конца проводника с меньшим потенциалом непрерывно отводить приносимые сюда током положительные заряды и подводить их к концу большим потенциалом. Такое перемещение можно осуществлять только с помощью сил неэлектростатического характера. Такие силы называют сторонними силами. Сторонние силы можно охарактеризовать работой, которую они

совершают над перемещающимися зарядами Aст. Величина, численно равная работе сторонних сил над единичным положительным зарядом, называется E , действующей в цепи или на ее участке,

где векторную величину Eст называют напряженностью поля сторонних

сил. Работу сторонних сил производит в цепи источник тока. Участок цепи, содержащий источник тока, называют неоднородным участком. На таком

Работа, совершаемая этой силой равна:

Величина, численно равная работе, совершаемой электростатическими и сторонними силами при перемещении единичного положительного заряда,

40

где R12 R r представляет собой сумму внутреннего сопротивления

источника r, и сумму внешних сопротивлений R участка цепи 1-2. Его называют внешним сопротивлением участка цепи. Это уравнение выражает интегральную форму закона Ома для неоднородного участка цепи.

Из (3.138) следует, что если цепь замкнута, т.е. 1 2 , то выражение приобретает вид:

Это уравнение называется законом Ома для замкнутой цепи. В нем R представляет собой полное внешнее сопротивление замкнутой цепи. Запишем закон Ома для замкнутой цепи в виде

где UR — напряжение на общем внешнем сопротивлении R, а Ur —

Часть этой мощности, соответствующая тепловым потерям на внутреннем сопротивлении, равна I2r и полезная мощность P0 , передаваемая источником во внешнюю цепь, равна:

41

Отношение полезной мощности P0 , к полной мощности Р называется

коэффициентом полезного действия источника тока.

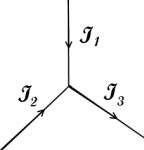
На практике часто приходится рассчитывать токи и падения напряжений на участках сложных разветвлѐнных цепей, в разных ветвях которых находятся источники тока и различные внешние сопротивления. Расчѐт таких цепей производится с помощью т. н. правил Кирхгофа. Первое правило относится к так называемым узлам цепи. Узлом называется точка в которой сходится более чем два проводника (рис. 3.27). Ток, текущий к узлу, можно считать положительным, а текущий от узла — отрицательным.

i 1

Второе правило Кирхгофа является обобщением закона Ома и состоит в следующем: в любом замкнутом контуре разветвлѐнной цепи алгебраическая сумма произведений токов Ii на сопротивление Ri соответствующих участков этого контура равна алгебраической сумме ЭДС Ei в выбранном контуре

Для составления уравнения (3.146) необходимо выбрать направление обхода контура, например, по ходу часовой стрелки, произвольно выбрать направления токов во всех участках контура, следя за вышеприведѐнным правилом для узлов. Все токи в (3.146), совпадающие по направлению с выбранным направлением обхода контура, считаются положительными, а

несовпадающие – отрицательными. ЭДС Ei источников тока в контуре

считаются положительными, если они создают ток, направленный в сторону направления обхода, (т. е. если в направлении обхода источник проходится от – к + ) и отрицательным, если создаваемый ими ток противоположен направлению обхода (от + к – ).

42