Министерство образования и науки Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

«Санкт-Петербургский государственный технологический институт (технический университет)»

Кафедра общей физики

Н. Г. Москвин

Глава 3. Электростатика. Основные законы постоянного тока.

Конспект лекций по физике

под редакцией д.т.н., профессора Кашмета В. В.

Издательство СПбГТИ(ТУ)

Санкт-Петербург

2011

3.ЭЛЕКТРОСТАТИКА. ОСНОВНЫЕ ЗАКОНЫ ПОСТОЯННОГО ТОКА.

3.1.Электростатика. Электрический заряд. Электростатическое поле. Вектор напряженности электрического поля, силовые линии.

Вокружающем нас макромире всѐ многообразие встречающихся сил, кроме сил тяготения, представляет собой проявление электромагнитных взаимодействий. При изучении законов механики мы встречались с силами упругости и с силами трения. Несмотря на внешние различия этих сил, они имеют общую физическую природу – это электромагнитные силы.

Благодаря электромагнитному взаимодействию мы можем видеть окружающий мир, так как свет представляет собой электромагнитную волну. Электромагнитное взаимодействие характеризуется наибольшей широтой и разнообразием проявлений в природе. Так происходит потому, что все вещества состоят из электрически заряженных частиц (протонов и электронов), электромагнитное взаимодействие между которыми во много раз интенсивнее гравитационного взаимодействия.

Электромагнитным взаимодействием определяется строение и свойства вещества – атомов, молекул, жидкостей, твердых и газообразных состояний вещества. Взаимодействие заряженных частиц друг с другом осуществляется посредством электромагнитного поля. Оно представляет собой совокупность двух взаимосвязанных полей – электрического и магнитного.

Источниками электрического поля служат любые электрические заряды, магнитное поле создается движущимися зарядами. Соотношение между электрическим и магнитным полями меняется при переходе из одной инерциальной системы в другую.

Изучение электромагнитных взаимодействий, которым занимается электродинамика, начнѐм с простейшего случая – с электростатики, в которой рассматривается взаимодействие неподвижных в инерциальной системе отсчета зарядов и создаваемое ими неизменное во времени электрическое поле, называемое электростатическим.

Электрический заряд и электростатическое поле – первичные понятия, подобно понятиям массы и гравитационного поля.

Электрический заряд – физическая величина, определяющая интенсивность электромагнитного взаимодействия. Существуют два рода электрических зарядов, условно названных положительными и отрицательными. Заряды одного знака отталкиваются, заряды противоположных знаков притягиваются. Носителями отрицательного заряда в веществе являются электроны, положительного – протоны.

Заряд протона е равен минимальному встречающемуся в природе заряду, называемому поэтому элементарным электрическим зарядом:

2

Заряд электронов – отрицательный и по абсолютной величине равен элементарному электрическому заряду (3.1).

Атом любого элемента содержит столько же электронов в электронной оболочке, сколько протонов находится в его ядре. Поэтому атом электрически нейтрален. По этой причине нейтральными являются молекулы и все макроскопические тела.

Однако любому телу можно сообщить тем или иным способом избыточный заряд. Это произойдет в том случае если число электронов Nе и число протонов Nр в теле станут разными. В этом случае заряд тела q

Если заряд тела q во много раз превышает величину элементарногоq e , то удобно отвлечься от дискретности заряда и представить его непрерывно распределенным по объему, поверхности или линии. При этом вводят понятие о плотности зарядов – объемной , поверхностной σ и

Электрический заряд обладает свойством инвариантности: его величина не изменяется при переходе из одной инерциальной системы к другой.

Важнейшее свойство электрического заряда выражается законом сохранения заряда: в изолированной системе алгебраическая сумма зарядов при любых происходящих в ней процессах не изменяется. Это один из фундаментальных законов природы.

Согласно современным представлениям взаимодействие между зарядами осуществляется через поле. Всякий покоящийся в выбранной

инерциальной системе отсчета электрический заряд q изменяет определенным образом свойства окружающего его пространства – создаѐт в нем электростатическое поле. Это поле проявляет себя в том, что помещенный в какую-либо его точку другой заряд испытывает действие силы со стороны поля. Назовем этот другой заряд пробным. Условимся считать этот пробный заряд точечным. Понятие точечного заряда аналогично понятию материальной точки в механике. Точечным зарядом назовем

3

заряженное тело, размерами которого можно пренебречь в условиях рассматриваемой задачи. Практически это будет какое-то заряженное тело, имеющее настолько малые размеры, чтобы можно было судить о свойствах поля в определенной точке пространства (заряженная материальная точка). В действительности этот точечный заряд может представлять собой совокупность большого числа элементарных зарядов. С другой стороны

пробный электрический заряд (qпр) должен быть достаточно малым, чтобы можно было пренебречь влиянием этого заряда на распределение зарядов, создающих изучаемое поле. Другими словами, пробный заряд не должен своим присутствием искажать электростатическое поле, которое с его

не зависит от величины пробного заряда. Следовательно, это отношение

можно использовать для силовой характеристики электростатического поля.

Вектор E , введенный таким образом, называют вектором напряженности электрического поля. Его, как видно из (3.5), можно определить как силу, рассчитанную на единицу пробного заряда. Знание напряженности электрического поля позволяет найти силу, действующую на

Как же найти напряженность электрического поля в какой-либо точке? Рассчитать напряженность электростатического поля точечного заряда можно с помощью закона Кулона. В результате проведенных опытов Кулон в

1785 г. установил, что сила взаимодействия двух точечных зарядов q1 и q2 в вакууме (воздухе) пропорциональна произведению величин этих зарядов и обратно пропорциональна квадрату расстояния между ними.

4

сферически симметричным распределением заряда (шар и сфера с равномерным распределением заряда по поверхности сферы или по объему шара) описывается таким же выражением (3.7), где r – расстояние между их геометрическими центрами и, что этот закон очень похож на закон всемирного тяготения, только роль масс здесь играют заряды.

Будем считать некоторый точечный заряд q источником электростатического поля. Это поле действует на расположенный на

него и, следовательно, действительно может служить векторной (силовой) характеристикой поля.

Формула (3.11) представляет собой не что иное, как закон Кулона в так называемой полевой форме. Отметим, что в поле, создаваемом неподвижным точечным зарядом, сила, действующая на пробный заряд, не

электрического поля. Эти линии проводят так, чтобы в каждой еѐ точке

вектор E был направлен по касательной к силовой линии. Кроме того, этим

5

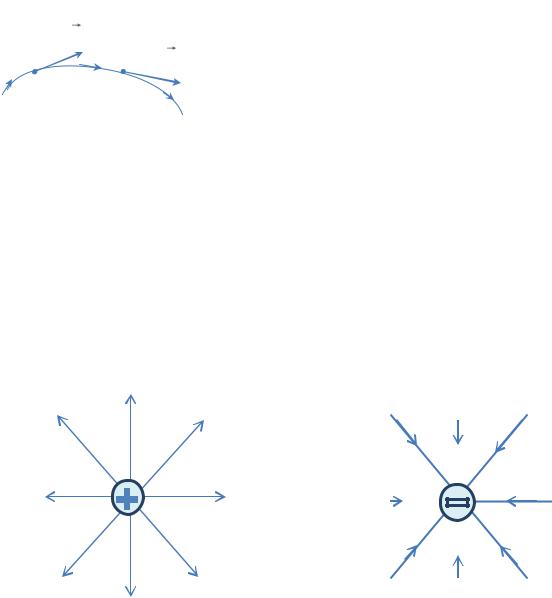
точечного уединѐнного заряда они приходят из бесконечности и заканчиваются на заряде. Поскольку уединѐнный заряд является абстракцией, то можно сказать, что силовые линии начинаются на положительных зарядах и оканчиваются на отрицательных. Вообще направление силовой линии в каждой точке поля, как это следует из (3.5), совпадает с направлением силы, действующей на пробный (положительный!)

заряд, помещенный в эту точку. Очевидно, что силовые линии не могут

пересекаться, ибо в противном случае вектор E не имел бы в точке пересечения определенного направления.

Из рис. 3.1 и 3.2 видно, что линии проведены гуще там, где напряженность поля больше (см. 3.10), и реже там, где она меньше. Это означает, что число

силовых линий, пронизывающих единичную площадку, перпендикулярную

силовой линии в данной точке, пропорционально модулю вектора E . По картине силовых линий легко, таким образом, судить о конфигурации

рассматриваемого электрического поля, т. е. о направлении модуля вектора

Eв разных точках поля.

3.2Принцип суперпозиции. Поток вектора напряженности.

Теорема Гаусса, и её применение.

6

Основной задачей электростатики является нахождение в каждой точке

поля величины и направления вектора напряженности E по заданному распределению в пространстве зарядов.

Пусть поле создано системой неподвижных точечных зарядов q1, q2, ...,

qi,…, qn. Из рассмотренного в механике принципа независимости действия сил следует, что сила взаимодействия двух данных зарядов не изменится,

т.е. напряженность электрического поля, создаваемая системой точечных зарядов, равна векторной сумме напряженностей полей, создаваемых каждым из этих зарядов. Полученный результат называется принципом суперпозиции (наложения) полей.

Всякое заряженное тело можно разбить на столь малые части (материальные точки), что каждую из них можно считать точечным зарядом. Поэтому формула (3.13) принципиально пригодна для расчетов любых электрических полей.

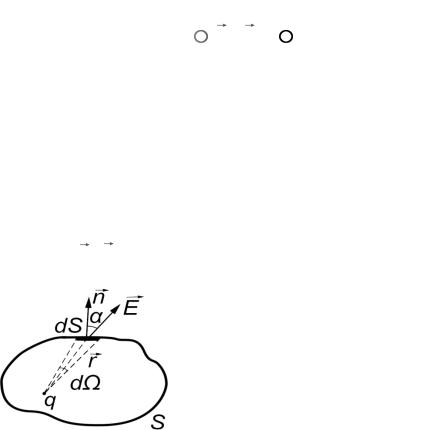
Теперь воспользуемся геометрической картиной описания электрического поля, причем будем считать, что число силовых линий,

7

dS – вектор, модуль которого равен dS , а направление совпадает с

нормалью n к площадке.

Вычисленный по формуле (3.15) поток – величина алгебраическая и зависит не только от конфигурации поля, но и от выбора направления нормали. Договорились для замкнутых поверхностей нормаль n направлять наружу области, охватываемой этой поверхностью, т.е. выбирать внешнюю

нормаль (не направленную внутрь охватываемой области).

Понятие потока вектора напряженности E является очень важным в связи с тем, что существует теорема Гаусса, в соответствии с которой

поток вектора E сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов qi, охватываемых этой поверхностью,

где значок у интеграла означает, что он берѐтся по всей замкнутой поверхности.

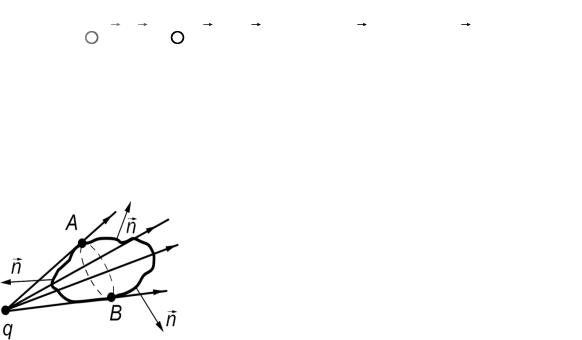
Для доказательства этой теоремы сначала рассмотрим поле одного

8

В алгебраическую сумму войдут только те заряды, которые находятся внутри области, охватываемой замкнутой поверхностью S. Это следует из

Теорема Гаусса позволяет в ряде случаев найти напряженность поля гораздо проще, чем с использованием принципа суперпозиции по формуле (3.13) . Однако, использование этой теоремы эффективно лишь в тех случаях, когда поле обладает некоторой симметрией – плоской, сферической или цилиндрической. Оказывается, что в этих случаях конфигурация поля такова, что легко найти достаточно простую по форме замкнутую поверхность, так

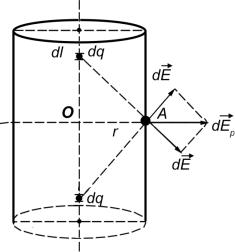
что интегрирование в формуле (3.19) сводится к простому умножению Еn на площадь поверхности S или какую-либо еѐ часть. В качестве примера рассмотрим задачу о нахождении напряженности поля Е, создаваемого

бесконечной равномерно заряженной нитью (цилиндром) на расстоянии r от неѐ (рис. 3.6) .

9

Так как нить бесконечно длинная, то всегда можно найти на ней такой же

стороны, выбранная поверхность охватывает участок нити длиной h, заряд которой q h. Следовательно

Используя теорему Гаусса легко найти напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью с поверхностной

плотностью заряда . Из симметрии задачи, проведя рассуждения,

E

10

площадь S и расположены симметрично относительно заряженной плоскости (рис. 3.7). Поток сквозь боковую поверхность этого цилиндра равен нулю, а

Пусть имеются две параллельные бесконечные плоскости, заряженные равномерно разноименными зарядами с поверхностными плотностями зарядаи . Поле, создаваемое этими плоскостями, можно найти как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. На

рис. 3.8 верхние стрелки соответствуют полю от положительно заряженной плоскости, а нижние – от отрицательной плоскости.

По принципу суперпозиции результирующая напряженность поля между плоскостями

по принципу суперпозиции равно нулю. Таким образом, всѐ поле сосредоточено между плоскостями и является, как и поле одной пластины, однородным.

Полученный результат приближенно справедлив и для пластин конечных размеров, если расстояние между пластинами значительно меньше их линейных размеров. Отметим также, что формулу (3.22) можно применять и для нитей (цилиндров) конечных размеров на расстояниях от них значительно меньших линейных размеров нити (цилиндра).

Наконец, покажем, что формула для напряженности поля точечного заряда справедлива и для равномерно заряженных сферы или шара радиусом

11