9.1) Основные типы нелинейностей.

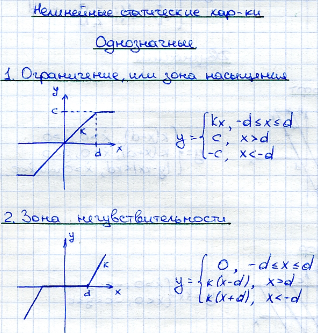
3.Комбинация ограничения и зоны нечувст.

9.2)

10.1) Понятие фазовой плоскости, фазовой траектории и фазового портрета.

Дифференциальное уравнение системы автоматического управления может быть преобразовано в систему n дифференциальных уравнений 1-го порядка

(7.1)

с начальными условиями x_i(0). Величины x_i(t) можно рассматривать как координаты некоторой точки М, называемой изображающей точкой, в n – мерном пространстве. Изображающая точка при изменении координат описывает в этом пространстве некоторую кривую, которая называется фазовой траекторией. Совокупность фазовых траекторий, полученных при различных начальных условиях, называется фазовым портретом системы. Наглядное представление фазовых траектория возможно только для систем, порядок которых не выше второго, или для систем, которые могут быть сведены к системам второго порядка. Исследование поведения нелинейных систем, ниже излагаемым методом, возможно только для автономных стационарных систем. Система является автономной, если ее правая часть явно не зависит от времени.

Уравнение автономной системы 2-го порядка можно записать в виде

(7.2) Полагая получим

(7.3)

10.2) Фазовыми координатами являются выходная переменная системы x₁ и скорость ее изменения x₂. Разделим второе уравнение системы на первое и получим дифференциальное уравнение фазовых траекторий

(7.4)

Уравнение (7.4) однозначно определяет касательную к фазовой траектории во всех точках, кроме тех, в которых одновременно выполняются равенства

(7.5)

В этих точках, которые называются особыми точками, не существует определенного направления касательной к траектории. В особых точках фазовые координаты равны нулю, следовательно, в этих точках система находится в положении равновесия.

Метод фазовой плоскости для исследования нелинейных систем.

В качестве первой координаты мы выбираем(условно) перемещение, в качестве второй – скорость изменения перемещения. 1я координата – по горизонтали, по вертикали – скорость.

Из-за этого договора следует, что фазовые траектории четко направлены. Изменяющийся параметр – время. Если скорость больше нуля, то перемещение может только возрастать, если меньше нуля, то только убывать. Хоть метод гармонического баланса является

10.3) приближенным, но он применим к системам любого порядка, когда как метод исследования на «фазовой плоскости» (точный) применим только к системам второго порядка. Наши нелинейности будут кусочнолинейными, то есть для каждого отрезка прямой линии статическ. хар-ки мы получаем семейство линейных решений. На границе придется сопрягать линейные семейства(нелинейность).

Каждая точка фазовой плоскости отражает одно состояние системы и называется фазовой, изображающей или представляющей точкой.Изменение состояния системы отображается на фазовой плоскости движением этой точки. След от движения изображающей точки называется фазовой траекторией. Через каждую точку фазовой плоскости проходит лишь одна фазовая траектория, за исключением особых точек. Стрелками на фазовых траекториях показывается перемещение изображающей точки с течением времени. Полная совокупность различных фазовых траекторий — это фазовый портрет. Он даёт представление о совокупности всех возможных сочетаний системы и типах возможных движений в ней.

11.1).=;;=>

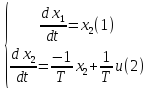Нужно исключить из этих ур-йtчтобы получить фазовой пл-ти траекторию

1. 

1. u=+c;; разделяем переменные :

проинт.последнее выражение:

;

←неуст.полож.равновесия.

2.u=-c; →

11.2)

3.u=0; →

Рис:

12)

13) Метод изоклин

Нелин. урав. Задает траекторию, называемую изоклином – траектория вдоль которой будет const производная фаз. траектории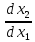

14)

15)

16)

17.1) Метод гармонического баланса

сигналыg(t) и выход сист. знач. не имеют.g(t)=0

Безинерц-ая нелин-ть(которая симметрична относ. начала координат)отделена от динамич лин-й части.

Предположим, что в этой системе найдется переодич-ое решение: будем считать, что на входе линейного элемента сигнал x(t), на выходеy(t). Сигналg(t) и выход значения не имеют.

тогда на выходе:

Пользуемся методом гармон-й линеаризации нелин-ти. Сигнал на выходе y(t) мы заменяем 1-й гармоникой:

Передаточная функция линейной части д.б. фильтром низких частот. Вводится погрешность

Идет линеаризация:

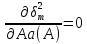
17.2)

Аналогично получаем:

- перешли к другой переменной

Преобразование сигнала, проходящего через нелин. Элемент.

17.3)

Для однозначной нелинейности:

Для 2-хзначной нелинейности:

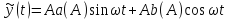
Вывод: становится важно, растет или убывает сигнал.

В результате гармонической линеаризации не теряем свойства, присущее линейным элементам.

Коэффициент гармонической линеаризации не зависит от частоты(при нашей постановке задачи)

Введем понятие эквивалентного гармонически линеаризованного коэффициента усиления

Фаза сдвигается, кода есть косинусная составляющая b(A)