1 Единичное состояние о.С.

5 Единичное состояние о.С.

Горизонтальное перемещение т. В, вызванное действием сил , равно нулю.

По теореме Максвелла о взаимности перемещений: 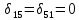, т.е. взаимное перемещение по вертикали сечений С₁ и С₂, вызванное действием силы , равно нулю.

Чтобы определить перемещение ∆_3F, необходимо построить и перемножить эпюры от сил и.

1 1

1 1 P

D

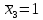
3 Единичное состояние о.С.

Грузовое состояние О.С.

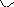
1 1

Решая систему канонических уравнений, находят лишние неизвестные x_i. Окончательную эпюру изгибающих моментов строят, используя принцип суперпозиции.

Для проверки правильности эпюры М используют статическую и кинематическую проверки. Статическая заключается в проверке равновесия всех узлов рамы, выделенных из конструкции и находящихся под действием изгибающих моментов в сходящихся стержнях и внешних моментов, приложенных в узлах. Например, для эпюры M_F получаем для узла D:

0

D - узелD в равновесии.

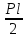
Кинематическая проверка заключается в отсутствии суммарных перемещений в заданной системе по направлению отбрасываемых связей:

т.е. необходимо перемножить каждую из единичных эпюр 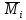на окончательную эпюруМ. Если ноль не получается, то допущена как минимум одна ошибка в расчетах (при первом расчете таких ошибок несколько). Для того, чтобы избежать неопределенности в нахождении ошибки, разработана система пошаговых промежуточных проверок.

Эпюра поперечных сил Q для простых рам строится методом сечений. Для сходных рам эпюру Q строят путем вырезания отдельных стержней рамы с последующим рассмотрением их равновесия под действием внешних нагрузок и внутренних усилий по концам стержней. Так как нагрузки известны, изгибающие моменты можно принять с окончательной эпюры М, а продольные силы в составлении уравнений равновесия не участвуют, то можно вычислить поперечные силы по концам стержней.

Рассмотрим стержень ij:

y P q M

M_ij i j M_ij

N_ij

N_ij

Q_ij Q_ij

a

b

l

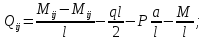
Эпюру продольных сил N для простой рамы можно построить методом сечений. Для схожей рамы эпюру N строят путем рассмотрения равновесия вырезанных узлов, находящихся под действием активных нагрузок поперечных сил, взятых с эпюры Q, и продольных сил. Необходимо последовательно рассматривать узлы, в которых неизвестными являются не более двух продольных сил. Например, для узла k получаем:

P₁ N_kj j

P₂ K Q_kj

Q_ki

N_ki

i

Для статической проверки всей рамы в целом необходимо приложить все опорные реакции и составить три уравнения равновесия, которые должны тождественно выполняться ():

Метод перемещений

Рассмотрим альтернативный по отношению к методу сил метод раскрытия статической неопределимости стержневых систем, названный методом перемещений. В методе сил за неизвестные принимают реакции и (или) внутренние усилия в лишних связях, которые находят из равенства нулю перемещений по направлению отброшенных связей. В методе перемещений за неизвестные принимают перемещения подвижных узлов конструкции, которые находят из равенства нулю реакций в воображаемых опорных связях, препятствующих перемещениям узлов: в методе сил часть связей отбрасывается, а в методе перемещений, наоборот, вводится некоторое число новых связей. На первый взгляд, кажется, что мы усложняем задачу, вводя дополнительные связи, но благодаря оригинальному подходу это не так. Дело в том, что вводя в реальную конструкцию ряд виртуальных связей, мы получаем набор базовых случаев нагружения балок, используемых при расчете большого многообразия стержневых систем. Такой подход легко поддается программированию на ЭМВ.

Рассмотрим простую П-образную раму и представим возможную схему ее деформации при воздействии внешних нагрузок с учетом следующих упрощающих предпосылок:

1. Стержни при изгибе искривляются, но своей длины не изменяют;

2. Жесткие узлы поворачиваются так, что углы между примыкающими стержнями не изменяются.

Жесткие узлы D, E, F, G повернутся на некоторые углы θ₁-θ₄ и переместятся по горизонтали на величину ∆₁ и ∆₂. Т.к. стержни не растяжимы, то DD₁=EE₁=∆₁ и FF₁=GG₁=∆_2. Таким образом общее число неизвестных равно степени кинематической неопределимости n_k=n_y+n_л=4+2=6.

Число угловых неизвестных n_y равно числу жестких узлов рамы. Число линейных неизвестных n_л равно числу степеней свободы шарнирной модели. n_л=W_ш.м.=3D-2U_ш-С=3*6-2*8-0=2.

Выбираем основную систему метода перемещений, вводя в жестких узлах виртуальные (воображаемые) заделки, препятствующие повороту, и линейные связи в узлах E, G, препятствующие горизонтальному перемещению.

Если теперь повернуть виртуальные заделки на углы θ₁-θ₄ и сместить линейные связи на величину ∆₁ и ∆₂, и кроме того приложить внешние нагрузки , то мы получимэквивалентную систему, полностью адекватную заданной системе как в кинематическом смысле (равны соответствующие перемещения), так и в статическом (равны соответствующие реакции в реальных и виртуальных связях). Обозначим неизвестные буквами Z_i.

Z₃ Z₄

F F₁ G

G₁ 2 Z₆

P₂

P₂

Эквивалентная система

D D₁ P₁ E E₁ Z₁ P₁ Z₅ Z₂

Заданная система

3

A B 1

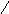
3 4 6 1 1

D=6; U_ш=8

1 2

2 2

Шарнирная модель

5

Основная система

1. 1

Вычислим реакции в виртуальных связях, вызванные угловыми и линейными перемещениями Z_i, а также внешними заданными нагрузками 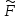, используя принцип суперпозиции. Для связи i получаем в эквивалентной системе:

где – реакция в связиi, вызванная действием единичного перемещения j связи ,- реакция всвязиi от действия внешней нагрузки .

Так как в заданной системе виртуальные связи отсутствуют, то для нее .

На основе адекватности эквивалентной и заданной систем получаем , т.е..

Раскрывая по всем i, получаем систему канонических уравнений метода перемещений:

Реакции в основной системе от различных воздействий могут быть найдены методом сил. Встречаются два основных случая опирания балок:

1. Глухие заделки с двух сторон;

2. Одна глухая заделка и одно шарнирное опирание.

А В

А В

В качестве примера рассмотрим определенные реакций, возникающих при повороте заделки А на угол .

Балка 2 раза статически неопределима n=R-U=4-2=2.

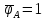
M_A M_B

з.с.

R_A R_B

о.с.

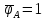
х₁

э.с. х₂

1 _Е.С., 1 _{Е. Эп.}

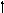
2 _Е.С., 2 _{Е. Эп}

1

1 l*1

1 г.с.

Выбираем основную систему метода сил, отбрасываем связи в опоре В, и показываем эквивалентную систему. Записываем систему канонических уравнений:

Рассматриваем 1 и 2 единичные и грузовое состояние основной системы. В роли внешней нашрузки выступает угол поворота левой опоры. Вычислим податливостии перемещения∆_iF.

Подставляем в систему:

или

Из уравнений равновесия находим:

По полученным данным строится эпюра изгибающий моментов в заданной балке от единичного угла поворота.

1 Эп.

Эпюра построена на растянутых волокнах.

Рассмотрим действие на балку силы Р.

Р

Заданная система

Основная система

P/2 P/2

x₁ x₁

Эквивалентная система

1

Pl/4

P/2

Pl/8

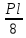
Мы получили два элемента библиотеки базовых случаев нагружения. Аналогично найдены решения для других случаев, которые как «кирпичики» используются при расчете рам.

Рассмотрим I единичное и грузовое состояния основной системы.

P₂

P₁

M_F

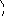
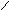
r₁₁

D

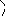
Для показанной выше рамы, например, можно записать:

где h и l – длины стоек и ригелей, сходящихся в узле D; Y_c и Y_p – моменты инерции стоек и ригелей. Аналогично находим:

После нахождения «единичных» r_ij и грузовых R_iF реакций решается система уравнений относительно перемещений узлов Z_i. Затем строится окончательная эпюра изгибающих моментов.

где – эпюра изгибающих моментов в основной системе метода перемещений от единичного перемещения- то же от внешней нагрузки.

Аналогично методу сил, в методе перемещений имеется целый ряд промежуточных и окончательных проверок правильности решения задачи.