Вопрос 2. Оптимизация инвестиционного портфеля в соответствии с теорией Шарпа.

 

Выведенные Марковицем правила построения границы эффективных портфелей позволяет находить оптимальный (с точки зрения инвестора) портфель для любого количества ценных бумаг в портфеле. Основной сложностью применения метода Марковица является большой объем вычислений, необходимый для определения весов W_i каждой ценной бумаги. Действительно, если портфель объединяет n ценных бумаг, то для построения границы эффективных портфелей необходимо предварительно вычислить n значений ожидаемых (средних арифметических) доходностей  каждой ценной бумаги, n величин дисперсий всех доходностей и n(n-1)/2 выражений ковариаций  акций в портфеле. При увеличении числа ценных бумаг в портфеле, количество необходимых значений ковариаций становится непомерно большим. Например, при 100 ценных бумаг в портфеле необходимое количество исходных данных превысит 5000.

В 1963  году  американский экономист У. Шарп (William Sharpe) предложил новый метод построения границы  эффективных  портфелей, позволяющий существенно сократить объемы необходимых вычислений.

Общее описание модели У. Шарпа. В основе модели  Шарпа лежит метод линейного регрессионного анализа, позволяющий связать две случайные зависимые переменные величины X и Y линейным выражением типа:

 

Y =  + X

 

В модели Шарпа переменной Х считается величина какого-то рыночного показателя. Сам Шарп в качестве такой переменной рассматривал доходность рыночного портфеля . В  качестве переменной Y берется отдача  какой-то i-ой акции портфеля. Представленное выше уравнение называется уравнением линейной регрессии, а коэффициенты  и считаются параметрами линейной регрессии.

Если задана длительность холдингового периода и известны значения индекса (например, РТС) I в начале I_{начальн.} и в конце I_{конечен.} холдингового периода, то доходность рыночного портфеля за этот период находится по формуле:

 

 

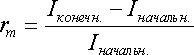
Построение регрессионной модели. Предположим, что портфель формируется из рассмотренных ранее акций фирм «А», «В» и «С». Пусть задана длительность будущего холдингового периода (для последующего сравнения модели Шарпа с моделью Марковица будем полагать, что эта длительность совпадает с выбираемой длительностью в модели Марковица) и заданы N = 10 шагов расчета в прошлом. На основании данных об изменениях рыночного индекса вычислим  доходность  рыночного портфеля за N шагов расчета. Полученные данные внесем в таблицу 7, где также приведены доходности  акции С, вычисленные ранее:

 

Таблица 7.

 

Условные доходности рыночного портфеля и акции с

 

 

В таком случае для акции С уравнение линейной регрессии должно принимать вид:

 

 = 

 

Ниже будут вычислены параметры линейной регрессии для акции С: =0,1165 и =0,5255. Значит, для этой акции уравнение линейной регрессии должно иметь вид:

 

 = 0,1165 + 0,5256 

 

Сравним получаемые по этой формуле теоретические величины  и реально наблюдаемые значения , приведенные в таблице 7:

 

 = 0,1165 + 0,5256× = 0,1165 + 0,5256×0,121 = 0,1802,

 

что отличается от наблюдаемого значения = 0,110. Чтобы уровнять теоретическую и реальную величины, необходимо провести коррекцию теоретической величины . Достигается это путем добавления к значению ошибки = 0,0702:  (0,1802  0,0702 = 0,110).

Поскольку величины  и  случайные, то, скорее всего, и остальные теоретические значения , получаемые с использованием уравнения линейной регрессии, будут отличаться от реально наблюдаемых величин , приведенных в таблице 7. В этой связи величины необходимо корректировать ошибкой на каждом шаге расчета. Так как величины  и  случайные, то и значения ошибки также должны представлять собой случайные величины. В итоге уравнение линейной регрессии для акции С должно иметь следующий вид:

 

 = + ,

          где:

          - случайная ошибка.

 

В общем случае, если в портфель включено n акций, то для любой i-ой акции портфеля уравнение линейной регрессии выглядит следующим образом:

 

 =  ,

 

          где:

           - доходность i-ой акции портфеля за шаг t;

           - параметр регрессии, называемый коэффициентом «альфа»; показывает, какая часть доходности i-ой акции портфеля не связана с изменениями доходности рыночного портфеля ;

           - параметр  линейной регрессии,  называемый коэффициентом "бета", показывающий чувствительность доходности  i-ой акции портфеля к изменениям рыночной доходности ;

           - доходность рыночного портфеля в момент t;

           - случайная ошибка,  свидетельствующая о том,  что реальные, действующие значения  и   отклоняются от линейной зависимости.

 

Уравнение =  является основным в линейном регрессионном анализе и берется за основу в модели Шарпа. В линейном регрессионном  анализе  полагается, что средняя арифметическая (ожидаемая) величина ошибок наблюдения E( )=0, то есть фактические величины  в среднем равномерно  распределяются выше  и  ниже  значений,  получаемых при линейной регрессии.

Параметр бета. Особое значение необходимо уделить параметру , поскольку он определяет чувствительность доходности i-ой акции портфеля  к изменениям рыночной доходности.  Коэффициент  для каждой ценной бумаги показывает, на сколько процентов изменится доля , определяемая воздействием рынка ( × ), при изменении рыночной доходности на 1%.

В общем случае, если >1, то доходность данной ценной бумаги более чувствительная, подвержена большим колебаниям, чем рыночная доходность r_m. Соответственно, при <1 ценная  бумага имеет меньший размах отклонений доходностей r_j от средней арифметической (ожидаемой) величины E(r_i), чем рыночная доходность. В этой связи ценные бумаги с коэффициентом >1 классифицируются как более рискованные, чем рынок в целом, а с <1 - менее рискованными, чем рынок в целом.

Как показывают исследования,  для большинства  ценных  бумаг коэффициент >0, хотя могут встретиться ценные бумаги и с отрицательной величиной . В последнем случае доходности этих ценных бумаг отрицательно коррелированны с доходностью рыночного портфеля. Следует учитывать, что и в случае отрицательных величин , если величина этого коэффициента по модулю превосходит единицу, то есть  (например, = 1,5), то акции считаются более рискованными, чем рынок в целом.

Поскольку коэффициент характеризует зависимость доходности исследуемой акции и рыночного портфеля, то, очевидно, что данный коэффициент отражает только систематическую, недиверсифицируемую часть риска.

Определение параметров  и  регрессионной модели и оценка результатов регрессии. Для нахождения параметров  и  по результатам  наблюдений используется метод наименьших квадратов (МНК).  По этому методу в качестве параметров  и  берутся такие значения, которые минимизируют сумму квадратов ошибок ,  то есть которых величина:

 

 

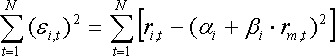
достигает минимума. Если провести необходимые вычисления, то окажется, что выражение имеет минимум, когда параметры  и  принимают следующие значения:

 

 

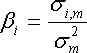
Если будут известны наблюдаемые в течение N лет  величины  и ,  то, пользуясь известными формулами для вычисления ожидаемых доходностей, ковариаций и дисперсий,  можно найти E(r_i), E(r_m), и , подставить их в выше представленные формулы и вычислить параметры регрессии  и .

Найдем значения коэффициентов  и для  акций "А", "В" и "С":

 

 =0,2494 и  = 0,9787

 = 0,0117 и =0,9470

 = 0,1165 и = 0,5256

 

Вычисление дисперсий случайной ошибки. Поскольку для определения оптимального портфеля с использованием модели Шарпа понадобятся значениядисперсий  случайных ошибок, то проведем необходимые вычисления. Общая формула для вычисления дисперсии случайной ошибки имеет вид:

 

 = 

 

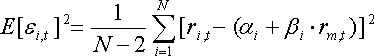
Для акций "А" вычисления дают:

 

 = [(0,1200,2694+0,97870,1212) +(0,0400,2694+0,97870,2924) +(0,0100,2694+0,97870,1479) +

+ и т.д. по всем 10 годам] / 8 = 0,0073

 

Соответственно: =0,0136 и =0,0375.

Для наглядности сведем данные регрессионного анализа для акций "А", "В" и "С" в одну таблицу (табл. 8.):

 

Таблица 8.