Стохастическое доминирование.

Стохастическое доминирование 1-ого рода:

Если распределение F первично стохастически доминирует распределение G, то при распределении выигрышей F мат. ожидание выигрыша будет больше, чем при распределении G и ожидаемая полезность будет больше( Eu(F) > Eu(G) )

Стохастическое доминирование 2-ого рода:

Распределение F вторично стохастически доминирует распределение G, если при одинаковом мат. ожидании дисперсия выигрышей G больше.

Стохастическое доминирование первого рода.

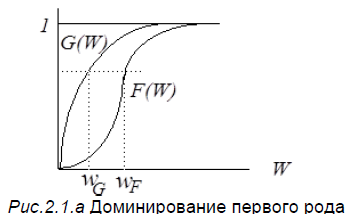
Рассмотрим два распределения F(W) и G(W)(см. рис(2.1.а).

С одной стороны, с некоей заданной вероятностью можно получить выигрыш

W ≤ wF - при распределении F и W ≤ wG - при распределении G . Т.к. F(W ) ≤ G(W ) для любого W, то, следовательно, wF > wG , что позволяет оценивать распределение F как менее рискованное. Иначе, более корректно, эту мысль можно сформулировать, указав на стохастическое доминирование распределения F распределения G.

Def. Распределение F(W) первично стохастически доминирует распределение G(W) (F(W) first-order stochastically dominates G(W)), тогда и только тогда, когда F(W ) ≤ G(W) для любого W.

Соответственно, если распределение F первично стохастически доминирует

распределение G, то

• при распределении выигрышей F математическое ожидание выигрыша

будет выше чем при распределении G:

Графически это может интерпретироваться следующим образом(простоты ради зададим в данном случае совпадающие интервалы выигрышей):

• при распределении выигрышей F ожидаемая полезность будет выше, чем при распределении G, т.е. для любой неубывающей функции u(W) выполняется условие

Несмотря на то, что стохастическое доминирование первого рода позволяет нам проранжировать лотереи как по уровню математического ожидания выигрыша, так и по уровню их ожидаемой полезности, обратное неверно, т.е. ни по уровню математического ожидания выигрыша , ни по уровню ожидаемой полезности нельзя делать вывод о стохастическом доминировании первого рода, поскольку ранжирование лотерей с точки зрения доминирования первого рода является частичным. Например, распределение G(W ) первично стохастически доминируется распределениями F(W) и F '(W), но не существует возможности,

рассматривая лишь доминирование первого рода, проранжировать эти два последние распределения.

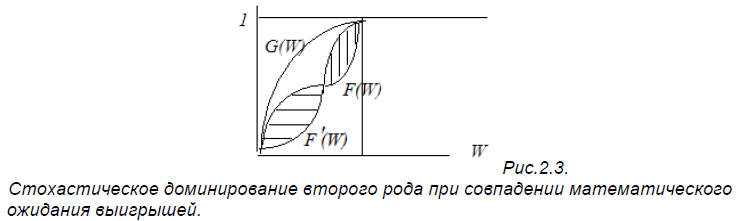
Несколько упрощая рассмотрение стохастического доминирования второго рода, сконцентрируемся лишь на тех распределениях, которые характеризуются совпадением математических ожиданий выигрышей.

Итак, две игры могут иметь одно и тоже математическое ожидание выигрыша, но различаться в степени своей рискованности. Например, игра, в которой с вероятностью 1/2 можно выиграть и с вероятностью 1/2 проиграть h долларов всегда будет менее рискованной чем игра, где с равными вероятностями можно выиграть или проиграть 2 h долларов. В подобном случае уместно говорить о стохастическом доминировании второго

рода или вторичном стохастическом доминировании.

Def. Распределение F(W) вторично стохастически доминирует

распределение G(W) ( F(W) second-order stochastically dominates G (W) ),

имеющее такое же математическое ожидание

если распределение G предполагает больший разброс выигрышей, т.е. его

дисперсия больше.

Пример. Сравним две игры, имеющие распределение G(W) и F(W) .В первой игре с вероятностями 0.25 можно выиграть 1, 2, 3 и 4. Во второй с вероятностями 0.5 можно получить 2 и 3. В обоих случаях математическое ожидание одинаково - 2.5 , что графически иллюстрируется совпадением площадей заштрихованных фигур.

Но поскольку в распределении G(W) задан больший разброс выигрышей, т.е. его дисперсия выше, чем при распределении F(W), оно является более рискованным.

Без доказательства приведем теорему, гласящую, что, если распределение F(W)вторично стохастически доминирует распределение G(W), то для любой возрастающей вогнутой функции полезности u(W) выполняется условие

Достоверный эквивалент лотереи, рисковая премия, рисковая

нагрузка, вероятностная премия.

Достоверным эквивалентом лотереи l называется величина l^ такая, что f(l^)=Ml[f] (полезность l^ равна ожидаемой полезности l). Т.е. для ЛПР безразлично, получить l^ наверняка или участвовать в лотерее l. Достоверный эквивалент единственен, т.к. f монотонная.

Рисковая премия (risk premium), обозначаемая в дальнейшем r, представляет собой максимальную плату, которую не склонный к риску индивид готов заплатить за то, чтобы избавиться от предстоящей ему справедливой игры, и , соответственно, равна разности между математическим ожиданием выигрыша E(W) и величиной достоверного

эквивалента игры (c):

Рисковая премия - часть страховой премии, которая расходуется страховщиком на создание необходимого фонда оплаты сумм страхового возмещения. Премия за риск неполучения доходов, предусмотренных основным сценарием проекта, определяется из условия равенства между

ожидаемым эффектом проекта, рассчитанным при безрисковой норме дисконта, и эффектом основного сценария, рассчитанным при норме дисконта, включающей поправку на риск. Разность между ожидаемым выигрышем и ценой продавца(достоверным эквивалентом лотереи) - премия

за риск.

Нагрузка (рисковая??) - часть страхового тарифа, предназначенная для покрытия затрат на проведение страхования и создания резерва (фонда) предупредительных мероприятий. В составе нагрузки может быть предусмотрена прибыль от проведения страховых операций.

Рисковая нагрузка - Можно добиться безразличия не склонного к риску индивида между гарантированным обладанием W0 и рискованными инвестициями, имеющими такое же математическое ожидание выигрыша, предложив ему денежную компенсацию l = W* - W0 за принятие этой справедливой игры. При этом вполне логичным представляется интерпретация подобной величины рискового вознаграждения или

рисковой нагрузки( в англоязычной литературе называемой risk loading) как готовности индивида принимать компенсацию (WTA) или же компенсирующей вариации дохода, подобно тому как рисковая премия r т.е.плата, которую индивид готов заплатить за то, чтобы избежать уготованной ему справедливой игры, интерпретировалась нами как

эквивалентная вариация дохода или готовность платить(WTР).

При фиксации уровня выигрышей, повышение математического ожидания выигрыша может быть достигнуто за счет приращения вероятности получения лучшего приза. Подобное приращение вероятности , делающее не склонного к риску индивида безразличным между участием и неучастием в игре: получило название вероятностной премии.