Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Институт экономики и финансов КФУ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

matan_baza

.pdf

Скачиваний:

Добавлен:

02.06.2015

Размер:

3.39 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 153 4 5 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

параллельна плоскости xOy совпадает с плоскостью xOy перпендикулярна оси Oz

33.Вектор N (3; 1; –2)

параллелен плоскости 3x + y – 2z + 5 = 0

образует с плоскостью 3x + y – 2z + 5 = 0 острый угол лежит в плоскости 3x + y – 2z + 5 = 0 перпендиклярен плоскости 3x + y – 2z + 5 = 0

34.Уравнение 3x 4y 2z 1 определяет

прямую кривую линию плоскость эллипс

35.Среди прямых:

1)	x 3		y 1			z 2			,

	5		3		4
2)		x 3		y 1			z 2			,

	4		3		5
3)		5 x		y 2				4 z		,
		4	3					5

4)		x 1		y 2			z 1
		4	3
								5

параллельными являются

3) и 4)

2) и 3)

1)и 2)

2)и 4)

1)и 4)

36.Среди прямых:


1)	x 1		y 2				z 2			,

	2			3		1
2)		x 1			y 2				z 2		,

	2			3		2
3)		x 5			y 1			z 4			,
					2
	0,5					5

4)x 3 y 5 z 1 4 1 6

Взаимно перпендикулярными являются

1)и 3)

1)и 2)

1)и 4)

2)и 4)

2)и 3)

37. Прямая	x 2	y 1		z 1	и плоскость 1,5x + y + 2z + 1 = 0

	3	2	4

параллельны образуют угол в 45˚

взаимно перпендикулярны образуют угол в 30˚

38. Прямая	x	y 1		z 2	и плоскость 3x + 4y + 6z – 2 = 0
		3
	2		1

взаимно перпендикулярны образуют угол в 45˚ образуют угол в 30˚ параллельны

39.Косинус угла между плоскостями 2y + z – 5 = 0 и x – 2y + 3 = 0 равен

0,4

–0,8

–0,2 0,6

–0,4

40.Косинус угла между плоскостями 2x + y – z + 4 = 0 и x – y + 2z – 1 = 0 равен

– 13 1

– 16 1

41.Расстояние от точки M0 (1 ; 1 ; 4) до плоскости 2x + 2y – z + 6 = 0 равно

42.Расстояние от точки M0 (0 ; –2 ; 3) до плоскости 2x – 6y + 3z = 0 равно

43. Расстояние от точки M0 (4 ; –2 ; 0) до плоскости 3x – 2y + 3 z + 4 = 0 равно

44.	Косинус угла между прямыми	x 1		y 2		z 1	и		x		y 1			z 2				равен
44.	Косинус угла между прямыми					2	и											равен
		2	1			2		2				6			3
4

21
4

23
5

29
3

11
5

19
45.	Косинус угла между прямыми	x 3		y 1		z 2	и		x 2				y 1				z		равен
45.	Косинус угла между прямыми						и												равен
		9	2		6					2			1			2
7

– 225 8

– 416

46. Уравнения прямой, проходящей через точки M1 (2 ; –3 ; 1) и M2 (–1 ; 4 ; 2):

x 1	y 4			z 2
		3
2			1
x 2		y 3			z 1
3
	7		1
x 2		y 3			z 1
1
	4		2
x 1	y 4			z 2

4	9		1
x 2		y 3			z 1
3
	7		1

47. Уравнения прямой, проходящей через точки M1 (3 ; 5 ; –4) и M2 (2 ; –1 ; 3):

x 3	y 5			z 4
	1
2		3
x 2	y 1			z 3
3	5			4

x 2	y 1			z 3
1	6			7

x 3	y 5			z 4
	1
2		3
x 2	y 1		z 3
3	5
				4

48.Параметрические уравнения прямой, проходящей через точку M0 (2 ;

5 ; –3) параллельно вектору l (4; –1; 6) имеют вид

x 4 2t,y 1 5t,

z 6 3t

x 4 2t,y 1 5t,

z 6 3t

x 2 4t,y 5 t,

z 3 6t

x 2 4t,y 5 t,

z 3 6t

2x 5y 3z 04x y 6z 0

49.Синус угла между прямой

1 = 0 равен

– 1321 7

–238

–17

x 5	y 3		z 1	и плоскостью 6x + 3y – 2z +
2
	1	2

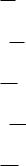
50. Синус угла между прямой	x 4	y 3	z 1	и плоскостью 2x – y + 2z – 3
	6	9	2

= 0 равен

–117 1

– 331 5

51.Установить соответствие:

A.	x 1			y 2					z 3		;	1.	Проходит через точку M0 (1 ; 2 ; 3);
A.	3		4						2		;	1.	Проходит через точку M0 (1 ; 2 ; 3);
	3		4						2
B.		x 2			y	z 1				;			2. Параллельна плоскости 3x + 4y – 2z =
B.										;			2. Параллельна плоскости 3x + 4y – 2z =
	5		2				4
0;
C.		x 5			y 3		z 2 ;					3.	Перпендикулярна плоскости 3x + 4y – 2z –
C.		4		2			z 2 ;					3.	Перпендикулярна плоскости 3x + 4y – 2z –
		4		2
1 = 0;
D.		x 1			y 1			z 3			;	4.	Проходит через точку M0 (2 ; 0 ; –1);
D.		1									;	4.	Проходит через точку M0 (2 ; 0 ; –1);
		1	3				2
												5.	Перпендикулярна плоскости –4x + 2y + z –
3 = 0;
												6.	Параллельна прямой x	y 2	z 1
												6.	Параллельна прямой x	3	2
														3	2

A-1, B-4, C-2, D-6

A-3, B-4, C-5, D-6

A-2, B-6, C-5, D-1

A-6, B-5, C-3, D-1

52.Установить соответствие:

A. 2x + y – 3z + 3 = 0;		1. Параллельна прямой	x	y	z 3	;
A. 2x + y – 3z + 3 = 0;		1. Параллельна прямой			3	;
		2		1	3
B. 6x – 5y – 7z = 0;	2.	Проходит через точку M0 (–1 ; 2 ; 1);
C. 6x – 5y – 7 = 0;	3.	Параллельна оси Oz;
D. y – 3z = 0;	4.	Параллельна плоскости xOy;

5.Проходит через начало координат;

6.Проходит через ось Ox

A-1,B-4,C-5,D-2

A-2,B-5,C-3,D-6

A-1,B-3,C-6,D-5

A-3,B-1,C-2,D-4

53.

Установить соответствие:

A. 3x – 5y + z = 0;	1.	Проходит через ось Oy;
B. 4x + 3y – 7 = 0;	2.	Параллельна плоскости xOz;
C. 2x + 7z = 0;	3.	Проходит через начало координат;
D. 9y – 2 = 0;	4.	Параллельна оси Oy;

5. Параллельна оси Oz;

6. Параллельна плоскости xOy

A-3,B-6,C-2,D-4

A-3,B-5,C-1,D-2

A-6,B-4,C-2,D-3

A-2,B-5,C-4,D-6

54.Установить соответствие:

A. 2x + 5 = 0;	1.	Проходит через начало координат;
B. 3y – 4z = 0;	2.	Параллельна плоскости xOy;
C. x + 2y – 3z = 0;	3.	Параллельна плоскости yOz;
D. 4x – 3y + 5 = 0;	4.	Проходит через ось Oz;

5. Параллельна оси Oz;

6. Проходит через ось Ox

A-6,B-3,C-4,D-1

A-2,B-6,C-1,D-4

A-3,B-6,C-1,D-5

A-1,B-5,C-2,D-4

55.Установить соответствие:

A. 6x + 7y = 0;	1.	Параллельна оси Ox;
B. 2y + 3z – 1 = 0;	2.	Проходит через ось Oz;
C. 3z – 5 = 0;	3.	Параллельна плоскости yOz;
D. 4x – y + 6z = 0;	4.	Параллельна плоскости xOy;

5. Проходит через начало координат; 6. Проходит через точку M0 (1 ; 1 ; 1)

A-4,B-3,C-2,D-6

A-3,B-5,C-2,D-1

A-6,B-4,C-5,D-1

A-2,B-1,C-4,D-5

Тема: 3. Пределы последовательностей и функций

1.Если lim (x) 0, то функция (х) называется

x 3

бесконечно большой функцией в точке х=3 бесконечно малой функцией в точке х=3 постоянной в точке х=3 убывающей функцией в окрестности х=3

2.Если бесконечная числовая последовательность an имеет предел а, то

–окрестность точки а содержит бесконечное число членов последовательности

конечное число членов последовательности бесконечно малое число членов последовательности ровно n членов

3.Предел	x 1	2x2 x 3	равен
		3x2 2x 1
	lim

4 54 4

5 54

4.Какое из утверждений верно?

Если последовательность имеет предел, то она монотонна Если последовательность монотонна, то она сходится

Если последовательность монотонна и ограничена, то она имеет предел Если последовательность сходится, то она знакопостоянна

5.Выражение равно 0 равно равно –

является неопределенностью

6.Если	lim f (x) , то функция f (x) называется
	x x0

бесконечно малой величиной в точке х= x0 бесконечно большой величиной в точке х= x0 непрерывной в точке х= x0

константой

7.Предел	Lim	sin	равен


	0

–1

8.Предел постоянной C 0 равен

самой постоянной другой постоянной

9.Предел произведения двух функций равен сумме пределов этих функций разности пределов этих функций произведению пределов этих функций отношению пределов этих функций

10.Для существования предела функции f (x) в точке x0 , равного числу a 0, необходимо и достаточно, чтобы в некоторой окрестности точки x0

при условии, что f (x) (x)

f (x) a (x) f (x) a (x)

f (x) a

(x)

11. Предел lim 1

2 e

(x) – бесконечно малая функция в точке x0

1 n равен n

12. – окрестностью точки а называется интервал длиной с центром в точке а интервал длиной 2 с центром в точке а интервал длиной 2 , содержащий точку 0 интервал длиной с центром в нуле

13. Если бесконечная числовая последовательность {an } имеет предел а,

то вне - окрестности точки а содержится конечное число ее членов бесконечное число ее членов фиксированное число членов

ровно n членов

14. Предел	lim	2x 2	7x 3	равен
		3x 2	10x 3
	x 3

	5
	8
	8
0
			5	3n 1
15. Предел		lim 1		равен
15. Предел		lim 1		равен
		n	n

e15 5

e 3

e 15 e 53

16. Если члены последовательностей {an }, {bn }, {cn } при любых n N

удовлетворяют неравенствам an bn cn и lim an lim cn a , то

n n

lim bn	a
n
lim bn	a
n
lim bn	a
n
lim bn	a
n
17. Если lim an		a , lim bn	b	и для любых	n N выполняется неравенство
	n	n

an bn , то a=b

a<b a b a b

			1 5n
18. Предел		lim 1		равен
		lim 1
		n	3n
	5
	3
e	3
5

e 3
e15
3

e 5

19. Предел	lim	2x3	x2 3	равен
19. Предел	lim	3x2	x 2	равен
	x	3x2	x 2
2

3

20. Предел

21. Предел

22. Предел

23. Предел

24. Предел

e 3 e


lim	3x2		x 2	равен
		11x 3
x 4x2

lim	3x2	5x 7
		2x 5 равен
x 4x3

lim	sin 3x	равен
	x
x 0

sin x

lim 2 равен

x 0 x

	3 x
lim 1		равен

x	x

<<< < Предыдущая 1 23 / 153 4 5 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.06.20151.56 Mб13LinAlg_dnev_12_13.pdf
#
02.06.2015878.41 Кб17LinAlg_dnev_13_14.pdf
#
02.06.2015997.56 Кб282Makro_otvety_2011-2012 (1).pdf
#
02.06.201528.7 Mб365Man to Man.pdf
#
02.06.2015452.53 Кб5Manuscript.pdf
#
02.06.20153.39 Mб21matan_baza.pdf
#
02.06.20152.83 Mб64matan_individualki.doc
#
02.06.20151.01 Mб50metodichka_FUFO_novaya.doc
#
02.06.2015494.59 Кб186mikra_s_otvetami (1).doc
#
02.06.2015195.82 Кб52Mikroekonomika_Ekzamen_33.docx
#
02.06.2015270.85 Кб12OPORNYJ_KONSPEKT_-_2013.doc

x 1	y 4			z 2
		3
2			1
x 2		y 3			z 1
3
	7		1
x 2		y 3			z 1
1
	4		2
x 1	y 4			z 2

4	9		1
x 2		y 3			z 1
3
	7		1

x 3	y 5			z 4
	1
2		3
x 2	y 1			z 3
3	5			4

x 2	y 1			z 3
1	6			7

x 3	y 5			z 4
	1
2		3
x 2	y 1		z 3
3	5
				4

x 1	y 4			z 2
		3
2			1
x 2		y 3			z 1
3
	7		1
x 2		y 3			z 1
1
	4		2
x 1	y 4			z 2

4	9		1
x 2		y 3			z 1
3
	7		1

x 3	y 5			z 4
	1
2		3
x 2	y 1			z 3
3	5			4

x 2	y 1			z 3
1	6			7

x 3	y 5			z 4
	1
2		3
x 2	y 1		z 3
3	5
				4

x 1	y 4			z 2
		3
2			1
x 2		y 3			z 1
3
	7		1
x 2		y 3			z 1
1
	4		2
x 1	y 4			z 2

4	9		1
x 2		y 3			z 1
3
	7		1

x 3	y 5			z 4
	1
2		3
x 2	y 1			z 3
3	5			4

x 2	y 1			z 3
1	6			7

x 3	y 5			z 4
	1
2		3
x 2	y 1		z 3
3	5
				4