Вопрос 10 Математическое ожидание дискретной случайной величины. Свойства математического ожидания. Дисперсия дискретной случайной величины и ее свойства.

Математическое ожидание дискретной случайной величины.

Математическим ожиданием называется

• для дискретной случайной величины:

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания)

Свойства математического ожидания

1) . Если С - постоянная величина, то МС = С

2) . МСх = СМх

3). Математическое ожидание суммы случайных величин всегда равно сумме их математических ожиданий: М(х+y) = Мх + Мy

4). Вводится понятие условного математического ожидания. Если случайная величина принимает свои значения хi с различными вероятностями p(xi/Hj) при разных условиях Hj, то условное математическое ожидание определяется

как или ;

Если известны вероятности событий Hj, может быть найдено полное

математическое ожидание: ;

5). Если f(x) - есть функция случайной величины х, то определено понятие математического ожидания функции случайной величины:

- для дискретной случайной величины: ;

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся.

-для непрерывной случайной величины: ;

Интеграл должен быть абсолютно сходящимся.

Дисперсия дискретной случайной величины и ее свойства.

Дисперсией случайной величины х называется математическое ожидание квадрата отклонения значения величины от ее математического ожидания: Dx = M(x-Mx)²

• для дискретной случайной величины: ;

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии)

Свойства дисперсии:

1) . Если С - постоянная величина, то DС = 0

2). DСх = С²Dх

3). Дисперсия суммы случайных величин всегда равно сумме их дисперсий только, если эти величины независимы (определение независимых величин)

4). Для вычисления дисперсии удобно использовать формулу:

Dx = Mx² - (Mx)²

Вопрос 11 Основные законы распределения вероятностей дискретной случайной величины: Бернулли, биномиальное, геометрическое, распределение Пуассона, (гипергеометрическое)

Распределение Бернулли

Если производится серия независимых испытаний, в каждом из который событие А может появиться с одинаковой вероятностью р, то число появлений события есть случайная величина, распределенная по закону Бернулли, или по биномиальному закону (другое название распределения).

Здесь n - число испытаний в серии, m - случайная величина (число появлений события А), Р_n(m) - вероятность того, что А произойдет именно m раз, q = 1 - р (вероятность того, что А не появится в испытании).

Пример 1: Кость бросают 5 раз, какова вероятность того, что 6 очков выпадет дважды ?

n = 5, m = 2, p = 1/6, q = 5/6

Параметры распределения: n , р

Биномиальный закон распределения. Случайная величина X принимает значения О, 1, 2, 3, 4, 5,..., n, с вероятностью, определяемой по формуле Бернулли (1.10.1):

xi	0	1	2	…	k	…	n
pi				…		…

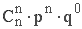
Геометрический закон распределения.

Пусть Р(А)=р - вероятность наступления события А в каждом опыте, соответственно, q=l-p - вероятность не наступления события А.

Вероятность наступления события А в k-ом опыте определяется по формуле:

Случайная величина X, распределенная по геометрическому закону принимает значения 1, 2,..., k,... , с вероятностью, определяемой по формуле:

x_i 1 2 3 ... k ...

p_i p pq pq² ... pq^k-1 ...

Гипергеометрический закон распределения.

Пусть в урне N-шаров, из них М белых, а остальные (N - М) черные. Найдем вероятность того, что из извлеченных n шаров m белых и (n-m) черных.

N = М + (N-M);

n = m + (n-m);

-- число способов выбора m белых шаров из М;

-- исло способов выбора (n-m) черных шаров из (N-M). По правилу произведения, число всех возможных наборов из m белых и (n-m) черных равно

-- бщее число способов выбора из N шаров n.

Отсюда, по формуле классического определения вероятности:

Ограничения на параметры: М £ N, m £ n; m = m₀, m₀₊₁, m₀₊₂,..., min(M,n), где m₀=max{O, n-(N-M)}. Случайная величина Х, распределенная по гипергеометрическому закону распределения (при m=0, 1, 2, 3,..., М), имеет вид:

xi	0	1	2	…	m	…	M
pi				…		…

Гипергеометрический закон определяется тремя параметрами N, М, n. При n<0,1N этот закон стремится к биномиальному.