Ответы ТВ И МС Ответы на Билеты 1-26( 2008-2009 уч. год)
.doc|
1) Дать определение основных видов событий, полной группы событий, произведения и суммы событий. Сформулировать ассоциативный, дистрибутивный и коммутативный законы применительно к операциям над событиями. Случайное событие – явление, которое может произойти или нет при осуществлении опыта. Опыт (испытание)- всякое осуществление определенного комплекса условий (S), при котором можно наблюдать некоторые явления. Если при осуществлении комплекса условий событие не может произойти, то оно называется невозможным (Ø). Если при осуществлении комплекса условий событие обязательно произойдёт, то оно называется достоверным (Ω). Событие А влечет за собой событие В (А с В), если при наступлении А наступает и В. Произведением событий А и B называется событие C, которое означает, что одновременно осущ-ся и А и B. Суммой соб. А и B нзв соб.C, которое означает осущ-е хотя бы одного из соб. А или B. Несовместные события – если произведение 2-х событий есть невозможное событие. Множество (W) всех элементарных исходов данного опыта называется пространством элементарных исходов (событий). События А и В называются противоположными, если для них одновременно выполняется: 1) А*В=Ø; 2) А+В = Ω Полная группа событий – множество попарно несовместных событий, сумма которых есть достоверное событие. Операции с событиями: 1) Коммуникативный закон: А+В=В+А 2) Ассоциативный: А+(В+С)=(А+В)+С, А*(В*С)=(А*В)*С 3) Дистрибутивный А(В+С)=АВ+АС
2. Дать определение классического эксперимента. Классическое, статистическое, геометрическое и аксиоматическое определения вероятности. Классический эксперимент – эксперимент, который приводит ко множеству элементарных событий, которые попарно несовместны, образуют полную группу событий и они равновозможные. Равновозможными называются события, если нет основания полагать, что одно событие вероятнее другого. Классическое: Вероятностью появления события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных и несовместных элементарных исходов. Статистическое: Статистической вероятностью события А называется относительная частота (частость) этого события, вычисленная по результатам большого числа испытаний. Будем
обозначать ее Р*(А).
Следовательно Геометрическое: называют отношение площадей. Р(А)= Sg/SG Аксиоматическое определение вероятности: f є F F:
1). ΩєF ; 2).
Множество F устроенное таким образом называется полем событий (fєΣwi). Аксиома 1. Каждому случайному событию А из поля F может быть поставлено в соответствие неотрицательное число Р (А), называемое его вероятностью. Аксиома 2. Р(Ω)=1. Аксиома 3. Если события А1, А2, …, Ап попарно несовместны, тогда вероятность их суммы: Р(А1+А2+…+Ап)=Р(А1)+Р(А2)+…+Р(Ап) {Ω,F,Ρ} – вероятностное пространство Следствие
1: Для А
0≤Р(А) ≤1; Следствие
2: Для
всех А Р( Следствие 3:Р(Ø)=0;Следствие 4: Если А с В =>Р(А) ≤ Р(В)
3. Сформулировать два основных правила комбинаторики. Формулы числа перестановок, сочетаний и размещений. Формула подсчета вероятностей в «Урновой схеме». Правило умножения: Если объект А может быть выбран n способами, а объект В – m способами, то выбрать одновременно и А, и В можно n*m способами. Правило сложения: Если объект А может быть выбран n способами, а объект В – m способами, то выбрать или А, или В можно n+m способами. 1). Число перестановок Рn=n! 2). Размещение с повторениями
3). Размещение без повторения
4). Число сочетаний
5). Число сочетаний с повторениями
«Урнова схема»: Пусть есть N элементов, из них М – 1 сорта, N-M – 2 сорта. Из урны извлекаются n-элементов. Вероятность того, что m будет 1 сорта:
4. Теоремы сложения для совместных и несовместных событий (без доказательства). Определение условной вероятности. Теорема умножения для зависимых и независимых событий (без доказательства). Теоремы сложения: Р(А+В+С)=Р(А)+Р(В)+Р(С)-Р(АВ)-Р(АС)-Р(ВС)+Р(АВС) Р(А+В)=Р(А)+Р(В)-Р(АВ) – для совместных Р(А+В)=Р(А)+Р(В) – для несовместных Теорема умножения: Р(АВ)=Р(А)*Р(В/А) или Р(АВ)=Р(В)*Р(А/В) Р(АВ)=Р(А)*Р(В) – для независимых Р(АВ)=Р(А)*РА(В) Условная вероятность: РА(В)=Р(АВ)/Р(В) Вероятность наступления события В при наступлении события А.
5. Дать определение гипотез. Формулы полной вероятности и Байеса (без доказательства). Пусть событие А может наступить только одновременно с одним из n событий Нi, образующих полную группу. Тогда Нi называются гипотезами. Формула полной вероятности: Р(А)=Р(Н1)*Р(А/Н1) + Р(Н2)*Р(А/Н2) +…+ Р(Нn)*Р(А/ Нn) Формула Байеса: Пусть событие А может наступить только совместно с 1 из гипотез Нi, Относительно которых известны их вероятности Р(Нi). Нам известна условные вероятности события А, при условии наступления этих гипотез. Пусть событие А наступило, тогда мы можем переоценить вероятность гипотез Нi: Р(Нi/А) = Р(Нi)*РА/ Нi) / Р(А)= Р(Нi)*Р(А/ Нi) / ΣР(Нj)*Р(А/Нj)
6. Определение схемы последовательных независимых испытаний. Формула Бернулли (без доказательства) Пусть проводится конечное число n последовательных независимых испытаний, в каждом из которых может произойти или не произойти некоторое событие А. Если Р(А) в каждом испытании одинаковы, то такая последовательность испытаний называется схемой Бернулли (схемой последовательных независимых испытаний).
Вероятность того, что при n испытаниях, проведенных по схеме Бернулли, событие А наступит ровно m раз. |
7. Приближенные формулы вычисления вероятности в схеме последовательных независимых испытаний и условия их применения: локальная и интегральная теоремы Муавра-Лапласа, теорема Пуассона (без доказательства) Локальная теорема Муавра-Лапласа: Если вероятность Р(А) в каждом из n независимых испытаний постоянна и не равна 0 и 1, тогда Pn(m)≈1/√npq * φ(x). A наступает m раз. φ(x)-малая функция Лапласа. Интегральная теорема Муавра-Лапласа: Если вероятность Р(А) в каждом из n независимых испытаний постоянна и р≠0 и р≠1, тогда вероятность наступления А m раз в n испытаниях на отрезке [k1;k2] Pn(k1≤m≤k2)=Ф(в)-Ф(а) Теорема Пуассона: Если в схеме последовательных и независимых испытаний вероятность Р наступления события А р→0, n→∞, λ=np≈const Pn(m)
→
n→∞
8. Определение и свойства функции распределения вероятностей (без доказательства). Определение непрерывной случайной величины, Плотность вероятности и ее свойства (без доказательства). Функция распределения вероятностей. Пусть Х – некоторая СВ, х – некое действительное произвольное число, тогда ФРВ называется вероятность, с которой CB X примет значение меньше, чем х (Р(Х<x)=F(x)) Свойства: 1). Р(х1≤X<x2)=F(x2)-F(x1) 2). 0≤F(x)≤1 3). F(x)≥0 ФРВ неубывающая 4).ФРВ непрерывна слева 5). F(-∞)=0, F(+∞)=1 6). F(x) – непрерывна CB
называется непрерывной, если для неё
существует неотрицательная функция
F(z),
которая при всех х: F(x)= F(z) называется плотностью вероятности (плотностью распределения) 1). f(x)≥0 2).
Для всех х1 и х2, Р(х1≤Х<х2)= 3).
9. Определение математического ожидания. Свойства математического ожидания. Определение дисперсии и среднеквадратического отклонения. Свойства дисперсии. Формула для вычисления дисперсии. Математическим ожиданием ДСВ называется число М(Х) = Σ xi* pi, где xi – значения x, Pi=P(x=xi). Если ряд сходится абсолютно. Если величина Х имеет бесконечное число значений, то CB имеет М(Х), если нет – то не имеет. Для
непрерывных СВ с плотностью вероятности
= f(X):
Свойства М(Х): 1). М(С)=С; 2). М(СХ)=С*М(Х); 3). М(Х+У)=М(Х)+М(У); 4). Если Х и У независимы, то М(Х*У)=М(Х)*М(У) Пусть Х – некоторая СВ, а М(Х), тогда Х-М(Х) – отклонение СВ. М(Х-М(Х))=0 Дисперсией СВ (Д(Х)) называется М[(X-M(X))²] 1). Д(Х)=Σ(xi-M(X))²*pi – в дискретном случае 2).
В непрерывном случае
М(Х) и Д(Х) – размерные. Размерность М(Х) та же, что и у СВ, а размерность Д(Х) равна квадрату размерности СВ. Среднеквадратическое
отклонение СВ Х это
Свойства дисперсии: 1). Д(С)=0; 2). Д(СХ)=С²Д(Х); 3). Д(Х+У)=Д(Х)+Д(У) Д(Х)=М(Х²)-(М(Х))²
10. Определение моды и медианы. Определение начальных и центральных моментов, квантилей и квартилей. Мода. Если Х непрерывна, то мода – точка локального максимума функции плотности распределения вероятности. Медиана. Me X=x, P(X<x)=P(X≥x)=½
Центральный момент порядка k – μk
Если х – абсолютная непрерывная СВ, то квартили делят всю вероятность на 4 равные части. Квантиль делит на р равных частей.
11. Биномиальный закон распределения и его числовые характеристики. Распределение Пуассона и его числовые характеристики. Гипергеометрическое распределение. Дискретная СВ Х обладает Биноминальным Законом Распределения с параметрами n и р, если значениями х являются натуральные числа от 1 до n, а вероятности определяются формулой Бернулли.
М(Х)=np,
Д(X)=npq,
(p+q)ⁿ-бином= Гипергеометрический
Закон Распределения.
Если Х принимает целочисленные значения
от 0 до М с вероятностью М(Х)=n*M/N, D(X)=n*M/(N-1)*(1-M/N)*(1-n/N) Распределение Пуассона. Х={количество наступлений А из n испытаний} С параметром λ, если она принимает целочисленные значения от 0 до n, где n до +∞. λ- среднее число наступлений события А. Если n=const=> λ=np M(X)=Д(X)=λ
12. Равномерное, показательное и нормальное распределения (вид плотности вероятности), их числовые характеристики. Равномерное распределение – закон распределения, который имеет постоянную плотность распределения в области значений СВ. М(Х)=(в+а)/2, Д(Х)=(в-а)²/12
Показательный (экспоненциальный) закон распределения. Если плотность СВ
Нормальный
закон распределения. СВ Х распределена
нормально (X~N(a,σ)),
если она определена на всей числовой
прямой и её плотность:
M(X)=a, Д(Х)=σ², F(X)=1/2+Ф(х-а/ σ)
13. Вид функции плотности вероятности нормально распределенной случайной величины. Свойства функции Лапласа. Вероятность попадания в интервал нормально распределенной случайной величины. (Все без доказательства).
Свойства
функции Лапласа: 1). Ф(-х)=-Ф(х); 2). Ф(х)
монотонно возрастает; 3).
Х→∞
|
14. Вероятность отклонения от математического ожидания нормально распределенной случайной величины (без доказательства). Правило «трех сигм». Определение коэффициентов ассиметрии и эксцесса.
Правило
3σ:
Ассиметрия Для нормального распределения γ=0
15. Центральная предельная теорема и ее следствия (без доказательства). Неравенство Чебышева, теорема Чебышева, теорема Бернулли (без доказательства). Пусть х1,х2,…,хn последовательность попарно независимых и одинаково распределенных СВ с конечными мат. ожиданиями и дисперсиями, тогда Д(Хi)=σ²i, M(X)i=ai Если σ²i≠0, при достаточно больших n закон распределения суммы этих СВ будет сколь угодно близок к нормальному.
Следствие1: Для всех i M(Xi)=a, Д(Xi)=σ², то X=ΣXi, тогда при достаточно больших n X~N(na,σ√n) Интегральная теорема Муавр-Лапласа является следствием из центральном предельной теоремы. P(k1≤m≤k2)=Ф(K2-np/√npq)-Ф(K1-np/√npq) М(Х)=np, Д(Х)=npq Неравенство Чебышева: для любой СВ вероятность того, что она отклонится от своего мат. ожидания не менее, чем на некоторое положительное число ε удовлетворяет неравенству:
Теорема Чебышева: Пусть х1, х2,…,хn попарно независимые СВ с конечными мат. ожиданиями, и ограничены дисперсиями, тогда если n достаточно велико среднее арифметическое этих СВ сходится по вероятности к среднему арифметическому мат. ожиданий.
n→∞ Теорема
Бернулли:
Пусть проводится n
независимых испытаний, в каждом из
которых вероятность наступления А
одна и та же и равна Р(А)=р, тогда при
увеличении количества испытаний n
относительная частота появления
события А стремится по вероятности к
вероятности события А. n→∞
16. Определение и свойства функции распределения вероятностей двумерной случайной величины. Вероятность попадания двумерной случайной величины в полуполосу и прямоугольник. (Все без доказательства) Закон распределения – перечень пар значений Xi и Yj и соответствующая им вероятность Pij Функция распределения вероятность ДСВ. F(X,Y)=P(X<x, Y<y) 1). 0≤F(x,y)≤1; 2). F(x,y) неубывающая по каждому аргументу; 3). F(x,y) непрерывна слева по каждому аргументу; 4). F(-∞;y)=0, F(x;-∞)=0, F(-∞;-∞)=0, F(+∞;+∞)=1, Д≠(x;-∞)=0, {X<x, Y<+∞}=Ǿ, {X<+∞;Y<+∞}=Ω; 5). F(X;+ ∞)=Fx(X), F(+∞;y)=Fy(Y); 6). P(x1≤X≤x2, Y=y)=F(x2,y)-F(x1,y) P(X<x, y1<Y<y2)=F(x,y2)-F(x,y1) A={X<x2,Y<y}, B={X<x1, Y<y}, C={x1≤X≤x2,Y<y}, A=B+C, B и C несовместны В*С=Ǿ С=А-В, Р(С)=Р(А)-Р(В) 7). P(x1≤X<x2, y1≤Y<y2)=F(x2,y2)-F(x1,y2)-F(x2,y1)+F(x1,y1)
17. Определение двумерной непрерывной случайной величины и ее плотности вероятности. Свойства плотности вероятности двумерной непрерывной случайной величины. (Все без доказательства) Если
двумерная функция распределения
вероятности F(x,y)
непрерывна и может быть представлена
в виде:
1). f(x,y)≥0 2). 4).
Если
F(X,Y)
2 раза дифференцируема, то из нее можно
найти плотность
18. Определение условных законов распределения для компонент двумерной дискретной случайной величины. Вычисление условной плотности вероятности. Безусловный закон распределения ДСВ – это закон распределения, не зависящий от того, какое значение примет другая компонента. Условным законом распределения компоненты Х, при условии, что компонента У приняла значение yi называется совокупность значений Х и их совместная вероятность. Условная
плотность вероятности для компоненты
Х:
19. Условие независимости компонент двумерных дискретных и непрерывных случайных величин. Понятие условного математического ожидания и регрессии. Для того, чтобы компоненты НДСВ были независимы, необходимо и достаточно, чтобы функция распределения компонент Х, У была равна произведению одномерных функций распределения для каждой из компонент. Компоненты Х и У независимы, если вероятность компоненты Х принять какое либо значение не зависит от того, какое значение приняла У и наоборот. Условное мат. ожидание Х – это М(Х) определенное при условии, что У приняла некоторое
значение М(Х/У) Регрессия СВ Х на СВ У – совокупность условных мат. ожиданий Х, определенных для всех значений У.
20. Дать определение ковариации. Формула для вычисления ковариации. Свойства ковариации (без доказательства). Ковариация и независимость случайных величин. Ковариация (корреляционный момент) СВ Х и У называют мат. ожидание произведения их отклонений. Cor(X,Y)=M[(X-M(X))*(Y-M(Y))]
Если cor(X,Y)≠0=> X и Y зависимы; если cor(X,Y)=0≠> X и Y независимы; Свойства: 1). X и Y независимы => cor(X,Y)=0; 2). cor(a+bx,c+dy)=bdcor(x,y); 3). cor(X,Y)=cor(Y,X); 4). Д(Х+У)=Д(Х)+Д(У)+2cor(X,Y), для произвольных СВ Х и У; 5). Абсолютное значение cor(X,Y) не превосходит σхσу (cor(X,Y) ≤ σхσу)
21. Дать определение коэффициента корреляции. Свойства коэффициента корреляции (без доказательства). Коэффициент корреляции и независимость случайных величин. Коэффициент
корреляции
|


|
22. Дать определения законов распределения простейших функций двух дискретных случайных величин X и Y: суммы X+Y, произведения X*Y и квадрата случайной величины. Для независимых ДСВ Х и У сумма X+Y=Z является СВ Z, которая принимает значение Zk=Xi+Yj, а вероятность P(Z+Zk)=P(X=Xi)*P(Y=Yj). Для зависимых - P(Z+Zk)=P(X=Xi, Y=Yj). Произведением двух независимых ДСВ является СВ Z, которая принимает значение Zk=Xi*Yj, P(Z+Zk)=P(X=Xi)*P(Y=Yj). Zk=Xi², P(Z=Zk)=P(X=Xi)
23. Свойства двумерной нормально распределенной случайной величины. Определение распределений Хи-квадрат, Стьюдента и Фишера-Снедекора. Если
ДСВ распределена нормально, то обе
регрессии являются линейными функциями
Ели 2 СВ распределены нормально и их компоненты некоррелируемы cor(X,Y)=0=>X,Y независимы, если X,Y~N Распределением
Хи-квадрат χ² с к степенями свободы
называется распределение суммы
квадратов к независимых СВ каждая из
которых имеет стандартное нормальное
распределение.
Г
–гамма функция Эйгера.
Распределение Стьюдента (Т распределение)
Распределение Фишера-Стьюдента (F распределение). F распределение имеет 2 сиепени свободы к1 и к2
24. Предмет математической статистики. Способы представления данных. Дать определение полигона и гистограммы. Формула Стерджерса для интервальных рядов. МС-это раздел ТВ, который посвящен методу принятия решений в условиях неопределенности. 1) Методы сборки и группировки данных; 2). Методы статистического анализа данных. Гистограмма – графическое представление интервальных рядов. Для полигона берут середины интервалов. Полигон частот – ломаная, отрезки которой соединяют точки (x1,n1), (x2,n2), …,(xk,nk), где xi-варианты выборки, ni – соответствующие им частоты. Формула Стерджерса: k=1+1.4ln n
|
25. Дать определения генеральной совокупности, выборки, вариационного ряда, статистического распределения выборки. Определение репрезентативности выборки. Генеральная совокупность-это множество объектов (наблюдений), которые описывают некоторое явление. Выборка (выборочная совокупность) - случайным образом отобранные из генеральной совокупности объекты. Репрезентативная (представительная) – это выборка, которая правильно представляет свойства и пропорции объектов генеральной совокупности. Вариационный ряд – последовательность вариантов, расположенных в порядке возрастания их числовых значений. Статистическое распределение выборки – перечень вариантов, расположенных в порядке возрастания и соответствующих им частот или относительных частот.
26. Дать определение состоятельности, эффективности и несмещенности точечных оценок параметров генеральной совокупности. Несмещенной называют оценку θ, если её мат ожидание равно истинному значению оцениваемого параметра. Оценка θ называется состоятельной, если она сходится по вероятности к истинному значению оцениваемого параметра. Для всех ε>0 limP(|θ-θ*|<ε)=1 Эффективной называется оценка, которая при заданном объеме выборки имеют наименьшую дисперсию Д(θ) - min.
28. Дать определение доверительного интервала, надежности и погрешности. Построение доверительного интервала для математического ожидания при известной дисперсии. Интервал θ-δ<θ*<θ+δ доверительный, если выполняется условие P(|θ-θ*|<δ)=γ Вероятность γ – надежность (γ=0,9, 0,95, 0,975, 0,99) C вероятностью γ доверительный интервал накроет θ. P(θ1<θ*<θ2)=γ δ-погрешность (ошибка) оценки P(|θ-θ*|<δ)=γ
|






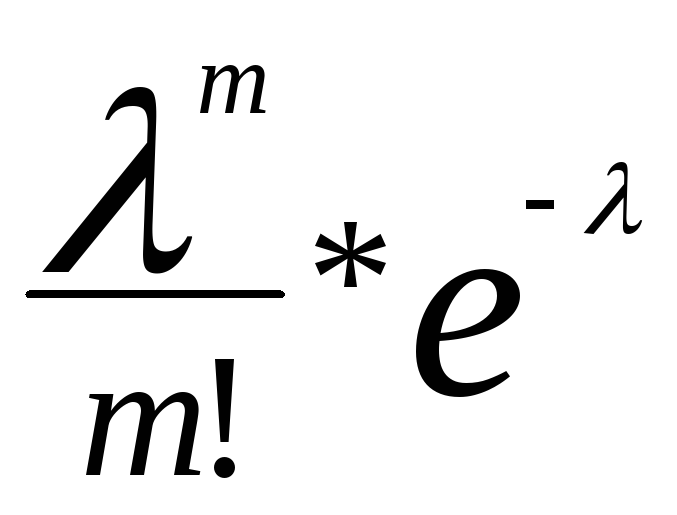
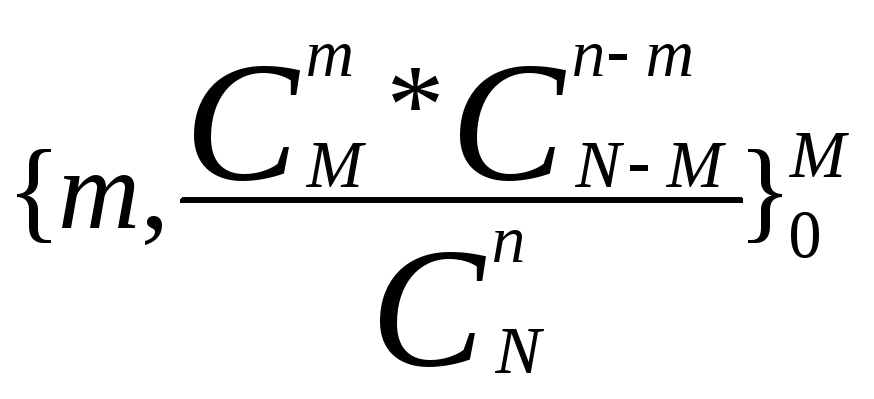 .
.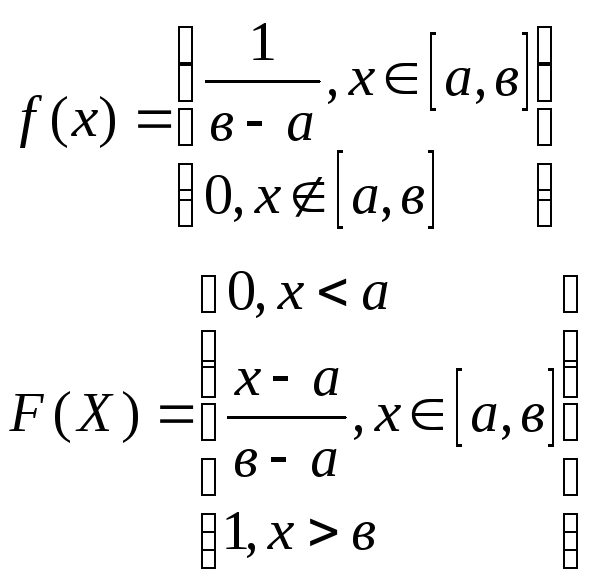
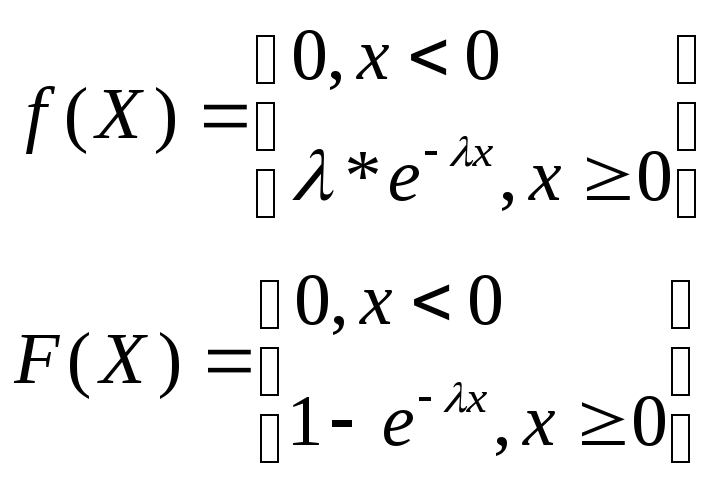
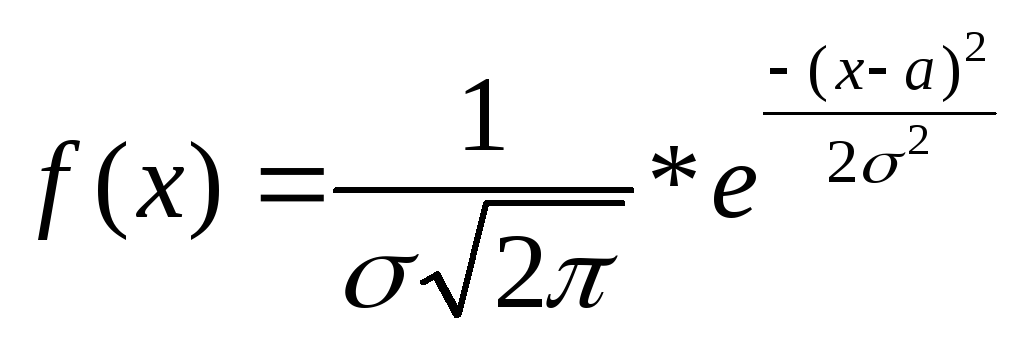

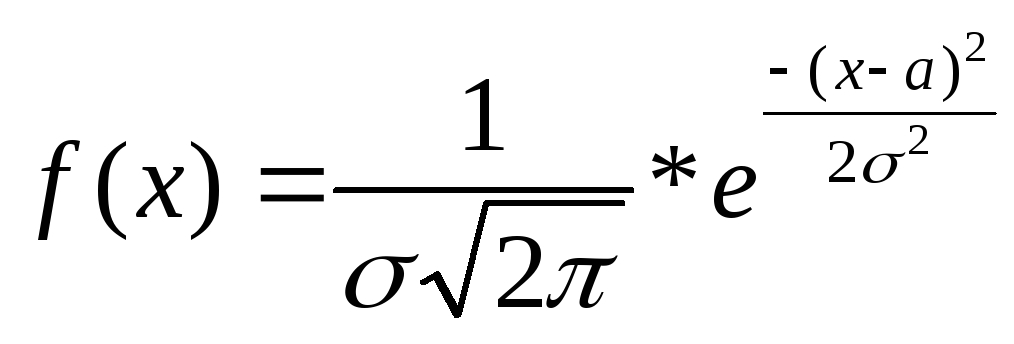
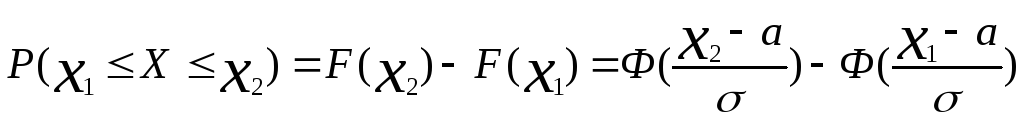
 Эксцесс
Эксцесс
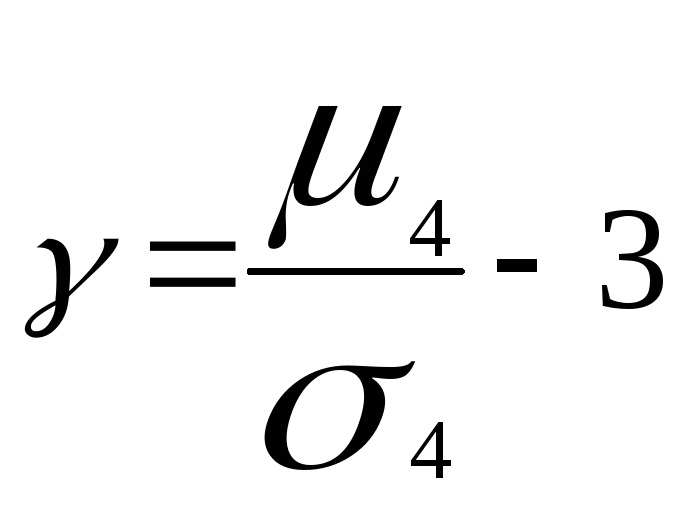

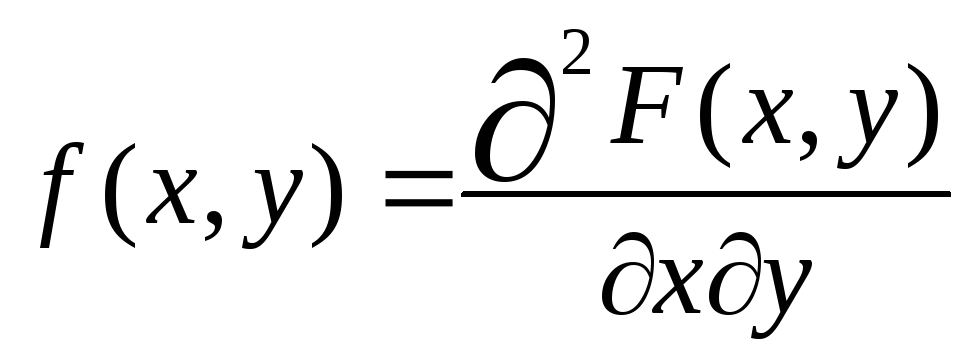
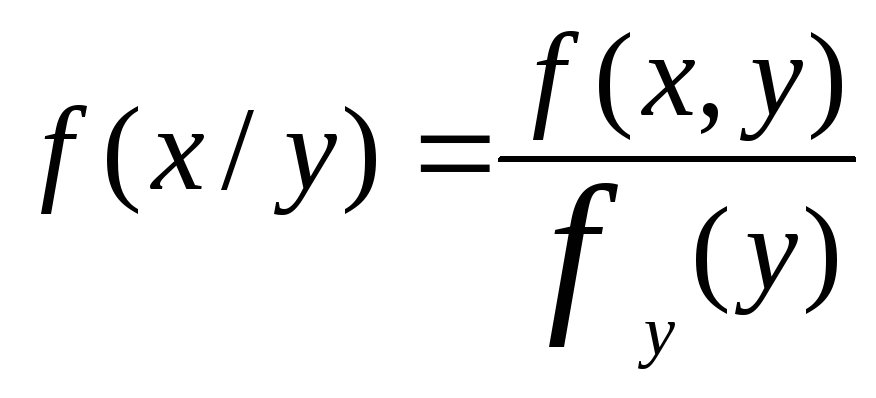
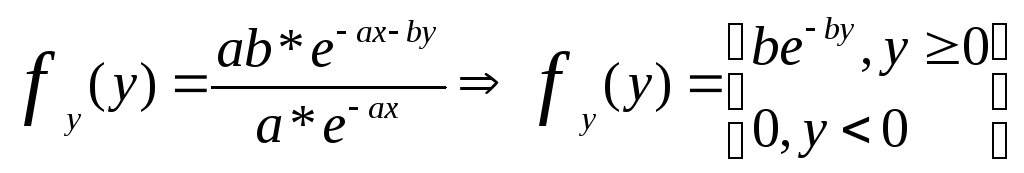


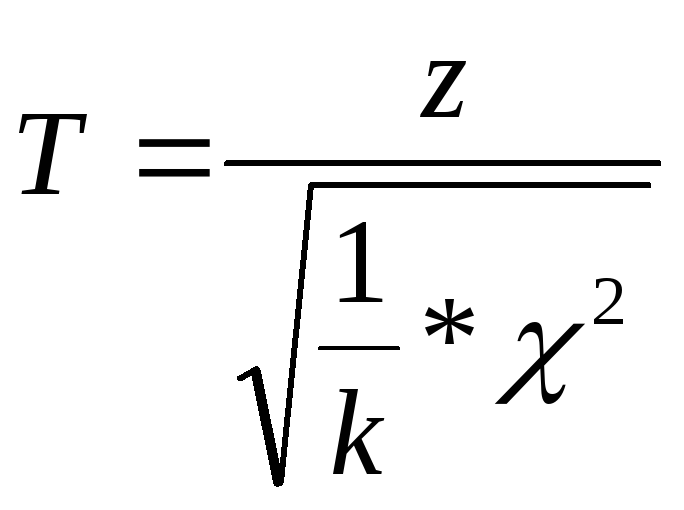
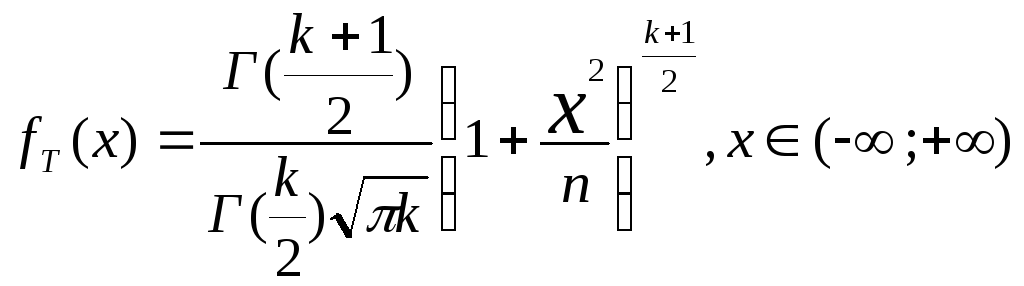 ,
М(Г)=0. Z~N(0,1),
Z
и χ независимы
,
М(Г)=0. Z~N(0,1),
Z
и χ независимы