Вопрос 3 Классическое, статистическое, геометреческое и аксеоматическое определение вероятности события

Классическое: Вероятностью появления события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных и несовместных элемен­тарных исходов.

Статистическое:Статистической вероятностью события А назы­вается относительная частота (частость) этого со­бытия, вычисленная по результатам большого числа испытаний. Будем обозначать ее Р^*(А). Сле­довательно,

Геометрическое:

Если пространство элементарных событий содержит бесконечное множество элементов и ему можно поставить в соответствие некоторое геометрическое пространство, а вероятность каждого события зависит только от меры этого события, а не от его положения, то говорят, что на этом пространстве определена геометрическая вероятность. При этом вероятность каждого события А есть отношение меры А к мере U пространства элементарных событий.

Одним из недостатков классического определения вероятности является то, что оно предпологает конечное число возможных исходов испытаний. Иногда этот недостаток преодолевается использованием геометрического определения вероятност, т.е находят вероятность попадания точки в некоторую область

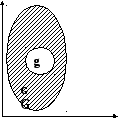
g<G

На G на удачу бросается точка. Событие А состоит в попадании этой точки на фигуру g. Тогда вероятность этого события пропорционально площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g.

Фигуру «g» называют благоприятствоющей событию А, а область применнения геометрической вероятности может быть n-мерной.

Отношение области g к области G. P(A)= (mes g)/(mes G)

Аксиоматическое: Каждому событию А из поля событий сопоставляется неотрицательное число Р(А), называемое вероятностью этого события и удовлетворяющее следующим аксиомам:

1. Р(А) ≥ 0 ; неотрицательность

2. Р(U) = 1, U - достоверное событие ;

3. Р(А+В) = Р(А) + Р(В) , если А и В - несовместны.

Из аксиом о вероятности следует:

1 . Р( V ) = 0 ;

2 . Р(А) = 1 - Р(А) ;

3 . Р(А+В) = Р(А) + Р(В) - Р(АВ) - формула "сложения вероятностей", справедливая для любых событий ;

4 . Если А c В , то Р(В) ≥ Р(А) ;

5 . Если все элементарные события равновероятны и их число конечно и равно n, а событие А включает в себя m элементарных событий, то Р(А) = m/n ;

Вопрос4 Теорема сложения вероятностей несовместных событий. Следствие:Теорема сложения вероятностей совместных событий.

Если события A и B несовместны, то вероятность суммы A+B равна сумме вероятностей этих событий: P(A+B)=P(A)+P(B).

Доказательство: Введем обозначения: n — общее число возможных элементарных исходов испытания; m1 — число исходов, благоприятствующих событию A; m2— число исходов, благоприятствующих событию В.

Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно m1 + m2. Следовательно,

Р (A + В) = (m1 + m2) / n = m1 / n + m2 / n.

Приняв во внимание, что m1 / n = Р (А) и m2 / n = Р (В), окончательно получим

Р (А + В) = Р (А) + Р (В).

Следствие: Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р (A1 + A2 + ... + An) = Р (A1) + Р (A2) + ... + Р (An).

Доказательство: Рассмотрим три события: А, В и С. Так как рассматриваемые события попарно несовместны, то появление одного из трех событий, А, В и С, равносильно наступлению одного из двух событий, A + В и С, поэтому в силу указанной теоремы

Р ( А + В + С) = Р [(А + В) + С] = Р (А + В) + Р (С) = Р (А) + Р (В) + Р (С).

Для произвольного числа попарно несовместных событий доказательство проводится методом математической индукции.