Пуассоновское приближение

Верна следущая предельная теорема:

Теорема Пуассона:

Пусть , таким образом, что, где - заданное число. Тогда для любого фиксированного

.

Другими словами, в описанном предельном переходе биномиальные вероятности аппроксимируются пуассоновским распределением.

Доказательство:

Для краткости будем считать, что , .Тогда

,

поскольку выражение в квадратных скобках стремится к единице, если  фиксировано, а .

Нормальное приближение

Здесь мы рассмотрим случай, когда число испытаний в схеме Бернулли растет , а вероятность успеха в единичном испытании остается фиксированной.

Верна так называемая интегральная теорема Муавра-Лапласа.

Теорема Муавра-Лапласа:

Пусть - число успехов в последовательности из независимых испытаний Бернулли с вероятностью успеха в единичном испытании . Пусть . При

(2),

где .

Замечание 1.

Функция , появившаяся в этой теореме, называется функцией распределения стандартного нормального закона.

Дл язначений этой функции существуют подробные таблицы. Отметим, что она не зависит ни от каких параметров. Следовательно, предел в теореме Муавра-Лапласа является универсальным, так как он не зависит от параметра , который имеется в допредельном выражении. На самом деле, эта теорема является частным случаем другой, еще более универсальной центральной предельной теоремы.

Замечание 2.

Чтобы понять смысл выражения (3),

необходимо вспомнить, что  и . Таким образом, это выражение имеет вид . Легко видеть, что , а .

Преобразование (3) называется центрированием и нормированием случайной величины .

Замечание 3.

В предельном переходе ", " фиксировано"

каждая "индивидуальная" вероятность  стремится к нулю. Асимптотика этого стремления описывается так называемой локальной предельной теоремой. Что же касается интегральной предельной теоремы Муавра-Лапласа, то можно сказать, что она описывает предельное поведение сумм большого числа таких малых вероятностей. Действительно,

,

таким образом, в последней сумме содержится много (порядка ) слагаемых.

Замечание 4.

Скорость сходимости в (2) хорошо изучена. Имеет место так называемая оценка Берри-Эссеена:

Существует такое , что

.

О применимости предельных теорем в схеме Бернулли

Следует различать ситуации, когда к схеме Бернулли можно применить пуассоновскую, а когда нормальную аппроксимации. Из формулировок теорем Пуассона и Муавра-Лапласа, а также Замечания 4 можно вывести следующие общие правила:

1.Если  велико, а  не велико, следует пользоваться пуассоновским приближением;

2.Если  велико и  велико, то можно применять нормальное приближение.

На практике в ситуации, когда  имеет порядок сотен, поступают следующим образом: если , то применяют пуассоновское приближение; если же  имеет порядок нескольких десятков, топользуются нормальной аппроксимацией.

12. Локальная и интегральная теорема Муавра-Лапласа.

Локальная теорема Лапласа

Использование формулы Бернулли при больших значениях  требует выполнения арифметических действий над огромными числами, что обусловлено наличием факториалов в формуле для числа сочетаний. Поэтому, если число испытаний  достаточно велико, то для нахождения вероятности появления события  ровно  раз применяют следующую теорему. Теорема. Если вероятность  появления события  в каждом испытании постоянна и отлична от нуля и единицы, то вероятность  того, что событие  появится в  испытаниях ровно  раз, приближенно равна (тем точнее, чем больше ) значению функции. Для положительных значений аргумента значения функции  приведены в специальной таблице. Для отрицательных значений аргумента пользуются той же таблицей и свойством четности функции , то есть . Таким образом, вероятность того, что событие  появится в  испытаниях ровно  раз, приближенно равна , где .

Интегральная теорема Лапласа

Теорема. Если вероятность  появления события  в каждом испытании постоянна и отлична от нуля и единицы, то вероятность  того, что событие  появится в  испытаниях от  до  раз, приближенно равна определенному интегралу 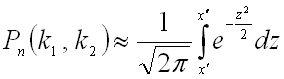, где . При решении задач, требующих применения интегральной теоремы Лапласа, используют специальную таблицу для интеграла . В ней приведены значения функции (которую называют функцией Лапласа) для . Если , то принимают . Для пользуются той же таблицей и свойством нечетности функции Лапласа, то есть . Для того чтобы можно было пользоваться таблицей, преобразуем формулу из интегральной теоремы Лапласа:Таким образом, вероятность того, что событие  появится в  испытаниях от  до  раз, может быть вычислена по формуле   , где .