21. Непрерывная случайная величина. Числовые характеристики непрерывных случайных величин.

Часто приходится иметь дело с такими случайными величинами, возможные значения которых сплошь заполняют некоторый интервал (,); таковы, например, ошибки измерения. Закон распределения такой величины X должен позволять находить вероятность попадания ее значения в любой интервал (x₁,x₂), лежащий внутри (). Будем обозначать эту вероятность через Р(х₁<X< х₂).

Определение 1: Величина X называется непрерывной случайной величиной, если вероятность попадания ее значения в любой интервал (x₁,x₂) может быть представлена в виде интеграла

             (7.6)

от некоторой функции р(х) - плотности распределения вероятностей. При этом функция р(х) должна бытьнеотрицательной (что связано с неотрицательностью вероятностей) и должна быть нормирована условием

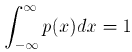(7.7)

отражающим достоверность события (сравни с (1) ). Если все возможные значения случайной величины X сосредоточены в конечном интервале (,), то считается, что вне этого интервала плотность р(х) = 0 и, значит, условие (7.7) сводится к условию

                             (7.8)

Следует подчеркнуть, что для непрерывной случайной величины имеет смысл рассматривать только такое событие, как попадание в интервал, а не попадание в отдельную точку. Так как вероятность попадания непрерывной случайной величины в любую заранее заданную точку равна нулю.

Кривая распределения вероятностей.

Рис. 7.1. Пример кривой распределения вероятностей.

 

Наглядное представление о непрерывном законе распределения вероятностей можно получить по графику плотности распределения р(х), который называется кривой распределения вероятностей величины X (Рис. 7.1). Этот график позволяет иллюстрировать вероятность Р(х₁<X< х₂);-, действительно, площадь, заштрихованная на Рис. 7.1, по свойствам определенного интеграла равна значению  выражения (7.6).

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ

ВЕЛИЧИН

Пусть непрерывная случайная величина Х задана плотностью распреде-

ления f(х). Допустим, что все возможные значения X принадлежат отрезку [а;b]. Разобьем этот отрезок на п частичных отрезков длиной Δx1 , 2 Δx , ..., n Δx и выберем в каждом из них произвольную точку i x ( i=1, 2, ..., п).

Определим математическое ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений i x , на

вероятности попадания их в интервал i Δx :

Перейдя к пределу, получим определенный интеграл

Математическим ожиданием непрерывной случайной величины X,

возможные значения которой принадлежат отрезку [а;b], называют определенный интеграл

Если возможные значения принадлежат всей оси Ох, то

Предполагается, что несобственный интеграл сходится абсолютно, т, е.

существует интеграл

Если бы это требование не выполнялось, то

значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к − ∞ , а верхнего - к + ∞ .

По аналогии с дисперсией дискретной величины определяется и диспер-

сия непрерывной величины.

Дисперсией непрерывной случайной величины называют математиче-

ское ожидание квадрата ее отклонения.

Если возможные значения Х принадлежат отрезку [а;b], то

если же возможные значения распределены по всей оси Ox, то

Среднее квадратическое отклонение непрерывной случайной величины

определяется, как и для величины дискретной, равенством

Замечание 1. Можно доказать, что свойства математического ожидания и

дисперсии дискретных величин сохраняются и для непрерывных величин.

Замечание 2. Легко получить для вычисления дисперсии более удобные

формулы:

Другие числовые характеристики случайных величин

Кроме математического ожидания и дисперсии, на практике часто приме-

няются и другие характеристики положения случайной величины, в частности

мода и медиана.

Модой дискретной случайной величины называется ее наиболее вероятное значение.

Для непрерывной случайной величины мода есть такое значение случай-

ной величины, для которой

На рис.1.11, 1.12 показана мода для дискретной и непрерывной случайной величины.

Если многоугольник распределения (кривая распределения) имеет два

или несколько максимумов, то распределение называется многомодальным

Медианой D M случайной величины X называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины, т.е.

Геометрически медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам (рис.1.17). Каждая из этих

площадей равна 0,5, т.к. вся площадь, ограниченная кривой распределения,

равна 1.

Поэтому

Заметим, что если распределение одномодальное и симметрическое, то

все три характеристики положения случайной величины – математическое

ожидание, мода и медиана – совпадают.