27. Зависимость и независимость двух случайных величин. Числовые характеристики двумерной с.В. Математическое ожидание и дисперсия.
Распределения соответствующих компонент в
одной и другой таблицах одинаковы.
Однако очевидно,
что эти таблицы описывают абсолютно
различные распределения двумерного
случайного вектора 
(все
значения 
в
одной таблице отличны от соответствующих
значений 
в
другой таблице).
Таким образом, на поставленный выше вопрос можно дать следующий ответ: «Зная законы распределения отдельных случайных величин X и Y, входящих в систему, найти закон распределения всей системы в общем случае нельзя».
Заметим, что это можно сделать только в одном частном случае, когда случайные величины X и Y, образующие систему, независимы.
Определение. Две случайные величины X и Y называются независимыми, если независимы все связанные с ними события.
Например, 
и 
; 
и 
и
т.д.
Замечание. Так как зависимость и независимость событий всегда взаимны (если событие A не зависит от события B, то и событие B не зависит от события A), поэтому зависимость и независимость случайных величин также всегда взаимны: если случайная величина X не зависит от случайной величины Y, то Y не зависит от X.
В терминах законов распределения независимость случайных величин можно определить так: «Две случайные величины называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая».
Если
компоненты X и Y двумерного
вектора 
независимы,
то функция распределения 
выражается,
через функции распределения отдельных
компонент:
.
Верно и обратное утверждение. Это правило является необходимым и достаточным условием независимости для случайных величин любого типа.
Необходимые и достаточные условия независимости компонент X и Y для дискретного и непрерывного случаев:
1. X и Y являются независимыми дискретными случайными величинами тогда и только тогда, когда для всех значений индексов i и j выполняется
.
2. X и Y являются независимыми непрерывными случайными величинами тогда и только тогда, когда
.
Отметим,
что допускается нарушение
последнего равенства на множестве
точек 
,
имеющих двумерную площадь, равную нулю.
Ответ: компоненты X и Y независимы.
Замечание. В
данном случае независимость
компонент X и Y можно
было установить, внимательно посмотрев
на исходную таблицу, задающую закон
распределения случайного вектора 
.
Из этой таблицы видно, что закон
распределения каждой из компонент не
зависит от того, какое значение приняла
другая компонента.
Числовые характеристики двумерных случайных величин.
Def:
математическим ожиданием
составляющей 
двумерной
дискретной случайной величины 
называют
число:
Математическим
ожиданием составляющей 
двумерной
дискретной случайной величины 
называют
число:
Def:
математическим ожиданием
составляющей 
непрерывной
двумерной случайной величины 
называют
число:
,
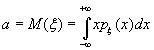где 
В результате получим:
Математическим
ожиданием составляющей 
непрерывной
двумерной случайной величины 
называют
число:
Def:
дисперсией составляющей 
двумерной
дискретной случайной величины называют
число:
Дисперсией
составляющей 
двумерной
дискретной случайной величины называют
число:
Def:
дисперсией составляющей 
двумерной
непрерывной случайной величины 
называют
число:
дисперсией
составляющей 
двумерной
непрерывной случайной величины 
называют
число:
Корни квадратные из дисперсии называют средними квадратичными отклонениями составляющих:
Корреляционный момент (ковариация).