22. Закон равномерного распределения.

Равномерный закон распределения.

На практике встречаются случайные величины, о которых заранее известно, что они могут принять какое-либо значение в строго определенных границах, причем в этих границах все значения случайной величины имеют одинаковую вероятность (обладают одной и той же плотностью вероятностей).

Например, при поломке часов остановившаяся минутная стрелка будет с одинаковой вероятностью (плотностью вероятности) показывать время, прошедшее от начала данного часа до поломки часов. Это время является случайной величиной, принимающей с одинаковой плотностью вероят ности значения, которые не выходят за границы, определенные продолжительностью одного часа. К подобным случайным величинам относится также и погрешность округления. Про такие величины говорят, что они распределены равномерно, т. е. имеют равномерное распределение.

 Определение. Непрерывная случайная величина Х имеет равномерное распределение на отрезке [а, в], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т. е. если дифференциальная функция распределения f(х)имеет следующий вид:

Иногда это распределение называют законом равномерной плотности. Про величину, которая имеет равномерное распределение на некотором отрезке, будем говорить, что она распределена равномерно на этом отрезке.

Найдем значение постоянной с. Так как площадь, ограниченная кривой распределения и осью Ох, равна 1, то

откуда с=1/(b-a).

 Теперь функцию f(x) можно представить в виде

  

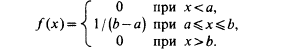
Построим функцию распределения F(x), для чего найдем выражение F(x) на интервале [a, b]:

Графики функций f(x) и F(x) имеют вид:

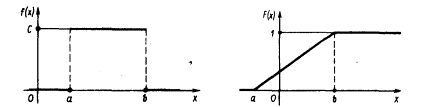
 Найдем числовые характеристики.

Используя формулу для вычисления математического ожидания НСВ, имеем:

Таким образом, математическое ожидание случайной вели чины, равномерно распределенной на отрезке [a, b] совпадает с серединой этого отрезка.

Найдем дисперсию равномерно распределенной случайной величины:

откуда сразу же следует, что среднее квадратическое отклонение:

Найдем теперь вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (,), принадлежащий целиком отрезку [a, b]: 

Геометрически эта вероятность представляет  собой площадь заштрихованного прямоугольника. Числа а и b называютсяпараметрами распределения и однозначно определяют равномерное распределение.

23. Экспонентный закон распределения.

Определение. Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром , если её плотность вероятности f(x) имеет вид:

Кривая распределения  f(x)  приведена на рисунке

Теорема. Функция распределения случайной величины X, распределённой по показательному закону, есть

её математическое ожидание

а её дисперсия

Доказательство.

График функции распределения F(x) случайной величины X, имеющей показательное распределение представлен на рисунке

Следствие. Для случайной величины, распределённой по показательному закону, математическое ожидание равно среднему квадратическому отклонению, т. е.

Показательный закон распределения играет большую роль в теории массового обслуживания и теории надёжности. Так, например, интервал времени Т между двумя соседними событиями в простейшем потоке событий имеет