adapt_curs

52. Найти a, при которых уравнение

(4a+x) arcsin x=0

имеет ровно один корень.

53. Решить неравенство

2 sin2 x 7 sin x+3>0:

54. Для каждого значения параметра a решить уравнение

sin x+cos(a+x)+cos(a x)=2:

55. Найти a, при которых уравнение

tg x+ctg x=8a sin 2x

имеет хотя бы один корень.

56. Найти значения параметра a, для которых уравнение

p

2 sin x a cos x=2

не имеет решений.

57. Найти значения параметра a, для которых уравнение

p

3 sin x+a cos x=2

имеет хотя бы одно решение.

58. Найти значения параметра a, для которых неравенство

12 sin x a cos x62

справедливо для всех значений аргумента.

59. Найти значения параметра a, для которых неравенство

p

a sin x+ 3 cos x< 2

не имеет решений.

60. Найти сумму коэффициентов и свободного члена приведенного квадратного уравнения, корнями которого являются sin и cos , удовлетворяющие соотношению

101

4.cos2 x3 +2 sin3 x3 =1.

5.tg x tg 3x+tg 5x=0.

Решить уравнения, найти корни, расположенные на заданных промежутках, ответ привести в градусах:

6.ctg x+ sin x =2 на (90 ; 180]. p 1+cos x

7.2 sin x2 +1=cos x на [ 90 ; 0 ).

8.2 sin 5x cos 6x+sin x=sin 7x cos 4x на [40 ; 45 ].

9.4 sin x sin 2x sin 3x=sin 4x на (0 ; 30 ).

10.1+tg x =1+sin 2x на ( 90 ; 0 ). 1 tg x

11.Найти наибольший отрицательный корень (в градусах) уравнения

sin2 x 12 sin 2x 2 cos2 x=0:

12. Найти сумму всех корней уравнения ctg 7x ctg 4x=0 на промежутке [0; 2 ]. Решить уравнения, указать количество различных корней, находящихся на за-

данных промежутках:

13.3 sin2(270 +x)=sin2(180 +x)+sin(180 2x) на [ 180 ; 180 ].

p

sin (x 0; 5) 1=x3 +2x2 3x:

на промежутке [0; ].

18. Найти наименьшее натуральное решение неравенства p

19. Решить систему уравнений

81 tg x

<=tg y; 1+tg x

x y = 6 ::

20. Найти a, при которых уравнение

(a 2x) arccos(x 1)=0

имеет ровно один корень.

102

21. Решить уравнение

2arcsin2 x arcsin x 6=0:

22.Найти a, при которых уравнение

tg x+ctg x=6a sin 2x

имеет хотя бы один корень.

23. При каких значениях параметра a уравнение

sin2 4x+(a2 3) sin 4x+a2 4=0

имеет 4 корня, расположенных на отрезке [3 =2; 2 ]?

24. Найти значения параметра a, для которых уравнение

p

sin x+ 3 cos x=a

не имеет решений.

25. Найти значения параметра a, для которых неравенство

12 sin x+cos x>a

справедливо для всех значений аргумента.

8.5. Проверочный тест

1. Сумма корней уравнения

1 sin 5x= cos 32x sin 32x 2 ;

принадлежащих отрезку [180 ; 270 ], равна

1)360 ; 2) 225 ; 3) 630 ; 4) 222 ; 5) 370 :

2.Число целых решений неравенства

p cos x< 0; 5 2;

принадлежащих промежутку 32 ; 32 , равно

1)0; 2) 1; 3) 2; 4) 3; 5) 4:

3.Значение tgxx1 2 , где x1 наибольший, а x2 наименьший из корней уравнения

3 cos2 x sin2 x sin 2x=0;

принадлежащих интервалу ( 90 ; 90 ), равно

1) 15 ; 2) 15 ; 3) 135 ; 4) 135 ; 5) 45 :

103

4. Число корней уравнения

p

x3 2x2 8x= cos (x+1) 1

равно

1)1; 2) 2; 3) 3; 4) 4; 5) 0:

5.Число различных корней уравнения

(1+cos 4x) sin 2x=cos2 2x

на промежутке (30 ; 90 ) равно

1)0; 2) 2; 3) 1; 4) 3; 5) 5:

6.Наименьший корень уравнения

7 sin2 x sin 2x=5 cos2 x;

принадлежащий промежутку ( =2; =2), есть

1) 4 ; 2) arctg 57; 3) 4 ; 4) arctg 57; 5) 0:

7. Число различных корней уравнения

2 cos2 x+3 sin x=0;

принадлежащих интервалу ( 510 ; 30 ), равно

1)4; 2) 3; 3) 2; 4) 1; 5) 6:

8.Найти значения параметра a, для которых уравнение

p

sin x+ 3 cos x=a

не имеет решений.

9. Найти число корней уравнения

p

x3 2x2 8x= cos (x+1) 1:

10. Найти число различных корней уравнения

(1+cos 4x) sin 2x=cos2 2x

на промежутке (30 ; 90 ).

8.6. Ответы

104

42. ( 5 =3; =3); 43. [ =2; 2 =3); 44. (0; ); 45. ( =2; 0)[(0; =3); 46. ( ; 0); 47.

x2( 7 =6+2 n; =6+2 n), n2Z; 54. При 2 k =66a6 =6+2 k и 5 =6+2 k 6a6

a>4; 21. sin 1; 5; 22. a> 13; 23. a= 2; 24. ( 1; 2)[(2; +1); 25. ( 1; p5=2].

9. Преобразование логарифмических и показательных выражений

Логарифмы, десятичные и натуральные логарифмы. Логарифмы произведения, частного, степени и корня. Основное логарифмическое тождество. Переход к новому основанию. Потенцирование. Преобразование показательных выражений. Преобразование смешанных выражений.

9.1. Справочный материал

Свойства степеней.

Для вещественных a>0; x; y

1)a0 =1;

2)a x = a1x ;

3)axay =ax+y;

105

4)ax =ax y;

ay

5)(ax)y =axy;

6)(ab)x =axbx;

1 p

7)an = n a;

p

8) ak = n ak;

n

p

9)a2 =jaj:

Логарифмом числа b (b>0) по основанию a (a>0; a6=1) называется показатель степени, в которую надо возвести число a, чтобы получилось b:

loga b=x () ax =b:

Основное логарифмическое тождество aloga b =b:

9.2. Примеры

Используя свойства (5) и (1) логарифмов, имеем

log3 3 2 = 2 log3 3= 2:

Ответ: 2.

106

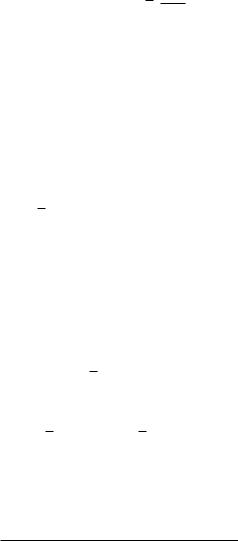
p 3

Пример 2. Найти значение выражения ( 3 7)log2 7 .

Решение. Используя свойство (8) логарифмов, перейдем в показателе степени к логарифму по основанию 7:

37(log2 32+27log3 4)log69 14:

Решение. Используя свойство (5) логарифмов и основное логарифмическое тождество, преобразуем выражение в круглых скобках:

log2 32+27log3 4 =log2(25)+(33)log3 4 =5 log2 2+33 log3 4 = =5+3log3(4)3 =5+43 =69:

Исходное выражение принимает вид 37(69log69 14). Используя основное логарифмическое тождество, окончательно получим

37(69log69 14)= 37 14=6:

Ответ: 6.

Пример 4. Найти значение выражения

3 log23 45 2(log3 45)(log3 5) log23 5: 3 log3 45+log3 5

Решение. Используя свойства (3) и (5) логарифмов, преобразуем числитель дроби

3log23 45 2(log3 45)(log3 5) log23 5=

=3[log3(5 9)]2 2[log3(5 9)](log3 5) log23 5=

=3[log3 5+log3 9]2 2[log3 5+log3 9](log3 5) log23 5=

=3(log3 5+log3 32)2 2(log3 5+log3 32)(log3 5) log23 5=

=3(log3 5+2)2 2 log23 5 4 log3 5 log23 5=8 log3 5+12:

Таким же образом преобразуем знаменатель дроби

3log3 45+log3 5=3 log3(5 9)+log3 5=

=3(log3 5+log3 9)+log3 5=3(log3 5+log3 32)+log3 5=

=3(log3 5+2)+log3 5=3 log3 5+6+log3 5=4 log3 5+6:

107

После упрощения числителя и знаменателя исходное выражение принимает вид

Ответ: 2.

Пример 5. Найти log30 8, если известно, что lg 5=a, lg 3=b. Решение. Представим log30 8 в виде

lg 8 log30 8= lg 30:

Разлагая числа 30 и 8 на простые множители и используя свойства логарифмов,

получаем

3 lg 2 log30 8= lg 5+lg 3+lg 2:

Учитывая, что

lg 2=lg 105 =1 lg 5

и используя условие задачи, получаем

3(1 a) log30 8= b+1 :

Ответ: 3(1 a): b+1

9.3. Аудиторные задачи

1

9.492 log9 7 .

10.2 log3 63 4 log3 7. log81 3 log9 3

108

11.(0; 8)1=(3 log27 4) 51=(3 log27 4).

12.log3[(log2 5)(log5 8)].

13.8log2 p3 p5+3 3log9(p5 3)2 .

p

pp p

15.5logp5 7+ 21+log1=5( 7+ 3).

16.0; 25(1+4log2 5)log26 4.

2log6 18

22.log6 3+ log2 6 .

25.Вычислить logp3 6 0; 6, если log5;4 27=a.

26.Вычислить log1;25 3; 2ma, если logm 5=c, logm 4=a.

Найти значения выражений:

4log4 24

30.(log3 2+log2 81+4)(log3 2 2 log18 2) log2 3 log3 2:

если a2 +b2 =7ab, a>0, b>0.

109

9.4. Домашнее задание

Найти значения выражений:

1. log4 15 +log4 36+ 12 log4 2581.

2. log3 log2 8. p9 2

3. ( 5)log9 5 .

4.103 lg 4 49log7 15.

5.9x +9 x, если 3x +3 x =3.

pp

если известно, что logapb=14.

18.Вычислить logp3 6 2; 7, если log0;1 27=a.

4

19.Найти значение выражения log(8 p4 y) x6 , если a=log2 x и b=logx y.

20.Доказать, что

loga+b m+loga b m=2 loga+b m loga b m;

если известно, что m2 =a2 b2.

110