adapt_curs
.pdf
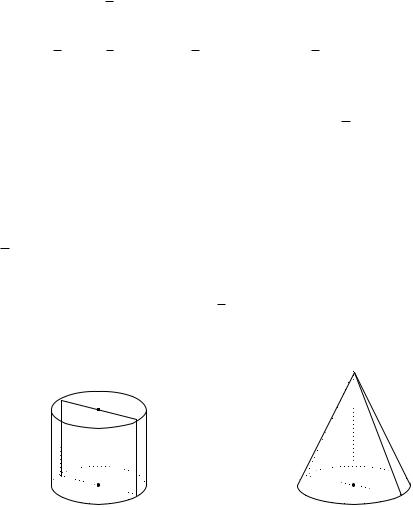
Итак, отрезок DE есть высота нужного нам цилиндра. Найдем его:
p p p
AE = AC2 CE2 = 4r2 r2 = 3r;
и p p p
DE = AE2 AD2 = 3r2 r2 = 2r: p p
Поэтому объем V цилиндра равен V = r2 ( 2r)= r3 2=256 по условию зада-
чи. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
15 |
|
|
||||
|
|
|
|
|
|
|
|
256 |
|
|
|
|
||||||||
|
|
|
3 |
8 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
r |
= |
p |
|
=2 |
2 |
2 =2 |
2 : |
|
|
||||
|
|
|
2 |
|||||||||||||||||
|
5 |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
Тогда r =2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
=4 2, поэтому ребро тетраэдра равно 2r =8 2. |
|||||||||||||||||||
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: 8 |
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 3. Три ребра куба лежат на ребрах тетраэдра ABCD, а вершина P на грани ABC. Найти ребро куба, если DA=2, DB =4, DC =6 (см. рис. 37).
Решение. Из условия задачи и рис. 37 мы видим, что ребра AD, BD, CD взаимно перпендикулярны. Введем прямоугольную систему координат, взяв за начало координат точку D, ось абсцисс направив по прямой DA, ось ординат по прямой DC и ось аппликат по прямой DB.
B




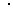 P
P 
 D
D












 C
C
A
Рис. 37.
Тогда координаты точек A; C; B будут такие: A(2; 0; 0), B(0; 0; 4) и C(0; 6; 0). Если ребро куба обозначить через x, то точка P будет иметь координаты P (x; x; x) и лежать на плоскости, проходящей через точки A; B; C:
Соединим точку P с вершинами тетраэдра A; B; C; D, тогда наш тетраэдр разобьется на три пирамиды ADCP , ABDP , BCDP , а ребра куба будут их высотами (см. рис. 38). Эти высоты имеют длину, равную длине ребра куба x.
Найдем объем V первоначального тетраэдра ABCD. Он равен произведению длин ребер AD, DC, BD, деленному на 6 (ребра взаимно перпендикулярны!):
V = 2 4 6 =8: 6
Представим тот же объем в виде суммы объемов треугольных пирамид ADCP , ABDP , BCDP . Эти объемы равны произведению высоты x на площади соответствующих оснований (площади граней ADC, ADB, DBC) (все эти грани являются прямоугольными треугольниками), деленному на 3.
181