adapt_curs

x2y3 =8;

71.x3y2 =4:

x+y +xy =7; 72. x2 +y2 +xy =13:

Решить системы уравнений:

73.

x+y +2xy =7; xy +2(x+y)=8:

y2 xy =12;

74.x2 xy = 3:

Среди решений (x; y) системы найти то, для которого сумма (x+y) максимальна.

не имеет решений?

79. При каких a система

jyj x=1; x2 +y2 =a

имеет ровно два решения?

80. При каких k выполняются неравенства x0 <0, y0 >0, где (x0; y0) решение системы уравнений

51

p p p

x2 +y2 + 2xy =8 2;

84. px+py =4:

4.4. Домашнее задание

pp7 x

9.3+ 3 1 x+2=2.

Решить уравнения с модулем:

10.jx 2j j5+xj=3.

11.x2 +jx 2j 10=0.

12.jx+2j=2x 8.

2 13. jx+2j= 3 x.

14. jx2 +4x+2j= 5x+16. 3

15.jx2 4jxjj=5.

16.Найти сумму корней уравнения j(x 5)3 76j=49.

17.Найти разность между наибольшим и наименьшим корнями уравнения x2 +jxj= 74.

52

p

18.При каких a уравнение 24jxj4x2 =a имеет ровно 3 корня?

19.Найти произведение корней уравнения

x2 +jxj+a=0:

При каких значениях параметра a системы не имеют решений:

25.

4x+ay =1+a;

(6+a)x+2y =3+a:

26.

16x+ay =4; ax+9y 3=0:

При каких a системы имеют бесконечно много корней:

27.

ax (a+1)y =6; 7ax 28y =6(a+4):

28.

x+ay =1;

ax 3ay =2a+3:

29.Найти значение параметра b, при котором прямая y =5x+b проходит через точку пересечения прямых 3x y 3=0 и 2x+3y 13=0.

30.При каких значениях параметров a и b система уравнений

2x ay = 1;

4x+3y =b

имеет бесконечно много корней? Решить системы уравнений:

8

6x+2y z =4;

<

31.4x y +3z = 4;

: 3x+2y 2z =5:

8

2x+y +z =7;

<

32.x+2y +z =8;

: x+y +2z =9:

Среди решений (x; y) системы найти то, для которого сумма (x+y) максимальна. Вычислить значение этой суммы:

x2 +y2 =10;

33.x2y2 =9:

53

px+py =8;

39.x+y px+py 2pxy =2:

40.При каких k система уравнений

x+ky =2k +1;

2jx 1j=y 2

имеет бесконечно много решений? 41. При каких a система уравнений

jxj+jyj=1; y =a x

имеет больше двух решений?

4.5. Проверочный тест

1. Значение x3 +10x, где x корень уравнения

pp

6 x 2x 3=0;

равно

1) 57; 2) 57; 3) 75; 4) 72; 5) 72:

3.Уравнение jx+4j+jx 10j=a не имеет корней, если

1)a>14; 2) 0<a614; 3) a<14; 4) a=6; 5) a<5:

4.Уравнение

p

6jxj x2 =a

имеет ровно два корня при a равном

1) 3; 2) 2; 3) 4; 4) 1; 5) 0:

54

решения, при a=4 три решения, при a>4 два решения; 49. При a=1 x>1; при

7+a

a= 1 36x61, при jaj<1 x=1, x= a 1, т. е. два решения; при jaj>1 x=1, т. е. одно решение; 50. 63; 51. (2, 3); 52. (4, 3); 53. (1,2; 0,7); 54. (26,5; -5,5); 55. a=0;

56. a= 12; 57. a= 1; 58. a=1; 59. a=3; 60. a=2; 61. 43; 62. (2, 3, 1); 63. (1, 2,

5. Рациональные неравенства

Числовые неравенства, их свойства. Неравенства с одной переменной, равносильные преобразования неравенств. Решение квадратных неравенств, рациональных неравенств. Метод интервалов. Системы рациональных неравенств. Равносильные преобразования систем. Совокупность систем неравенств. Неравенства с параметром.

5.1. Справочный материал

Пусть даны две функции y =f(x) и y =g(x). Выражения вида

f(x)>g(x); f(x)<g(x); f(x)>g(x); f(x)6g(x)

называются неравенствами с одним неизвестным.

Областью допустимых значений (ОДЗ) неравенства f(x)>g(x) (f(x)<g(x), f(x)>g(x), f(x)6g(x)) называется общая часть (пересечение) областей существования функций y =f(x) и y =g(x), т. е. множество всех числовых значений неизвестного x, при каждом из которых имеют смысл (определены) левая и правая части неравенства.

Любое число x из ОДЗ неравенства называется допустимым значением для данного неравенства.

Число из ОДЗ неравенства называется решением неравенства, если при подстановке его вместо неизвестного в неравенство оно превращается в верное числовое неравенство.

56

Решить неравенство это значит найти множество всех его решений. Нахождение ОДЗ позволяет в некоторых случаях доказать, что неравенство не

имеет решений и часто дает возможность упрощать процесс решения неравенства. p p p

Так, например, ОДЗ неравенства x 8+ 4 x> x есть пустое множество. p

Решениями неравенства x2 +5x+6> 2 являются все x из его ОДЗ.

Пусть даны два неравенства. Если любое решение первого неравенства является решением второго неравенства, а любое решение второго неравенства решение

первого, то такие неравенства называются равносильными. p

Например, неравенства x2 >0 и x4 >0 равносильны, а неравенства x>1 и x2 >1 равносильными не являются.

Пусть даны два неравенства и некоторое множество M. Если любое решение первого неравенства, принадлежащее множеству M, является решением второго неравенства, а любое решение второго неравенства, принадлежащее M решение первого, то такие два неравенства называются равносильными на множестве M.

не являются равносильными на множестве всех действительных чисел, но равносильны, например, на промежутке 1<x<0.

Утверждения о равносильности неравенств:

1.Неравенства f(x)>g(x) и f(x) g(x)>0 равносильны.

2.Неравенства f(x)>g(x) и f(x)+ >g(x)+ равносильны для любого числа .

3.Неравенства f(x)>g(x) и f(x)> g(x) равносильны для любого положительного числа .

4.Неравенства f(x)>g(x) и f(x)< g(x) равносильны для любого отрицательного числа .

5. Если функции y ='(x) и y =g(x) тождественно равны, то неравенства f(x)>g(x) и f(x)>'(x) равносильны.

6. Пусть n натуральное число и на некотором множестве M функции y =f(x) и y =g(x) неотрицательны. Тогда на этом множестве неравенства f(x)>g(x) и

(f(x))n >(g(x))n равносильны.

7. Пусть на множестве M, содержащемся в ОДЗ неравенства f(x)>g(x), функция y ='(x) положительна. Тогда на этом множестве равносильны неравенства

f(x)>g(x) и f(x)'(x)>g(x)'(x):

8. Пусть на множестве M, содержащемся в ОДЗ неравенства f(x)>g(x), функция y ='(x) отрицательна. Тогда на этом множестве равносильны неравенства

f(x)>g(x) и f(x)'(x)<g(x)'(x):

9. Если функции y ='(x) и y =g(x) тождественно равны на множестве M, то неравенства f(x)+'(x)>0 и f(x)+g(x)>0 равносильны на множестве M.

Рассмотрим m неравенств f1(x)>g1(x); : : : ; fm(x)>gm(x). Обозначим через Q область, являющуюся пересечением областей допустимых значений этих неравенств.

57

Если нужно найти все числа из области Q, каждое из которых решение каждого из этих неравенств, то говорят, что дана система m неравенств

8

>f1(x)>g1(x)

<

. . . . . . . . . . . . . .

>

:fm(x)>gm(x);

и область Q называют областью допустимых значений (ОДЗ) этой системы. Числоиз ОДЗ системы называется решением данной системы, если оно является решением каждого из неравенств системы. Решить систему неравенств значит найти множество всех ее решений. Если это множество окажется пустым, то говорят, что система неравенств не имеет решений.

Систему неравенств обычно решают следующим образом: сначала решают каждое неравенство на ОДЗ этой системы, затем находят множество, являющееся пересечением всех этих множеств решений.

Говорят, что неравенство f(x)>g(x) равносильно совокупности систем неравенств, если множество его решений совпадает с множеством решений данной совокупности.

Замена неравенства f(x)>g(x) равносильной ему совокупностью систем неравенств называется равносильным переходом от неравенства к совокупности систем неравенств.

Рациональные неравенства

Рациональные неравенства это неравенства вида Pn(x)>0 (Pn(x)<0), Pn(x) >0

Qm(x)

Pn(x)

Qm(x)

<0 , где Pn(x); Qm(x) многочлены соответственно степеней n и m, т. е.

Pn(x)=anxn +an 1xn 1 +:::+a1x+a0;

Qm(x)=bmxm +bm 1xm 1 +:::+b1x+b0:

Pn(x) Qm(x)>0 (Pn(x)Qm(x)<0).

Метод интервалов

Рассмотрим неравенство

Pn(x)>0:

Разложим многочлен Pn(x) на множители:

Pn(x)=(x x1)k1 (x x2)k2 (x xl)klQ(x);

где k1, k2,...,kl некоторые натуральные числа, а x1, x2,..., xl различные корни уравнения Pn(x)=0, а многочлен Q(x) не имеет действительных корней. Тогда этот

58

многочлен либо положителен на всей числовой прямой, либо отрицателен на всей числовой прямой. Положим (для определенности) Q(x)>0. Тогда в рассматриваемом неравенстве на него можно сократить. Будем считать также, что

При x>xl все сомножители положительны, поэтому и Pn(x)>0. Если число kl нечетное, то при x2(xl 1; xl) все сомножители в (1) положительны, за исключением последнего, который отрицателен и поэтому на данном промежутке Pn(x)<0. В этом случае говорят, многочлен Pn(x) меняет знак при переходе через корень xl. Если же kl четное, то все сомножители в (1) на промежутке (xl 1; xl) остаются положительными. Следовательно, Pn(x)>0 при x2(xl 1; xl). В этом случае говорят, что многочлен Pn(x) не меняет знака при переходе через корень xl.

Аналогично рассматриваются все остальные корни. Таким образом на каждом из интервалов (на которые разбивается числовая ось точками x1; : : : ; xl) многочлен Pn(x) сохраняет определенный знак. И таким образом, решением неравенства (1) служит объединение тех интервалов из этого разбиения, на котором многочлен Pn(x)положителен.

Итак для нахождения решения неравенства Pn(x)>0 нужно знать все действительные корни многочлена x1; : : : ; xl и степени k1; : : : ; kl.

Аналогично решается неравенство Pn(x)<0. Множеством решений нестрогого неравенства

Pn(x)>0 (Pn(x)60)

является объединение двух множеств: множества решений строгого неравенства Pn(x)>0 (Pn(x)<0) и множества решений уравнения Pn(x)=0.

При решении рационального нестрогого неравенства нужно обязательно учитывать ОДЗ. То есть корни знаменателя мы должны исключить из рассмотрения как при решении строгого неравенства, так и при решении нестрогого неравенства. Сле-

довательно, неравенства Pn(x) >0 и Pn(x) Qm(x)>0 неравносильны.

Qm(x)

5.2. Примеры

Пример 1. Решить систему неравенств

x2 69; x>0:

Решение. Решаем сначала первое неравенство x2 69:

x2 960; (x 3)(x+3)60:

Его решение: 36x63 (рис. 3).

59

Рис. 3

Решение второго неравенства очевидно.

Изобразим на числовой прямой множество чисел, удовлетворяющих первому и второму неравенствам (рис. 4), откуда следует, что оба неравенства верны при 0< x63.

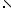
3 0 3 x

Рис. 4

Ответ: x2(0; 3]:

Пример 2. Решить двойное неравенство

1<x2 +x<0:

Решение. Решить двойное неравенство это значит решить соответствующую систему неравенств

1<x2 +x; x2 +x<0:

1)Решим первое неравенство x2 x 1<0. Многочлен, стоящий в левой части неравенства, нельзя разложить на множители, так как уравнение x2 x 1=0 не имеет корней (D = 3<0). Поэтому квадратный трехчлен ( x2 x 1) при всех значениях x имеет постоянный знак, а именно отрицательный (по знаку первого коэффициента). Таким образом, решение этого квадратного неравенства есть промежуток

(1; +1).

2)Решим второе неравенство x(x+1)<0 (рис. 5), его решение интервал x( 1; 0).

3) Найдем пересечение полученных множеств.

Ответ: ( 1; 0).

Пример 3. Решить неравенство (x 2)2(x 3) >0. x+1

Решение. Находим точки, в которых обращается в нуль числитель и знаменатель: x1 = 1, x2 =2, x3 =3. Так как неравенство нестрогое, то x2 =2 и x3 =3 являются решениями неравенства. На числовой прямой отметим точки x1 = 1, x2 =2, x3 =3, причем x2 и x3 обычно изображают как жирную точку , а x1 как "пустую"точку (рис. 6).

60