adapt_curs

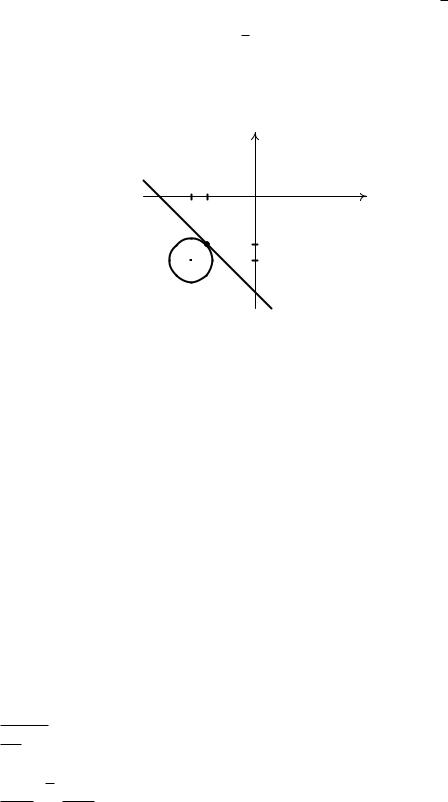
т. е. x+y > 6. Это неравенство задает полуплоскость, расположенную выше прямой, проходящей через точки ( 6; 0) и (0; 6). Преобразуем второе неравенство:

p

(x2 +8x+16)+(y2 +8y +16)62; (x+4)2 +(y +4)2 6( 2)2:

p

Это неравенство задает круг радиуса 2 с центром в точке ( 4; 4). Решением системы неравенств являются общие точки построенной полуплоскости и круга (см. рис. 10). Такая точка только одна, она имеет координаты ( 3; 3).

Ответ: ( 3; 3).

Рис. 10

6.3. Аудиторные задачи

Решить неравенства:

1.j2x 1j jx 2j>4.

2.jx2 11j<10.

Решить неравенства и указать наименьшее целое положительное решение для каждого из них:

3.jx 3j< 1.

4.jx 2j(x 1)>0.

5.j2x2 9x+15j>11.

6.x2 j5x+6j>0.

7.j2x 1j+jx 3j64.

8.jx3 1j(x 9)<0.

9.Найти сумму целых решений неравенства 7+j3x 5j611.

10.Найти сумму целых решений системы неравенств

jxj>5

jx+3j<6:

Решить неравенства: p

11.p9x 20<x.

12.x (x+1)>0.

Решить неравенства и указать их наименьшие целые решения:

13.(x 1)px<0. p p

14.5 x> x+1.

71

x+6 2

Найти число целых решений неравенств:

r

25.12 3x2 63. p x p

26.x 6 x 10>1.

Найти площадь фигуры, заданной неравенствами:

29.jxj+jy 1j64.

30.jx 1j+jy 2j610.

31.x2 +y2 64jxj+6jyj.

32.Найти площадь фигуры, заданной системой неравенств

x64 2jy 1j x>4jy 1j 8:

33. Найти все значения параметра a, при которых неравенство x2 +3jx aj>a2

справедливо для всех x.

34.Решить неравенство jx2 2j+x<0.

35.Найти все значения параметра a, при каждом из которых неравенство

3 jx aj>x2

имеет хотя бы одно отрицательное решение.

6.4. Домашнее задание

Решить неравенства и указать наименьшее положительное целое решение каждого из них:

72

11

1.jxj > 3.

2.jx 2j+jx+2j64.

2 8

3.> .

x 13 9

4.Решить неравенство jx2 7j<6.

5.Найти сумму целых решений неравенства j2x 4j 367.

6.Найти количество целых решений неравенства (x2 2x 3)jx 2j<0.

7.Найти сумму целых решений системы неравенств

jx 6j>3 1<x<10:

Найти длины промежутков, на которых выполняются неравенства:

Найти площадь фигуры, заданной неравенствами:

15.jx+1j+jy 2j65.

16.x2 +y2 64jxj+10jyj.

17.Найти площадь фигуры, заданной системой неравенств

x+2jy +3j66 3x+2jy +3j>6:

Решить неравенства:

6.5. Проверочный тест

jx 1j+jy 3j66;

равна

1) 72; 2) 18; 3) 36; 4) 30; 5) 25:

73

3. Число целых решений неравенства

r

x2 3 <1 x

равно

1)0; 2) 1; 3) 2; 4) 3; 5) 4:

4.Решение неравенства

1+jx 1j >2

2 имеет вид 1) [2; 4]; 2) (1; 2][[4; +1); 3) [2; 4];

4)(1; 2][[4; +1); 5) (2; 4):

5.Сумма целых решений неравенства

j2x 1j+j3 xj64

равна

6x 17>4 x

составляют множество

1)( 3; 3); 2) (1; 0)[[176 ; +1); 3) [176 ; +1); 4) [3; +1); 5) [4; +1):

7.Наибольшее целое решение неравенства

pp

x2 6> x

равно

1)3; 2) 8; 3) 3; 4) 2; 5) 9:

8.Решить неравенство px 1 px+px 1<0; 1.

9.Найти значения параметра a, при которых неравенство

10. Найти наименьшее значение параметра a, при котором множество решений нера-

содержит ровно два целых числа.

74

6.6. Ответы

7. 1; 8. 2; 9. 6; 10. 26; 11. [20=9; 4) [(5; +1); 38. ( 1; 0); 13. Нет целых решений;

14. 1; 15. 0; 16. (3; +1); 17. [ 7; 2); 18. (1; 1][f2g; 19. [ 1; +1); 20. 1; 21.4; 22. 1; 23. 0; 24. 5; 25. 5; 26. 3; 27. 4; 28. 9; 29. 32; 30. 200; 31. 48+26 ; 32.

24; 33. [ 3=2; 3=2]; 34. ( 2; 1); 35. a2( 13=4; 3). Указание: записав неравенство в виде 3 x2 >jx aj, построить и исследовать графики функций, входящих в левую и

[ 5; 1)[(1; +1); 20. [1; +1).

7. Преобразование тригонометрических выражений

Понятие угла и дуги, их градусная и радианная меры. Определение тригонометрических функций числового аргумента: синуса, косинуса, тангенса и котангенса. Промежутки сохранения знака для тригонометрических функций. Вычисление значений тригонометрических выражений без таблиц. Зависимость между тригонометрическими функциями одного аргумента. Основное тригонометрическое тождество. Четность, нечетность. Периодичность. Формулы сложения. Формулы приведения. Тригонометрические функции двойного и половинного аргумента. Преобразование суммы и разности тригонометрических функций в произведение и обратно. Определение обратных тригонометрических функций: арксинуса, арккосинуса, арктангенса, арккотангенса. Нахождение тригонометрических функций от обратных тригонометрических функций.

7.1. Справочный материал

Числовая окружность (тригонометрический круг)

Введем понятие числовой окружности (тригонометрического круга) (рис. 11). Пусть на плоскости задана декартова система координат. Построим окружность радиуса 1 с центром в начале координат.

Поставим в соответствие каждому действительному числу t точку M(t) окружности по следующему правилу:

если t=0, то ему соответствует точка A=M(0) правая точка пересечения окружности с осью Ox;

если t>0, то, отправляясь из точки A, пройдем по окружности против часовой стрелки путь длиной t; конец этого пути и будет искомой точкой M(t);

если t<0, то, отправляясь из точки A, опишем по окружности в направлении по часовой стрелке путь длиной jtj; конец этого пути и будет искомой точкой M(t).

75

M(t)

t

1

OA

Рис. 11. Числовая окружность (тригонометрический круг)

Единичная окружность с установленным соответствием называется числовой или

тригонометрической окружностью.

Из определения понятно, что каждому действительному числу t соответствует единственная точка M(t) числовой окружности и угол между осью x и радиусомвектором точки.

Если точка M соответствует числу t, то она соответствует любому числу вида x=t+2 k, где 2 длина единичной окружности, а k целое число, показывающее количество полных обходов окружности в ту или иную сторону при построении точки

M(t).

Радианная и градусная меры углов

Если величина угла выражена в градусах, то для вычисления ее в радианах следует пользоваться формулой

радиан= 0 :

1800

Отсюда можно получить формулу

0 = радиан 1800:

Градусную меру угла = 24 вычисляют так:

76

Определение тригонометрических функций

Определим основные тригонометрические функции. Пусть задана числовая окружность, t произвольное действительное число и M(t) соответствующая ему точка числовой окружности. Тогда

sin t ордината точки M(t);

Период тригонометрических функций

Напомним, что периодом функций y =sin x и y =cos x является число T =2 . Периодом функций y =tg x и y =ctg x выступает число T = .

Следует помнить, что 2 на самом деле будет наименьшим положительным периодом этих функций. А числа 2 n, где n2Z, также являются периодами функций sin x и cos x.

Известно, что периоды функций

y =A sin (!x+') и y =A cos (!x+')

вычисляются по формуле T = 2! , а период функции

y =A tg (!x+')

по формуле T = ! .

Если период функции y =f(x) равен T1, а период функции y =g(x) равен T2, то период функций y =f(x)+g(x) и y =f(x) g(x) равен наименьшему числу, при делении которого на T1 и T2 получаются целые числа.

Значения тригонометрических функций основных углов

77

Формулы приведения

Обратные тригонометрические функции

Определение 1. =arcsin a, если

1) sin =a; 2) 2[ =2; =2]:

Например, arcsin 0=0, arcsin 1==2, arcsin ( 1)= =2,

Определение 2. =arccos a, если

Например, arccos 0==2, arccos 1=0, arccos ( 1)= ,

Определение 3. =arctg a, если

1) tg =a; 2) 2( =2; =2):

Например, arctg 0=0, arctg 1==4, arctg ( 1)= =4.

Определение 4. =arcctg a; если

Например, arcctg 0==2, arcctg 1==4, arcctg( 1)=3=4.

78

Соотношения между тригонометрическими функциями одного и того же аргумента

sin 2 =2 sin cos ;

cos 2 =cos2 sin2 =2 cos2 1=1 2 sin2 ;

2 tg tg 2 = 1 tg2 ;

sin 3 =3 sin 4 sin3 ; cos 3 =4 cos3 3 cos :

Формулы преобразования сумм или разностей в произведения

79

Преобразование произведений в суммы или разности

sin sin = 12[cos ( ) cos ( + )]; cos cos = 12[cos ( )+cos ( + )]; sin cos = 12[sin ( )+sin ( + )]:

Выражение тригонометрических функций через тангенс половинного аргумента

7.2. Примеры

80