adapt_curs

m (если m>1, то график растягивается в m раз, а если 0<m<1, то график сжимается в m1 раз). Если m<0, то нужно сначала построить график функции y =jmjf(x), а затем отразить его симметрично относительно оси OX.

График функции y =mf(kx + a) + b строят, применяя в определенной последовательности описанные выше преобразования. Сначала строим график функции y =f(x+a). Затем строим график функции y =f(kx+a). Далее строим график функции y =mf(kx+a). Наконец, строим график функции y =mf(kx+a)+b.

Приведем правила построения графиков функций, содержащих знак модуля.

8.Чтобы построить график функции y =jf(x)j из графика функции y =f(x), нужно ту часть графика функции y =f(x), которая находится ниже оси OX, отразить симметрично относительно этой оси; а часть графика функции y =f(x), которая находится выше оси OX, оставить без изменения.

9.Чтобы построить график функции y =f(jxj) из графика функции y =f(x), нужно часть графика функции y =f(x), лежащую правее оси OY оставить без изменения,

авместо оставшейся части графика нарисовать кривую, получающуюся отражением первой части графика функции y =f(x) относительно оси OY .

10.Чтобы построить график функции y =jf(jxj)j из графика функции y =f(x), нужно сначала построить график функции y =f(jxj) согласно второму правилу, а затем из полученного графика построить график функции y =jf(jxj)j согласно первому правилу.

Обратная функция

Пусть D(f) и E(f) соответственно область определения и множество значений функции y =f(x).

Если для любого y из множества E(f) существует единственное число x=g(y) из D(f), то функция y =f(x) называется обратимой. Функция x=g(y) называется обратной функцией (при этом первоначальная функция y =f(x) называется прямой функцией).

Областью определения обратной функции является множество значений прямой функции, а множеством значений обратной функции является область определения прямой функции.

Если для обратной функции использовать стандартные обозначения аргумента и функции y =g(x), тогда графики взаимно-обратных функций y =f(x) и y =g(x) будут симметричны относительно прямой y =x (биссектрисы первого координатного угла).

Для того, чтобы для функции y =f(x) найти обратную функцию, нужно:

1. Решить уравнение y =f(x) относительно переменной x. Если это удалось, то мы получаем соотношение x=g(y), в котором меняем местами x и y;

2. Функция y =g(x) и есть обратная к функции y =f(x);

3. Если уравнение y =f(x) имеет для данного y не одно, а несколько решений, тогда у заданной функции обратной функции не существует. В этом случае нужно пробовать найти обратную функцию не на всей области определения, а на ее части.

Так, например, для функции x2 уравнение y =x2 имеет два решения x= py при y >0. Если взять арифметическое значение корня py, то функция y =px будет обратной к функции y =x2 не на всей области определения, а только при x>0.

131

Отсюда

x= 11+yy :

Переобозначая переменные, получим, что обратная функция имеет вид

y = 1 x

1+x

и, следовательно, совпадает с первоначальной функцией.

Ответ: y = 11+xx.

Пример 4. Построить график функции

y =jx2 +jxj 1j=jjxj2 +jxj 1j:

Сначала строим график функции y =x2+x 1 (параболу). Она обозначена на рис. 14 пунктиром. А затем производим действия согласно первому и второму правилам.

y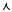

y =jx2 +jxj 1j

1

O 1 x y =x2 +x 1

Рис. 14

Пример 5. При каких значениях параметра a уравнение

jx2 6jxj+5j=a

имеет 8 различных корней?

133

Решение. Строим график функции y =jx2 6jxj+5j=jjxj2 6jxj+5j согласно правилам построения графиков с модулями из графика функции y =x2 6x+5 (рис. 15). Вершина этой параболы имеет координаты (3; 4).

Для того, чтобы прямая y =a пересекала график функции y =jx2 6jxj+5j в восьми точках, необходимо, чтобы a2(0; 4).

Ответ: a2(0; 4).

12.3. Аудиторные задачи

5.y =arccos(0; 5x 1). p

6.y = arcsin x arccos x.

7.y =tg(2 arccos x).

16.Найти функцию g(x), если f(x+2)= x+1 и f(g(x))=4x+5.

17.Функция y =f(x) определена на множестве всех действительных чисел и является периодической с периодом 5. Найдите значение выражения 2f( 6) f(9) f( 8), если f( 1)= 2 и f(2)=3; 5.

18.Функция y =f(x) определена на всей числовой прямой и является четной периодической функцией с периодом 6. На отрезке [0; 3] функция задана формулой f(x)=2+2x x2. Определите количество нулей этой функции на отрезке [ 5; 4].

19.Найти f x1 +f 25x , если f(x)= 75xx+11.

20.Для всех x6= 1 функция f(x) удовлетворяет соотношению

1

(2x 8)f(x+1)+(10 x)f x+1 =4+2x:

134

Найти значение f(x) в точке x0 =3. Найти функции, обратные заданным:

x+1

21. y = x 1.

1

22. y = x3 .

23. y =31 x.

24. y =2x 1 2 x.

25. Графики функций y =f(x) и y =g(x) симметричны относительно прямой y = x. Найти g(x), если f(x)=0; 5x 2.

26. Графики функций y =f(x) и y =g(x) симметричны относительно прямой y = x. Найти g(x), если f(x)=2x 1.

27. Какие из графиков функций y1 =x 1, y2 =p(x 1)2, y3 = px 1 2 совпадают? 28. Найти множество значений параметра a, при которых уравнение

jx2 4jxj+3j=a

имеет ровно 8 корней.

29. Сколько корней имеет уравнение

jx2 2jxj8j=a

при различных значениях параметра a.

30. Пусть

f(x)= x+x 2:

Найти f(f(x)).

12.4. Домашнее задание

f(1=x)=x2 +1; x6=0:

135

10.Найти функцию g(x), если f(x 5)=4x 4 и f(g(x))=4x+8.

11.Для всех x6= 3 функция f(x) удовлетворяет соотношению

1

(7x 2)f(x+3)+(3x 2)f x+3 = 10x+4:

Найти значение f(x) в точке x0 =1.

12.Найти f(x 4) f(x 12), если f(x)= 3x+4. x+8

12.5. Проверочный тест

1. Область значений функции

y =101 2 cos x

есть множество

1) [0; 1000]; 2) [0; 1; 1000]; 3) (0; 1000); 4) [1000; +1); 5) (0; 1; +1):

2.Какое из этих чисел входит во множество значений функции y =3x +7

1)7; 2) 8; 3) 6; 4) 5; 5) 4 ?

3.Область определения функции

p

2x 1

y = 4x2 12x+9

есть множество

1)[ 0; 5; +1); 2) (0; 5; 1; 5]; 3) [0; 5; 1; 5)[(1; 5; +1);

4)( 1; 0; 5)[(1; 5; +1); 5) (1; 5; +1):

4.Графики функций y =f(x) и y =g(x) симметричны относительно прямой y = x. Если f(x)=0; 5x+2, то g(x) равно

1)log2( 4x); 2) log2( 4x); 3) log2(4x); 4) log2(4x); 5) log2(4=x):

5.Уравнение jx2 4jxj+3j=a имеет ровно 4 корня при значениях a, принадлежащих множеству

1)(2; 5)[f0g; 2) (2; 4)[f0g; 3) (1; 3)[f0g; 4) (1; 4)[f0g; 5) (1; 5)[f0g:

136

7. Функция y =f(x) определена на множестве всех действительных чисел и является периодической с периодом 5. Значение выражения f(3) 2f( 7) f(9), если f( 2)=

12.6. Ответы

функций различны; 28. (0; 1); 29. При a2(1; 0) нет корней, при a2f0g[(9; +1)

совпадают; 18. (4; 5)[f0g.

137

13. Исследование функций

Уравнение касательной к графику функции.

Правила вычисления производных: производные суммы, разности, произведения и частного двух функций. Таблица производных. Производная сложной функции. Максимумы и минимумы (экстремумы) функции, промежутки возрастания и убывания. Общая схема построения графиков функций. Нахождение наибольшего и наименьшего значений функции на отрезке. Применение производной для решения задач.

13.1. Справочный материал

Операцию взятия производной называют дифференцированием. Функцию, у которой существует производная в точке x0, называют дифференцируемой в точке x0.

Производные элементарных функций

(C)0 =0; (kx+b)0 =k;

(x )0 = x 1; 2R; (ex)0 =ex;

(arcctg x)0 = 1+1x2 :

138

Правила дифференцирования

Пусть C постоянная; u; v дифференцируемые функции. Тогда

(Cu)0 =Cu0; (u+v)0 =u0 +v0; (uv)0 =u0v +uv0;

где '(f(x)) сложная функция.

Уравнение касательной к графику функции y =f(x) имеет вид y y0 =f0(x0)(x x0); y0 =f(x0);

где (x0; y0) точка касания; f0(x0) угловой коэффициент касательной (или тангенс угла наклона касательной к положительному направлению оси OX).

Монотонные функции и условия монотонности функции

Функция y =f(x) называется возрастающей на интервале (a; b), если для x1 6x2 (x1; x2 2(a; b)) выполняется неравенство f(x1)6f(x2) (большему значению аргумента соответствует большее значение функции).

Функция y =f(x) называется строго возрастающей на интервале (a; b), если для x1 <x2 (x1; x2 2(a; b)) выполняется неравенство f(x1)<f(x2).

Функция y =f(x) называется убывающей на интервале (a; b), если для x1 6x2 (x1; x2 2(a; b)) выполняется неравенство f(x1)>f(x2) (большему значению аргумента соответствует меньшее значение функции).

Функция y =f(x) называется строго убывающей на интервале (a; b), если для x1 <x2 (x1; x2 2(a; b)) выполняется неравенство f(x1)>f(x2).

Функции возрастающие или убывающие на интервале (a; b) называются монотонными на (a; b).

Пусть функция y =f(x) определена и дифференцируема на (a; b). Она является возрастающей на (a; b) в том и только в том случае, когда производная f0(x)>0 на

(a; b).

Функция y =f(x) является убывающей на (a; b) только тогда, когда f0(x)60 на

(a; b).

Таким образом у монотонной функции производная сохраняет знак.

139

Экстремумы функций

Точка x0 является точкой (локального) максимума для функции y =f(x), если найдется такой интервал (a; b), x0 2(a; b), что выполнено неравенство

f(x)6f(x0) для всех точек x2(a; b);

принадлежащих ОДЗ функции. Значение f(x0) называют максимальным значением функции.

Точка x0 является точкой (локального) минимума для функции y =f(x), если найдется такой интервал (a; b), x0 2(a; b), что выполнено неравенство

f(x)>f(x0) для всех точек x2(a; b);

принадлежащих ОДЗ функции. Значение f(x0) называют минимальным значением функции.

Точки максимума и минимума называются точками (локального) экстремума, а значения функции в этих точках экстремальными значениями функции.

Определения точек максимума и минимума являются локальными (т. е. зависят от поведения функции вблизи этих точек), поэтому у функции может быть несколько максимумов и несколько минимумов в области допустимых значений. Функция также может иметь несколько экстремальных значений в ОДЗ.

Значение функции, которое превосходит все остальные значения функции в ОДЗ называется наибольшим значением функции.

Значение функции, которое меньше либо равно всех остальных значений функции в ОДЗ называется наименьшим значением функции.

С помощью производных можно находить экстремумы функции.

Пусть функция y =f(x) дифференцируема на (a; b) и точка x0 2(a; b) является точкой экстремума, тогда f0(x0)=0 (это необходимое условие экстремума функции).

Данное условие не всегда является достаточным.

Точка x0 называется критической для функции y =f(x), если производная функции f(x) в этой точке равна нулю или не существует.

Критические точки являются точками "подозрительными"на экстремум.

Пусть функция y =f(x) определена и дифференцируема на (a; b), точка x0 2(a; b) является критической для данной функции. Если при переходе через критическую точку производная f0(x) меняет знак, то x0 является точкой экстремума, а именно, максимума, если знак меняется с плюса на минус, и минимума, если знак меняется с минуса на плюс. Если же при переходе через критическую точку производная знака не меняет, то x0 не является точкой экстремума (это достаточное условие существования экстремума функции).

Общая схема исследования функции на экстремум заключается в следующем:

1.Находим критические точки функции.

2.Проверяем достаточное условие существования экстремума в критических точ-

ках.

Если нужно найти наибольшее и наименьшее значения функции на отрезке [a; b], то к критическим точкам нужно добавить еще концы этого отрезка. Сравнить значения функции в критических точках и в граничных точках, выбрать из них наименьшее и наибольшее значения.

140