1.4. Законы распределений св

1. Закон равномерного распределения вероятностей

Распределение вероятностей называется равномерным, если на интервале, которому принадлежат все возможные значения СВ, плотность распределения сохраняет постоянное значение.

Если все возможные значения СВ принадлежат отрезку , на котором функцияf(x) сохраняет постоянное значение, то плотность вероятности:

Функция распределения
Математическое ожидание ; дисперсия .

Пример 7. Поезда метрополитена идут регулярно с интервалом 2 минуты. Пассажир выходит на платформу в случайные моменты времени. Какова вероятность, что ждать пассажиру придется не более 0,5 мин. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение СВ Х – времени ожидания поезда.

Решение. СВ Х – время ожидания на временном отрезке имеет равномерный закон распределения. Вероятность того, что пассажир будет ждать не более 0,5 минуты равна

Матем.ожидание , дисперсия

2. Нормальный закон распределения

Нормальный закон распределения (нормальное распределение, распределение Гаусса) наиболее часто встречается на практике. Он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.

Опр. Нормальным называется распределение вероятностей непрерывной СВ, которое описывается плотностью .

Оно определятся двумя параметрами: а и σ.

Вероятностный смысл этих параметров: а = М(Х), σ² = D(X), т.е. σ – среднее квадратическое отклонение.

Функция нормального распределения F(x) = .

Кривую нормального закона распределения называют нормальной (или кривой Гаусса).

Рассмотрим как меняется нормальная кривая при изменении параметров а и σ:

Если σ=const и меняется а: Меняется центр симметрии.

Если а = const и меняется σ: При увеличении σ кривая станет более плоской.

Т.о. параметр а (т.е. М(Х)) характеризует положение, а параметр σ (среднее квадратическое отклонение ) форму нормальной кривой.

Нормальное распределение с параметрами а и σ обозначается N(а; σ).

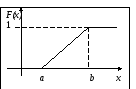
Если параметры а = 0, σ = 1, то нормальный закон распределения называется стандартным или нормированным N(0; 1). А кривая – стандартной.

Плотность нормированного распределения (функция Лапласа, приложение 1) Функция распределения .

Вероятность попадания нормированной СВ Х в интервал (0, х) можно найти, используя функцию Лапласа Ф(х): Р(0 < Х < х) = .

Функция распределения СВ Х, распределенная по нормальному закону, выражается через функцию Лапласа по формуле: .

Свойства СВ, распределённой по нормальному закону:

1. Вероятность попадания СВ Х, распределённой по нормальному закону, в интервал [x1; x2], равна , .

2. Вероятность того, что отклонение СВ Х, распределенной по нормальному закону, от МО а не превысит величину  > 0 ( по абсолютной величине)

В частности, если  = σ: ;  = 2σ: ;  = 3σ: . «Правило трёх сигм»: Если СВ Х имеет нормальный закон N(а; σ), то практически достоверно, что её значения заключены в интервале (а – 3σ ; а + 3σ). Нарушение правила является событием практически невозможным .

Пример 8. Полагая, что рост мужчин определённой возрастной группы имеет нормальное распределение СВ Х с параметрами а = 173, σ² = 36, найти:

а) долю костюмов 4-го роста (176 – 182), которые нужно предусмотреть в общем объёме производства. б) сформулировать «правило 3-х сигм».

Решение. а) Р(176 Х  182) = Ф(t₂) – Ф(t₁) = Ф(1,5) – Ф(0,5) = 0,2418.

(где ,).

б) Практически достоверно, что рост мужчин данной возрастной группы заключен в границах от а – 3σ = 173 – 36 = 155 см до а + 3σ = 173 + 36 = 191см.
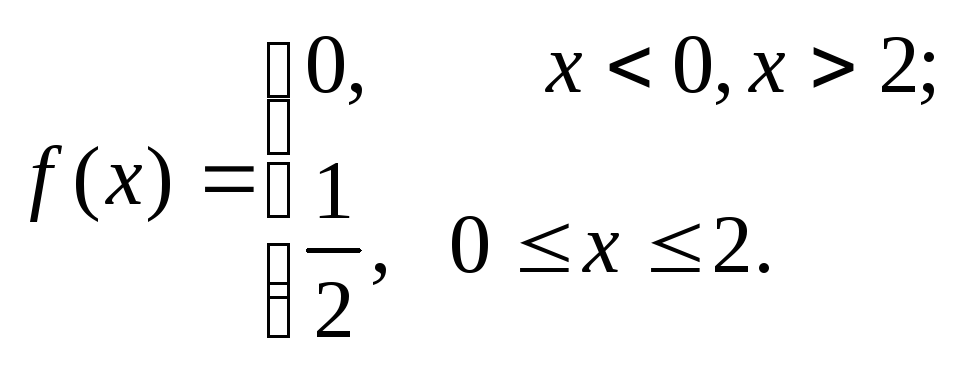