Эконометрика, лекции

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Составитель: Е.А.Парышева

Введение Эконометрика – наука, исследующая количественные закономерности и взаимозависи-

мости в экономике на основе методов теории вероятностей и математической статистики, адаптированных к обработке экономических данных.

Основным элементом курса является анализ и построение взаимосвязей экономических переменных.

Математическая статистика и ее применение в экономике – эконометрика – позволяют строить экономические модели, оценивать их параметры, проверять гипотезы о свойствах экономических показателей и формах их связи, что в конечном счёте служит основой для экономического анализа и прогнозирования (основная цель эконометрики).

Экономические модели позволяют выявить особенности экономического объекта и на основе этого предсказывать будущее поведение объекта при изменении каких-либо параметров (повышение обменного курса, падение прибыли…).

По своему определению любая экономическая модель абстрактна и, следовательно, неполна. Так, например, в простейшей модели спроса предполагают, что спрос на какой-либо товар определяется его ценой (р) и доходом потребителя (I): q f ( p, I ) .

На самом же деле на спрос влияют также другие факторы (цены на другие товары, реклама, мода, погода и т.д.). Поэтому в модель добавляют, обычно аддитивным образом, случайный компонент ε, интегрирующий (объединяющий) в себе влияние всех неучтённых явно в модели факторов. Например, модель спроса принимает вид: q f ( p, I ) .

Введение случайного компонента в модель приводит к тому, что взаимосвязь остальных её переменных перестаёт быть строго детерминированной (функциональной) и становится стохастической (статистической, случайной), каковая и наблюдается в реальной действительности.

Связь переменных, на которую накладываются воздействия случайных факторов, называ-

ется статистической (корреляционной).

Основой для выявления и обоснования эмпирических (опытных) закономерностей являются статистические данные, которые обычно подразделяются на 2 вида:

-перекрёстные данные – данные по какому-либо экономическому показателю, полученные для различных однотипных объектов (фирм, регионов). При этом либо все данные относятся к одному периоду времени, либо временная принадлежность несущественна.

-временные ряды – данные, характеризующие один объект, но в разные моменты време-

ни.

Существуют различные методы сбора экономических данных: опрос, анкетирование, получение официальной стат.отчётности…

Собранные данные могут быть представлены в различной форме: в виде таблиц, диаграмм, графиков.

Далее подготовленные данные подставляются в теоретическую модель, представленную аналитически (в виде некоторого уравнения) или в графическом виде.

При этом возникает ряд проблем, важнейшими из которых являются проверка согласованности теоретической модели с опытными данными, оценка параметров модели и проверка предположений (гипотез), лежащих в основе модели.

Основные этапы эконометрического исследования:

0. Постановочный этап – постановка проблемы, целей моделирования, сбор данных, анализ их качества.

I. Спецификация модели – выбор вида формулы зависимости.

II. Параметризация – оценка значений параметров выбранной модели.

III. Верификация – проверка качества полученных параметров и самой модели в целом. IV. Использование построенной модели для объяснения поведения экономических пока-

зателей и прогнозирования.

1

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Основные типы моделей:

Экономико-математическая модель – это математическое описание какого-либо экономического процесса или объекта.

Математические модели, используемые в экономике, можно подразделить на классы по ряду признаков, относящихся к особенностям моделируемых объектов, цели моделирования и используемого инструментария.

-Макроэкономические модели описывают экономику как единое целое, связывая между собой укрупнённые материальные и финансовые показатели (ВВП, потребление, инвестиции, занятость, процентную ставку…).

Микроэкономические модели описывают взаимодействие структурных и функциональных составляющих экономики, либо поведение отдельной такой составляющей в рыночной среде.

-Теоретические модели позволяют изучать общие свойства экономики и её характерных элементов дедукцией (от общего к частному) выводов из формальных предпосылок.

Прикладные модели оценивают параметры функционирования конкретного экономического объекта и позволяют сформулировать рекомендации для практических решений. К прикладным относятся прежде всего эконометрические модели, оперирующие числовыми значениями экономических переменных и позволяющие статистически значимо оценивать их на основе имеющихся наблюдений.

Особое место в рыночной экономике занимают равновесные модели, которые описывают такие состояния экономики, когда результирующая всех сил, стремящихся вывести их из этого состояния, равна 0.

-Статические модели описывают состояние экономического объекта в конкретный момент или период времени.

Динамические модели включают взаимосвязи переменных во времени.

-Детерминированные модели предполагают строгие функциональные связи между переменными.

Стохастические допускают наличие случайных воздействий на исследуемые показатели и используют инструментарий теории вероятностей и математической статистики для их описания.

Приведём 3 основных класса моделей, которые применяются для анализа и прогнозирования в эконометрике:

1. Модели временных рядов: модели тренда у(t) T (t) t и сезонности у(t) S(t) t .

Они объясняют поведение временного ряда, исходя только из его предыдущих значений. Применяются для изучения и прогнозирования объёма продаж билетов, спроса, прогнозирования % ставки.

2. Регрессионные модели с 1 уравнением: зависимая переменная у представляется в виде функции одной или нескольких переменных: y f (x, ) f (x1 ,..., xn ; 1 ,..., n ) , где у – объяс-

няемая (зависимая) переменная, x1 ,..., xn - объясняющие (независимые) переменные, 1 ,..., n - параметры уравнения.

Регрессионные уравнения – уравнения статистической связи между переменными.

В зависимости от вида функции f модели делятся на линейные и нелинейные. Эти модели применяют значительно шире, чем модели временных рядов. (Например, спрос на мороженое как функция от времени, температуры воздуха, среднего уровня доходов…).

3. Системы одновременных уравнений: описываются системами уравнений, могут состоять из тождеств и регрессионных уравнений, которые кроме объясняющих переменных могут включать в себя объясняемые переменные из других уравнений.

2

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Тема 1. Основные понятия теории вероятностей 1.1. Вероятностный эксперимент, событие, вероятность.

Испытание (вероятностный эксперимент) – действие, результат которого заранее не известен (т.к. он является случайным).

Элементарный исход – возможный результат испытания. Событие – один или несколько исходов.

Событие называется случайным, если при осуществлении определенной совокупности условий S оно может либо произойти, либо не произойти. Далее вместо того, чтобы говорить «совокупность условий S осуществлена», будем говорить: «произведено испытание».

Например, строительство автомобильного завода в контексте получения прибыли – вероятностный эксперимент (испытание). Получение прибыли – случайное событие.

Если событие происходит всегда в условиях данного эксперимента, то оно называется достоверным (спрос на автомобили упадет при резком повышении цен на автомобили). Событие называется невозможным, если оно никогда не произойдет в условиях данного эксперимента (рост спроса на автомобили приведет к снижению их цены при прочих равных условиях – невозможное событие).

События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании (увеличение налогов – рост располагаемого дохода).

Иначе события называются совместными (увеличение объема продаж – увеличение прибыли).

Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них (появление хотя бы одного из событий полной группы есть достоверное событие).

Если события, образующие полную группу несовместные, то в результате испытания появится только одно из них.

Противоположными называют два единственно возможных события, образующих пол-

ную группу. Противоположные события принято обозначать А и А .

События называются равновозможными, если ни одно из них не является более возможным, чем другое.

Каждый из возможных результатов испытания называется элементарным исходом (элементарным событием) (их нельзя разбить на более простые).

Вероятность - число, характеризующее степень возможности появления события. Вероятностью события А называют отношение числа благоприятствующих этому собы-

тию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.

Р(А) т(А) , где m(A) – число благоприятствующих событию А исходов, n – число всех

п

возможных элементарных исходов.

Свойства вероятности:

1.Вероятность достоверного события равна единице.

2.Вероятность невозможного события равна 0.

3.Вероятность случайного события: 0 < P(A) < 1.

4.Вероятность любого события удовлетворяет двойному неравенству: 0≤ P(A) ≤ 1.

5.Если А и А - противоположные, то Р(А) = 1 – Р( А ).

Наряду с классическим определением используют и другие определения вероятности, в частности статистическое определение: в качестве статистической вероятности события принимают относительную частоту или число, близкое к ней.

Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведённых испытаний.

3

Generated by Foxit PDF Creator © Foxit Software http://www.foxitsoftware.com For evaluation only.

W(A) = m , m – число появлений события, n – общее число испытаний. n

Вероятность вычисляют до опыта, а относительную частоту – после опыта.

Пример 1. Отдел технического контроля обнаружил 3 нестандартных детали в партии из 80 случайно отобранных деталей. Относительная частота появления нестандартных деталей

W(A) = 3 .

80

Свойство устойчивости относительной частоты: в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Это постоянное число и есть вероятность появления события.

Т.о., если опытным путём установлена относительная частота, то полученное число можно принять за приближённое значение вероятности.

Статистическая вероятность любого события также заключена между нулём и единицей:

0 ≤ m ≤ 1. n

Для существования статистической вероятности требуется:

А) возможность производить неограниченное число испытаний, в каждом из которых событие А наступает или не наступает;

Б) устойчивость относительных частот появления А в различных сериях достаточно большого числа испытаний.

1.2. Случайные величины Случайной называют величину, которая в результате испытания примет одно и только

одно возможное значение, наперед не известное и зависящее от случайных причин, которые сначала не могут быть учтены.

Пример 2. Число родившихся детей в городе в течение суток – СВ, которая принимает значения 1, 2, 3, …

Пример 3. Прибыль фирмы – СВ. Возможные значения этой величины принадлежат некоторому промежутку.

Будем обозначать случайные величины прописными буквами X, Y, Z…, а их возможные значения соответствующими строчными буквами x, y, z…

Различают следующие виды случайных величин:

Дискретная (прерывная) СВ – величина, которая принимает отдельные, изолированные числовые значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. (Пр.2)

Непрерывная случайная величина – СВ, которая может принимать любые числовые значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной СВ бесконечно. (Пр. 3).

Для задания дискретной СВ недостаточно перечислить все возможные ее значения, нужно еще указать их вероятности.

Законом распределения дискретной СВ называют соответствие между возможными значениями этой величины и их вероятностями. Закон распределения можно задать таблично, аналитически и графически.

При табличном задании первая строка таблицы содержит возможные значения, а вторая – их вероятности:

Т.к. в одном испытании случайная величина принимает одно и только одно возможное значение, то события Х = х1, Х = х2,…, Х = хn образуют полную группу. => Сумма вероятностей этих событий равна 1: р1 р2 ... рп 1.

4

Generated by Foxit PDF Creator © Foxit Software http://www.foxitsoftware.com For evaluation only.

Если множество возможных значений Х бесконечно (счетно), то ряд р1 р2 ... сходится, и его сумма равна 1.

Пример 4. В денежной лотерее выпущено 100 билетов. Разыгрывается 1 выигрыш в 50 рублей и 10 выигрышей по 5 руб. Найти закон распределения СВ Х – стоимости возможного выигрыша владельца лотерейного билета.

Решение. Х – дискретная СВ. Ее возможные значения: х1= 0, х2 =5, х3 = 50. Вероятности этих значений: р1= 0,89, р2 = 0,1, р3 = 0,01. (проверка: 0,89 + 0,1 + 0,01 = 1)

Тогда закон распределения:

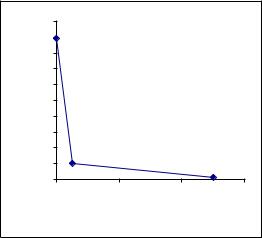
Для наглядности закон распределения дискретной СВ можно изобразить и графически, для чего в прямоугольной системе координат строят точки (xi, pi), а затем соединяют их отрезками. Полученная ломанная называется многоугольником или полигоном распределения.

Пр.4.

Аналитически СВ задается либо функцией распределения, либо плотностью вероятностей. Функцией распределения СВ Х называют функцию F(x) , определяющую вероятность то-

го, что СВ Х принимает значение, меньшее, чем х: F(x) P(X x) .

Иногда эту функцию называют функцией накопленной вероятности или кумулятивной функцией распределения.

Свойства функции распределения:

1.0 ≤ F(x) ≤ 1.

2.F(x) - неубывающая функция, т.е. x1 x2 F(x1) F(x2 ) .

4.P(a X b) F(b) F(a) .

5.P(X х) 1 F(х) .

График функции распределения даёт наглядное представление о вероятности изменения значений СВ.

Для примера функция распределения и её график имеют вид:

5

Для непрерывной СВ нельзя определить вероятность того, что она принимает некоторое конкретное значение, а следовательно непрерывную СВ нельзя задать таблично. Поэтому для описания непрерывной СВ может быть использована функция распределения. При этом она является непрерывной неубывающей функцией, изменяющейся от 0 до 1.

Плотностью вероятности (плотностью распределения вероятностей) непрерывной СВ

Х называют функцию f (x) F (x) . Свойства плотности вероятности:

F(a)

Площадь под графиком кривой плотности вероятности равна единице.

b

Площадь заштрихованной области на рисунке равна: S f (x)dx = P(a X b) .

a

Вероятность попадания значений СВ в «хвосты» распределения, т.е. в интервалы ( ;а) и (b; ) , равна 1 – P(a X b) . Т.о. с помощью плотности вероятности можно определить вероятность попадания непрерывной СВ Х в заданный интервал P(a X b) , что имеет большое прикладное значение.

1.3. Числовые характеристики СВ

Числовыми характеристиками СВ называют числа, которые описывают СВ суммарно. К таким числовым характеристикам относится математическое ожидание. Оно характеризует среднее ожидаемое значение СВ, т.е. приблизительно равно его среднему значению. Для решения многих задач достаточно знать МО (например, при оценивании покупательной способности населения достаточно знать средний доход).

6

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Математическим ожиданием дискретной СВ называют сумму произведений всех возможных ее значений на их вероятности.

n

М (Х ) х1 р1 х2 р2 ... хп рп xi pi .

i 1

Если дискретная СВ принимает счетное множество всевозможных значений, то

М(Х ) xi pi

i1

Причем мат.ожидание существует, если ряд в правой части сходится абсолютно.

Для непрерывной СВ: M(X) = х f (x)dx .

Замечание. Мат.ожидание – неслучайная постоянная величина.

Пример 5. Найти мат.ожидание дискретной СВ Х, зная закон ее распределения:

Решение. Искомое мат.ожидание М(Х) = 3∙0,1 + 5∙0,6 + 2∙0,3 = 3,9.

Мат.ожидание числа появления события в одном испытании равно вероятности этого события.

Мат.ожидание приближенно равно (тем больше, чем больше число испытаний) среднему арифметическому наблюдаемых значений СВ.

Замечание. МО больше наименьшего и меньше наибольшего возможных значений СВ.

Свойства математического ожидания:

1.Мат.ожидание постоянной величины равно самой постоянной: М(С) = С.

2.Постоянный множитель можно выносить за знак МО: М(СХ) = СМ(Х).

3.МО суммы 2-х СВ равно сумме МО слагаемых: М(Х + Y) = M(X) + M(Y).

4.МО произведения двух независимых СВ равно произведению их МО:

М(ХY) = M(X)M(Y).

Зная только МО СВ нельзя судить ни о том, какие значения принимает СВ, ни о том, как

эти значения рассеяны вокруг мат.ожидания. Т.е. МО полностью не характеризует СВ. Поэтому наряду с мат.ожиданием вводят и другие числовые характеристики. Например, чтобы оценить, как рассеяны величины вокруг МО, используют дисперсию.

Дисперсией СВ называют мат.ожидание квадрата отклонения СВ от ее МО:

D(X ) M X M (X ) 2 M (X 2 ) M (X ) 2 .

При этом для дискретной СВ:

Решение. Найдем МО: М(Х) = 1∙0,3 + 2∙0,5 + 5∙0,2 = 2,3.

Затем найдем возможные значения квадрата отклонения:

[х1 – M(X)]2 = (1 – 2,3)2 = 1,69; [х2 – M(X)]2 = (2 – 2,3)2 = 0,09; [х3 – M(X)]2 = (5 – 2,3)2 = 7,29.

Тогда, D(X) = 1,69∙0,3 + 0,09∙0,5+ 7,29∙0,2 = 2,01.

2 способ. М(Х) = 2,3. Вычислим M(X2) = 12 0,3 22 0,5 52 0,2 7,3. Искомая дисперсия равна D(X) = 7,3 – (2,3)2 = 7,3 – 5,29 = 2,01.

7

Дисперсия имеет размерность, равную квадрату размерности СВ.

Кроме дисперсии для оценки рассеяния СВ вокруг ее среднего значения служат и другие характеристики, например, среднее квадратическое отклонение.

Средним квадратическим отклонением СВ Х называют квадратный корень из ее дис-

Чтобы оценить разброс значений СВ в процентах относительно её среднего значения, вводится коэффициент вариации V(X), который рассчитывается по формуле:

V (X ) (X ) 100% .

M (X )

1.4.Законы распределений СВ

1.Закон равномерного распределения вероятностей

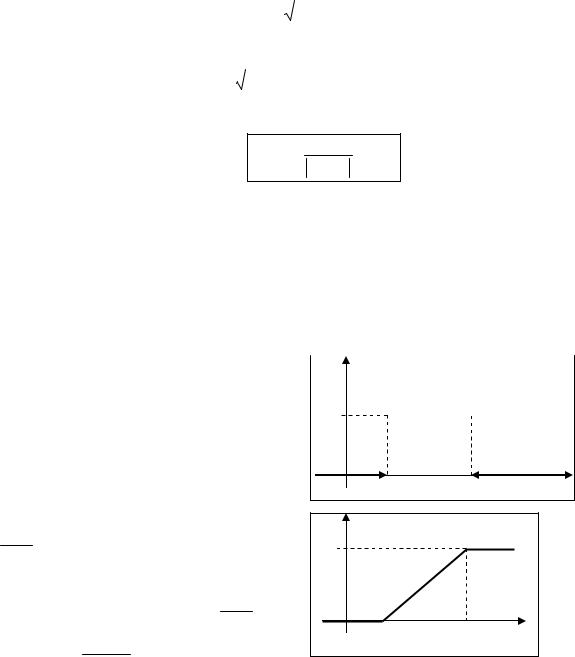
Распределение вероятностей называется равномерным, если на интервале, которому принадлежат все возможные значения СВ, плотность распределения сохраняет постоянное значение.

Если все возможные значения СВ принадлежат отрезку a,b , на котором функция f(x) сохраняет постоянное значение, то плотность вероятности:

Пример 7. Поезда метрополитена идут регулярно с интервалом 2 минуты. Пассажир выходит на платформу в случайные моменты времени. Какова вероятность, что ждать пассажиру придется не более 0,5 мин. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение СВ Х – времени ожидания поезда.

8

2. Нормальный закон распределения

Нормальный закон распределения (нормальное распределение, распределение Гаусса) наиболее часто встречается на практике. Он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.

Опр. Нормальным называется распределение вероятностей непрерывной СВ, которое

Оно определятся двумя параметрами: а и σ.

Вероятностный смысл этих параметров: а = М(Х), σ2 = D(X), т.е. σ – среднее квадратическое отклонение.

Кривую нормального закона распределения называют нормальной (или кривой Гаусса).

Рассмотрим как меняется нормальная кривая при изменении параметров а и σ: Если σ=const и меняется а: Если а = const и меняется σ:

Т.о. параметр а (т.е. М(Х)) характеризует положение, а параметр σ (среднее квадратическое отклонение ) форму нормальной кривой.

Нормальное распределение с параметрами а и σ обозначается N(а; σ).

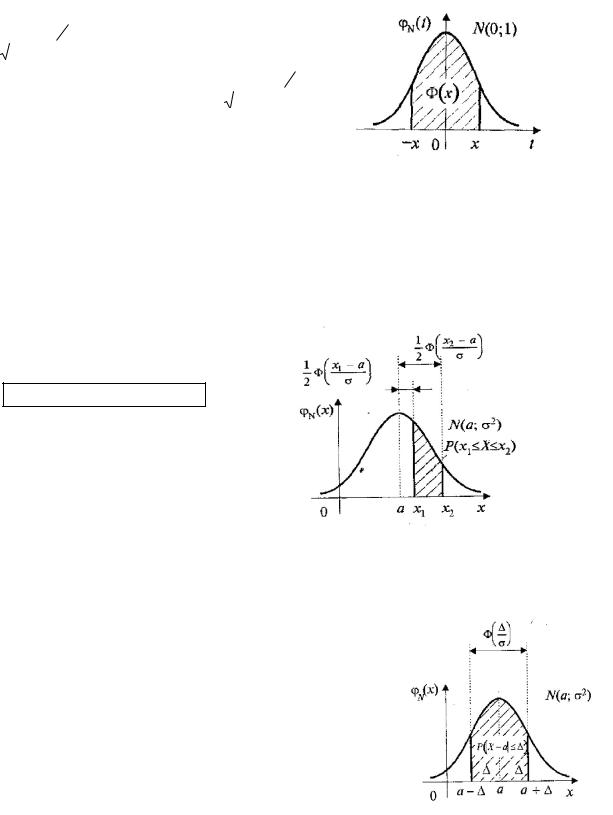
Если параметры а = 0, σ = 1, то нормальный закон распределения называется стандарт-

ным или нормированным N(0; 1). А кривая – стандартной.

9

Вероятность попадания нормированной СВ Х в интервал (0, х) можно найти, используя

х

функцию Лапласа Ф(х): Р(0 < Х < х) = (z)dz (x) .

0

Функция распределения СВ Х, распределенная по нормальному закону, выражается через

Свойства СВ, распределённой по нормальному закону: 1. Вероятность попадания СВ Х, распре-

делённой по нормальному закону, в интервал [x1; x2], равна

P(х1 Х х2 ) (t2 ) (t1)

2. Вероятность того, что отклонение СВ Х, распределенной по нормальному закону, от МО а не превысит величину > 0 ( по абсолютной величине)

Пример 8. Полагая, что рост мужчин определённой возрастной группы имеет нормальное распределение СВ Х с параметрами а = 173, σ2 = 36, найти:

а) долю костюмов 4-го роста (176 – 182), которые нужно предусмотреть в общем объёме производства. б) сформулировать «правило 3-х сигм».

Решение. а) Р(176 Х 182) = Ф(t2) – Ф(t1) = Ф(1,5) – Ф(0,5) = 0,2418.

10