Эконометрика, лекции

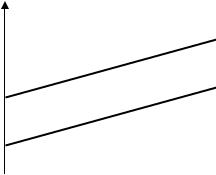
Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

признаку. При g>0 она будет в пользу мужчин, при g<0 – в пользу женщин. На графике такие зависимости изображаются параллельными прямыми.

y

a+g

a

0 x

Нулевой уровень (z = 0) качественной переменной называется базовым или сравнительным.

Коэффициент g в модели называется дифференциальным коэффициентом свободного члена, т.к. он показывает, на сколько отличается свободный член в модели при значении z = 1 от свободного члена при базовом значении фиктивной переменной.

Кроме того, значения фиктивных переменных можно изменять на противоположные. Суть модели от этого не изменится. Изменится только знак коэффициента g в модели.

3. С помощью большего числа фиктивных переменных можно обрисовать более сложные ситуации.

В этом случае может возникнуть ситуация, которая называется ловушкой фиктивной переменной. Она возникает, когда для моделирования k значений качественного признака используется ровно k бинарных (фиктивных) переменных. В этом случае одна из таких переменных линейно выражается через все остальные, и матрица значений переменных становится вырожденной. Тогда исследователь попадает в ситуацию совершенной мультиколлинеарности. Избежать подобной ловушки позволяет правило:

Если качественная переменная имеет k альтернативных значений, то при моделировании используется только (k-1) фиктивных переменных.

Например, если качественная переменная имеет 3 уровня, то для моделирования достаточно двух фиктивных переменных z1 и z2. Тогда для обозначения третьего уровня достаточно принять, например, обе переменные равными нулю: z1=z2=0. В частности, для обозначения уровня экономического развития страны (развитая, развивающаяся или страна «третьего мира») можно использовать обозначения:

Тогда z1=z2=0 означает страну «третьего мира».

Рассмотрим модель с двумя объясняющими переменными, одна из которых количественная, а другая – фиктивная, причем имеющая 3 альтернативы. Например, расходы на содержание ребёнка могут быть связаны с доходами домохозяйств и возрастом ребёнка: дошкольный, младший школьный и старший школьный.

Т.к. качественная переменная связана с 3 альтернативами, то по общему правилу моделирования необходимо использовать 2 фиктивные переменные:

у a bx g1 z1 g2 z2 e , где у – расходы на содержание ребёнка, х – доходы домохо-

зяйств,

Тогда образуются частные уравнения регрессии для отдельного возраста:

61

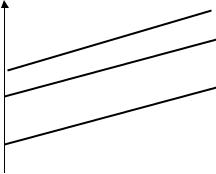
Базовым значением качественной переменной является значение «дошкольник», g1 , g2 -

дифференциальные свободные члены. Т.о. получаем три параллельные регрессионные прямые:

y

a+g1+g2

a+g1

a

0 x

После вычисления коэффициентов регрессий определяется статистическая значимость g1 , g2 на основе обычных t – статистик. Если они оказываются статистически незначимыми, то можно сделать вывод, что возраст ребёнка не оказывает существенного влияния на расходы по его содержанию.

4. В отдельных случаях может оказаться необходимым введение двух и более фиктивных переменных.

Для простоты рассмотрим регрессию с одной количественной и двумя качественными переменными. Пусть у – заработная плата сотрудников, х – стаж работы, z1 – наличие высшего образования, z2 – пол сотрудника.

- зарплата мужчины с высшим образованием: уˆ (a g1 g2 ) bx (z1 1, z2 1) . Очевидно, что все отдельные регрессии отличаются друг от друга только свободным чле-

ном. Определение статистической значимости коэффициентов показывает, влияют ли образование и пол сотрудника на его зарплату.

5. Фиктивные переменные широко используются и для оценки сезонных различий в потреблении. Например, спрос на туристические путёвки, охлаждённую воду, мороженное существенно выше летом, чем зимой. Спрос на обогреватели, шубы – наоборот.

Обычно сезонные колебания характерны для временных рядов. Устранение и нейтрализация сезонного фактора позволяет сконцентрироваться на других важных количественных и качественных характеристиках модели (тренде).

Устранение сезонного фактора называется сезонной корректировкой. Существует несколько методов сезонной корректировки, одним из которых является метод фиктивных пе-

ременных.

Пусть у зависит от количественной переменной х, причём зависимость отличается по кварталам, тогда общую модель можно представить в виде:

уt a bxt g1 z1t g2 z2 t g3 z3t et ,

62

6. Иногда (достаточно редко) фиктивные переменные могут быть использованы для объяснения поведения зависимой переменной (т.е. зависимая переменная является фиктивной).

Например, исследуется зависимость наличия автомобиля от дохода, пола субъекта и т.п.

Наибольшими прогностическими возможностями обладают модели, зависящие от нескольких количественных факторов и от нескольких фиктивных.

Влияние качественного фактора может сказываться не только на значении свободного члена, но и на угловом коэффициенте линейной регрессионной модели. Обычно это характерно для временных рядов экономических данных при изменении институциональных условий, введении новых правовых или налоговых ограничений. Тогда зависимость может быть выражена

В этой ситуации ожидаемое значение зависимой переменной определяется следующим образом:

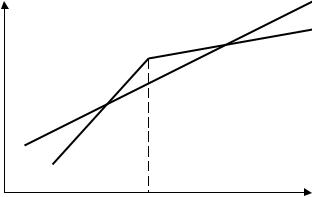
членом и дифференциальным угловым коэффициентом. Фиктивная переменная разбивает зависимость на две части – до и после внесения изменений в условия её действия.

3

у

2

Общая зависимость имеет вид кусочно – линейной функции, а изменения условий отображаются изменением угла наклона прямой к оси абсцисс (линии 1 – 2).

63

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Здесь исследователь должен принять решение, стоит ли разбивать выборку на части и строить для каждой из них уравнение регрессии (прямые 1 и 2) или ограничиться одной общей линией регрессии (линия 3). Для этого используют тест Чоу, который опирается на F–

статистику F s0 s1 s2 n 2m 2 , (см. тема «Статистика Фишера в регрессионном анали-

зе»).

Если гипотеза о структурной стабильности выборки отклоняется, то исследуется вопрос о причинах структурных различий в подвыборках. Пусть данные в подвыборках описываются

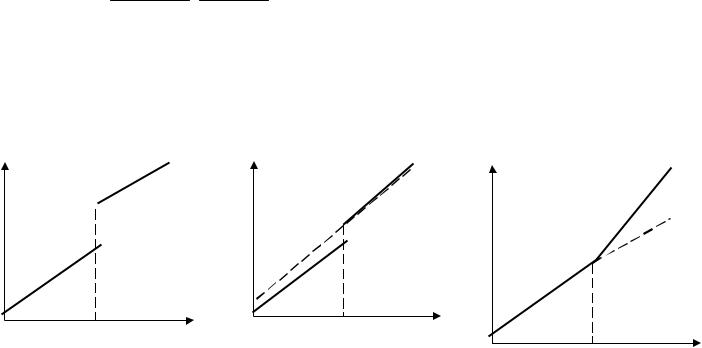
Тогда возможны следующие варианты:

Для тестирования всех этих ситуаций применяется следующая методика, предложенная Гуйарати. Она основана на включении в модель регрессии фиктивной переменной z, которая равна 1 для всех x<x* и равна 0 для всех x>x*. Далее определяются параметры следующего

Следовательно, параметр b есть разница между a1 и а2, параметр d – разница между b1 и b2. Если в уравнении b является статистически значимым, а d – нет, то имеем первый вариант структурной перестройки. Если, наоборот, статистически значимым является d, а b – незначим, имеем второй вариант структурных изменений. Наконец, третий вариант имеем в случае, если оба коэффициента b и d являются статистически значимыми.

В заключение следует отметить, что преимущество метода Гуйарати перед тестом Чоу состоит в том, что нужно построить только одно, а не три уравнения регрессии.

Тема 10. СИСТЕМЫ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

10.1. Общее понятие о системах уравнений, используемых в эконометрике

Объектом статистического изучения в социальных науках являются сложные системы. Построение изолированных уравнений регрессии недостаточно для описания таких систем и объяснения механизма их функционирования.

Поэтому при моделировании экономических ситуаций часто необходимо построение систем уравнений, когда одни и те же переменные могут выступать и в роли объясняющих и в роли объясняемых. Так, если изучается модель спроса как отношение цен и количества потребляе-

64

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

мых товаров, то одновременно для прогнозирования спроса необходима модель предложения товаров, в которой рассматривается также взаимосвязь между количеством и ценой предлагаемых благ. Это позволяет достичь равновесия между спросом и предложением.

Система уравнений в эконометрических исследованиях может быть построена поразному.

Системы уравнений здесь могут быть построены по-разному.

Возможна система независимых уравнений, когда каждая зависимая переменная y рассматривается как функция одного и того же набора факторов x:

Набор факторов xj в каждом уравнении может варьироваться.

Каждое уравнение системы независимых уравнений может рассматриваться самостоятельно. Для нахождения его параметров используется МНК. По существу, каждое уравнение этой системы является уравнением регрессии.

Если зависимая переменная y одного уравнения выступает в виде фактора x в другом уравнении, то исследователь может строить модель в виде системы рекурсивных уравнений:

y1 a11x1 a12 x2 ... a1n xn 1,

y2 b21 y1 a21x1 a22 x2 ... a2n xn 2 , (2)

y3 b31 y1 b32 y2 a21x1 a22 x2 ... a2n xn 2 ,

.........................................................................

В данной системе зависимая переменная y включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором факторов x . Каждое уравнение этой системы может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов (МНК).

Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях – в правую часть системы:

Система взаимозависимых уравнений получила название системы совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других.

Вэконометрике эта система уравнений называется также структурной формой модели.

Вотличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим. С этой целью используются специальные приемы оценивания.

10.2. Структурная и приведенная формы модели

Экономическая модель как система одновременных уравнений может быть представлена в структурной или приведённой форме. В структурной форме её уравнения имеют исходный вид, отражая непосредственную связь между переменными.

65

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Структурная форма модели обычно содержит эндогенные и экзогенные переменные. Эндогенные переменные (внутренние) – это зависимые переменные, число которых

равно числу уравнений в системе. Они обозначаются через y.

Экзогенные переменные (внешние) – это предопределенные переменные (задаваемые извне, независимые), влияющие на эндогенные переменные. Они обозначаются через x.

Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, а в других – как экзогенные переменные. Внеэкономические переменные (например, климатические условия) входят в систему как экзогенные переменные. В качестве экзогенных переменных можно рассматривать значения эндогенных переменных за предшествующий период времени (лаговые переменные). Например, потребление текущего года yt может зависеть также и от уровня потребления в предыдущем году yt-1.

Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных.

Простейшая структурная форма модели имеет вид:

где y1,y2 – эндогенные переменные, x1,x2 – экзогенные.

Коэффициенты bik при эндогенных и aij – при экзогенных переменных называются

структурными коэффициентами модели. Все переменные в модели выражены в отклонениях (x x) и (y y) от среднего уровня, поэтому свободный член в каждом уравнении отсутст-

вует.

Использование МНК для оценивания структурных коэффициентов модели дает смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма преобразуется в приведенную.

Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:

yˆ1 11x1 ... 1m xm,

уˆ2 21х1 ... 2m xm, (5)

yˆn n1x1 ... nm xm.

ij коэффициенты приведенной формы модели.

По своему виду приведенная форма модели ничем не отличается от системы независимых уравнений. Применяя МНК, можно оценить ij , а затем оценить значения эндогенных пе-

ременных через экзогенные.

Коэффициенты приведённой формы представляют собой нелинейные функции коэффициентов структурной формы модели.

Рассмотрим это положение на примере простейшей структурной модели, выразив коэффициенты приведенной формы модели через коэффициенты структурной модели.

Для структурной модели вида (4) приведенная форма модели имеет вид

66

Таким образом, можно сделать вывод о том, что коэффициенты приведенной формы модели (6) будут выражаться через коэффициенты структурной формы следующим образом:

Следует заметить, что приведенная форма модели хотя и позволяет получить значения эндогенной переменной через значения экзогенных переменных, но аналитически она уступает структурной форме модели, так как в ней отсутствуют оценки взаимосвязи между эндогенными переменными.

10.3. Проблема идентификации

При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация – это единственность соответствия между приведенной и структурной формами модели.

Структурная модель (3) в полном виде, состоящая в каждом уравнении системы из n эндогенных и m экзогенных переменных, содержит n(n-1+m) параметров. Приведенная модель (5) в полном виде содержит nm параметров. Таким образом, в полном виде структурная модель содержит большее число параметров, чем приведенная форма модели. Поэтому n(n-1+m) параметров структурной модели не могут быть однозначно определены через nm параметров приведенной формы модели.

Чтобы получить единственно возможное решение для структурной модели, необходимо предположить, что некоторые из структурных коэффициентов модели равны нулю. Тем самым уменьшится число структурных коэффициентов.

С позиции идентифицируемости структурные модели можно подразделить на три вида:

А) идентифицируемые; Б) неидентифицируемые;

В) сверхидентифицируемые.

А) Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т.е. число параметров структурной модели равно числу параметров приведенной формы модели.

67

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Б) Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели. Модель (3) в полном виде всегда неиден-

тифицируема.

В) Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе приведенных коэффициентов можно получить два или более значений одного структурного коэффициента. Сверхидентифицируемая модель, в отличие от неидентифицируемой, практически решаема, но требует для этого специальных методов исчисления параметров.

Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемой,

если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.

Необходимое условие идентифицируемости (счётное правило проверки на идентифицируемость): Обозначим Н – число эндогенных переменных в i- ом уравнении системы, D – число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение. Тогда:

D+1 = Н – уравнение идентифицируемо;

D+1 < Н – уравнение неидентифицируемо; D+1 > Н – уравнение сверхидентифицируемо.

Это счетное правило отражает необходимое, но не достаточное условие идентификации. Более точно условия идентификации определяются, если накладывать ограничения на коэффициенты матриц параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.

Для оценки параметров структурной формы система должна быть идентифицируема или сверхидентифицируема.

Пример. Проверить каждое уравнение системы на необходимое и достаточное условия идентификации:

y1 b12 y2 b13 y3 a11 x1 a12 x2

y2 b21 y1 a22 x2 a23 x3 a24 x4y3 b31 y1 b32 y2 a31 x1 a32 x2

10.4. Оценивание параметров структурной модели

Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение получили два метода оценивания коэффициентов структурной модели:

косвенный метод наименьших квадратов (КМНК);

двухшаговый метод наименьших квадратов (ДМНК);

трёхшаговый метод наименьших квадратов МНК;

метод максимального правдоподобия с полной информацией;

метод максимального правдоподобия при ограниченной информации.

Косвенный и двухшаговый методы подробно описаны в литературе и рассматриваются как традиционные методы оценки коэффициентов структурной модели.

КМНК применяется для идентифицируемой системы одновременных уравнений, а ДМНК – для оценки коэффициентов сверхидентифируемой модели.

Метод максимального правдоподобия с полной информацией рассматривается как наиболее общий метод оценивания, результаты которого при нормальном распределении призна-

68

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

ков совпадают с МНК. Однако при большом числе уравнений системы этот метод приводит к достаточно сложным вычислительным процедурам. Поэтому в качестве модификации используется метод максимального правдоподобия при ограниченной информации (метод наименьшего дисперсионного отношения), разработанный в 1949 г. Т.Андерсоном и Н.Рубиным.

В отличие от метода максимального правдоподобия в данном методе сняты ограничения на параметры, связанные с функционированием системы в целом. Это делает решение более простым, но трудоемкость вычислений остается достаточно высокой. Несмотря на его значительную популярность, к середине 60-х годов он был практически вытеснен двухшаговым методом наименьших квадратов (ДМНК) в связи с гораздо большей простотой последнего.

Дальнейшим развитием ДМНК является трехшаговый МНК (ТМНК), предложенный в 1962 г. А.Зельнером и Г.Тейлом. Этот метод оценивания пригоден для всех видов уравнений структурной модели. Однако при некоторых ограничениях на параметры более эффективным оказывается ДМНК.

Косвенный метод наименьших квадратов (КМНК) применяется в случае точно иден-

тифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов работы:

1.Структурная модель преобразовывается в приведенную форму модели.

2.Для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты ij .

3.Коэффициенты приведенной формы модели трансформируются в параметры структурной модели.

Рассмотрим применение КМНК для модели:

y1 b12 y2 a11x1 1,

у2 b21y1 a22 x2 2

Пусть мы располагаем некоторыми данными по 5 регионам:

Приведенная форма модели имеет вид:

y1 11x1 12x2 u1,

у2 21х1 22х2 u2,

где u1,u2 случайные ошибки приведенной формы модели.

Для каждого уравнения приведенной формы применим традиционный МНК и определим δ- коэффициенты. Для простоты работаем в отклонениях, т.е. y y y, х х х. Тогда систе-

ма нормальных уравнений для первого уравнения системы составит:

Для приведенных данных система составит:

5,2 11 4,2 12 6,

4,2 11 17,2 12 10.

Отсюда получаем первое уравнение (и аналогично второе):

69

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Перейдем к структурной форме следующим образом: исключим из первого уравнения приведенной формы x2 , выразив его из второго уравнения приведенной формы и подставив в первое уравнение:

x2 0,072х1 у2 . 0,00557

Первое уравнение структурной формы:

Аналогично исключим из второго уравнения x1, выразив его через первое уравнение и подставив во второе:

Эту же систему можно записать, включив в нее свободный член уравнения, т.е. перейти от переменных в виде отклонений от среднего к исходным переменным y и x :

Если к каждому уравнению структурной формы применить традиционный МНК, то результаты могут сильно отличаться. В данном примере будет:

y1 1,09 0,364у2 1,192х1 1,

у2 5,2 0,533у1 0,333х2 2

Двухшаговый МНК. ДМНК используется для сверхидентифицируемых систем. Основная идея ДМНК: на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения. Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Здесь дважды используется МНК: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной yˆi i1x1 i2 x2 ... im xm, и на вто-

ром шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных.

Сверхидентифицируемая структурная модель может быть двух типов:

-все уравнения системы сверхидентифицируемые;

-система содержит также точно идентифицируемые уравнения.

Впервом случае для оценки структурных коэффициентов каждого уравнения используется ДМНК. Во втором случае структурные коэффициенты для точно идентифицируемых уравнений находятся из системы приведенных уравнений.

ДМНК является наиболее общим и широко распространенным методом решения системы одновременных уравнений. Для точно идентифицируемых уравнений ДМНК дает тот же результат, что и КМНК.

70