5.3.3. Автокорреляция ошибок. Статистика Дарбина-Уотсона

Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Отсутствие зависимости гарантирует отсутствие коррелированности между любыми отклонениями, т.е.и, в частности, между соседними отклонениями.

Автокорреляция (последовательная корреляция) остатков определяется как корреляция между соседними значениями случайных отклонений во времени (временные ряды) или в пространстве (перекрестные данные). Она обычно встречается во временных рядах и очень редко – в пространственных данных.

Возможны следующие случаи:

Случай положительной автокорреляции ошибок регрессии, когда знаки соседних отклонений, как правило, совпадают между собой ().

Случай отрицательной автокорреляции, когда соседние отклонения имеют как правило противоположные знаки ().

Эти случаи могут свидетельствовать о возможности улучшить уравнение путём оценивания новой нелинейной формулы или включения новой объясняющей переменной.

В экономических задачах значительно чаще встречается положительная автокорреляция, чем отрицательная автокорреляция.

Если же характер отклонений случаен, то можно предположить, что в половине случаев знаки соседних отклонений совпадают, а в половине – различны.

Автокорреляция в остатках может быть вызвана несколькими причинами, имеющими различную природу.

1. Она может быть связана с исходными данными и вызвана наличием ошибок измерения в значениях результативного признака.

2. В ряде случаев автокорреляция может быть следствием неправильной спецификации модели. Модель может не включать фактор, который оказывает существенное воздействие на результат и влияние которого отражается в остатках, вследствие чего последние могут оказаться автокоррелированными. Очень часто этим фактором является фактор времени .

От истинной автокорреляции остатков следует отличать ситуации, когда причина автокорреляции заключается в неправильной спецификации функциональной формы модели. В этом случае следует изменить форму модели, а не использовать специальные методы расчета параметров уравнения регрессии при наличии автокорреляции в остатках.

Для обнаружения автокорреляции используют либо графический метод. Либо статистические тесты.

Графический метод заключается в построении графика зависимости ошибок от времени (в случае временных рядов) или от объясняющих переменных и визуальном определении наличия или отсутствия автокорреляции.

Наиболее известный критерий обнаружения автокорреляции первого порядка – критерий Дарбина-Уотсона. Статистика DW Дарбина-Уотсона приводится во всех специальных компьютерных программах как одна из важнейших характеристик качества регрессионной модели.

Сначала по построенному эмпирическому уравнению регрессии определяются значения отклонений . А затем рассчитывается статистика Дарбина-Уотсона по формуле:

.

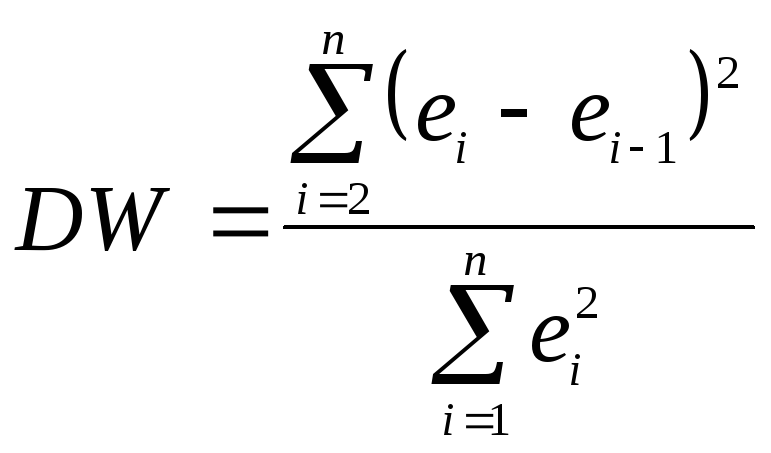Статистика DW изменяется от 0 до 4. DW=0 соответствует положительной автокорреляции, при отрицательной автокорреляции DW=4. Когда автокорреляция отсутствует, коэффициент автокорреляции равен нулю, и статистика DW = 2.

Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий.

Выдвигается гипотеза об отсутствии автокорреляции остатков. Альтернативные гипотезы исостоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам определяются критические значения критерия Дарбина-Уотсона(- нижняя граница признания положительной автокорреляции) и(-верхняя граница признания отсутствия положительной автокорреляции) для заданного числа наблюдений, числа независимых переменных моделии уровня значимости. По этим значениям числовой промежутокразбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностьюосуществляется следующим образом:

– положительная автокорреляция, принимается ;

– зона неопределенности;

– автокорреляция отсутствует;

– зона неопределенности;

– отрицательная автокорреляция, принимается .

Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу .

Можно показать, что статистика DW тесно связана с коэффициентом автокорреляции первого порядка:

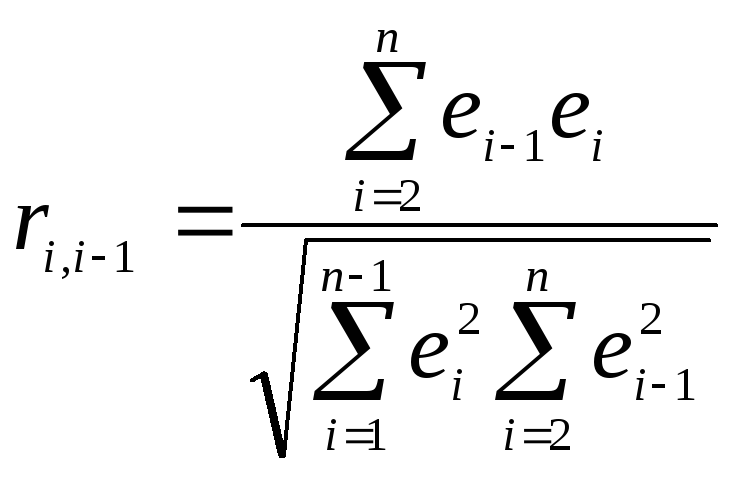
Связь выражается формулой: .

Значения r изменяются от –1 (в случае отрицательной автокорреляции) до +1 (в случае положительной автокорреляции). Близость r к нулю свидетельствует об отсутствии автокорреляции.

При отсутствии таблиц критических значений DW можно использовать следующее «грубое» правило: при достаточном числе наблюдений (12-15), при 1-3 объясняющих переменных, если , то отклонения от линии регрессии можно считать взаимно независимыми.

Либо применить к данным уменьшающее автокорреляцию преобразование (например автокорреляционное преобразование или метод скользящих средних).

Существует несколько ограничений на применение критерия Дарбина-Уотсона.

1. Критерий DW применяется лишь для тех моделей, которые содержат свободный член.

2. Предполагается, что случайные отклонения определяются по итерационной схеме

,

называемой авторегрессионной схемой первого порядка AR(1). Здесь – случайный член.

3. Статистические данные должны иметь одинаковую периодичность (не должно быть пропусков в наблюдениях).

4. Критерий Дарбина – Уотсона не применим к авторегрессионным моделям, которые содержат в числе факторов также зависимую переменную с временным лагом (запаздыванием) в один период.

Для авторегрессионных моделей предлагается h – статистика Дарбина

,

где – оценка коэффициента автокорреляции первого порядка,D(c) – выборочная дисперсия коэффициента при лаговой переменной y_t-1, n – число наблюдений.

Обычно значение рассчитывается по формуле, аD(c) равна квадрату стандартной ошибки S_c оценки коэффициента с.