Модели оценки доходности финансовых активов. Выбор оптимального портфеля ценных бумаг

Модель оценки доходности финансовых активов (САРМ) описывает зависимость между рыночным риском и требуемой доходностью. САРМ базируется на допущениях идеального рынка, на добавлении к допустимому множеству портфелей безрискового актива. Линия рынка капитала отражает зависимость риск-доходность для эффективных портфелей, то есть для портфелей, сочетающих рисковые и безрисковые активы. Линия рынка ценных бумаг отражает зависимость риск-доходность для отдельных акций. Требуемая доходность любой акции равна безрисковой норме, сложенной с произведением премии за рыночный риск и b- коэффициента акции. Формула определения требуемой инвесторами доходности финансового инструмента имеет вид:

r = r_f + β×(r_m -r_f)

r_f – безрисковый уровень доходности (risk free);

r_m – среднерыночный уровень доходности.

Коэффициент регрессии βслужит количественным измерителем систематического риска, не поддающегося диверсификации. Ценная бумага, имеющаяβ-коэффициент, равный 1, копирует поведение рынка в целом. Если значение коэффициента выше 1, реакция ценной бумаги опережает изменение рынка как в одну, так и в другую сторону. Систематический риск такого финансового актива выше среднего. Менее рисковыми являются активы,β-коэффициенты которых ниже 1 (но выше 0). Концепцияβ-коэффициентов составляют основу модели оценки финансовых активов (Capital Assets Pricing Model, CAPM). При помощи этого показателя может быть рассчитана величина премии за риск, требуемой инвесторами по вложениям, имеющим систематический риск выше среднего.

При наличии только двух активов множество допустимых портфелей ценных бумаг — это прямая или дуга. Однако если бы мы увеличили число активов в портфеле, мы бы получили целую достижимую об­ласть (см. рис. ниже).

Ожидаемая

доходность портфеля K_p,%

Эффективная граница (BCDE)

Рис. Эффективная граница инвестиционных портфелей

Точки А, Н, G и Е представляют собой портфели, содержа­щие только один вид цен­ных бумаг. Все другие точки в области и на ее границах пред­ставляют собой портфели, состоящие из двух или более ценных бумаг.

На рис. граница области, заключенная между точками BCDE, определяет эффектив­ное множество портфелей ценных бумаг и называется эффективной границей. Портфели, расположенные слева от эффективного множества, недости­жимы. Портфели, расположенные справа от границы (внутренние), неэффективны, по­скольку в этом случае найдутся дру­гие портфели с тем же риском, но более высокой доход­ностью либо с той же доходностью, но меньшим риском. Например, портфели С и D являются более предпочтительными по критерию «риск-доходность», чем X.

Для того чтобы определить, какой портфель ценных бумаг выберет инвестор необходимо знать степень несклонности инвестора к риску, которая отражается в его критерии риск-доход­ность (см. рис. ниже).

Ожидаемая доходность портфеля K_p,%

К_М

К_p

k_RF

0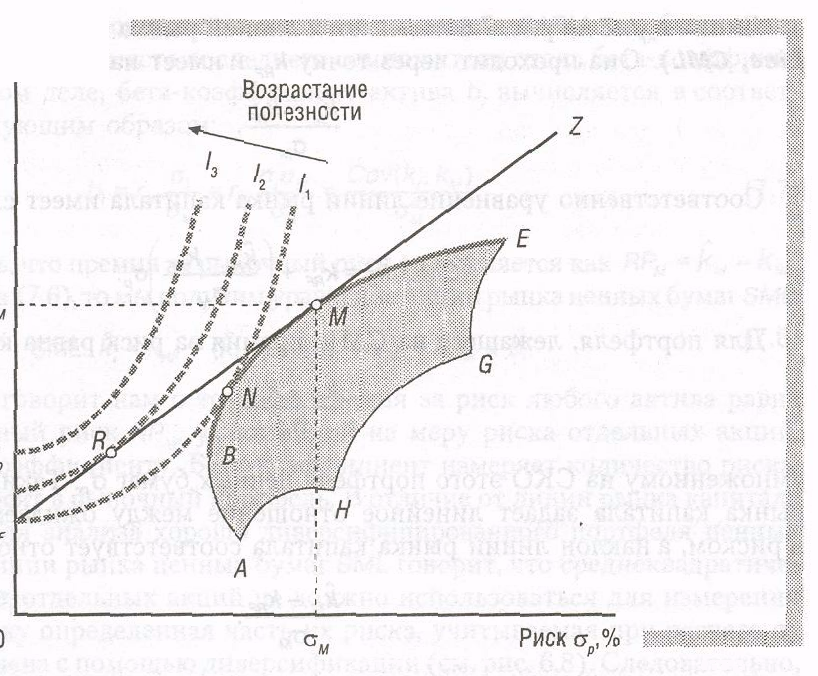

Рис. Выбор оптимального портфеля: учет рискованных и безрискового актива

Достижимое множество портфелей, состоящих из рискованных активов, это область AHGEMB. Кроме него изображено множество кривых безразличия (I₁,I₂,I₃) некоторого инвестора. Точка N, в которой кривая безразличияI₁, касается достижимого множества, пред­ставляет собой оптимальный выбор портфеля, со­стоящего только из рискованных активов.

Однако инвестор может построить и лучший портфель, чем N, — он может выйти на более высокую кривую безразличия. Используя безрисковый актив, он может добиться любого сочетания риска и доходности, соответствующего точке на прямой линии, соединяющей k_RFс М — точкой касания этой прямой, эффективной границы рискованных портфелей. Портфели, изображенные на линии k_RFMZ, оказываются более предпочтительными с точки зрения полезности инвесторов, чем портфели, состоящие исключительно из рискованных активов. Учитывая новые возможности, инвестор может теперь перейти из точки N в точку R, повысив, таким образом, свою полезность.

Если инвестор может, как занимать (продавать коротко), так и давать взаймы безрисковые и рискованные активы, то для него становится возможным выйти на отрезок прямой MZ.

Очевидно, что большинство инвесторов выберет портфели ценных бумаг, соответствующие различ­ным точкам на линии k_RFMZ. Таким образом, будут сформированы портфе­ли, пред­ставляющие сочетания безрискового актива и рискованного портфеля М. Отсюда можно заключить, что если рынок капитала находится в равновесии, то портфель М будет представлять собой рыночный портфель всех рискованных активов, присутствующих в эко­номике.

Сама по себе CAPM является изящной научной теорией, имеющей солидное математическое обоснование. Для того, чтобы она “работала” необходимо соблюдение таких заведомо нереалистических условий как наличие абсолютно эффективного рынка, отсутствие трансакционных издержек и налогов, равный доступ всех инвесторов к кредитным ресурсам и др. Тем не менее столь абстрактное логическое построение получило практически всеобщее признание в мире реальных финансов. Крупнейшие рыночные институты, такие как инвестиционный банк Merril Lynch, регулярно рассчитывают β-коэффициенты всех крупных компаний, котирующихся на фондовых биржах. Отсутствие в России сформированной финансовой инфраструктуры пока еще препятствует использованию всего потенциала, заложенного в данную модель.

В качестве альтернативы традиционной однофакторной модели САРМ можно назвать модель арбитражного ценообразования (Arbitrage Pricing Model, АРМ). В основе модели утверждение о том, что рисковая доходность определяется многими экономическими факторами (рыночная ситуация в стране, стабильность мировой экономики, инфляция, динамика процентных ставок и т.д.). Таким образом, модель должна включать множество факторов и в наиболее общем виде описывается зависимостью:

k_i = k_RF + (λ₁ - k_RF)b_i1 + … + (λ_j-k_RF)b_ij+ е_i

где λ_j – требуемая доходность портфеля с единичной чувствительностью кj-му экономическому фактору (b_j= 1) и нулевой чувствительностью (b_j= 0), к другим факторам;

е_i – влияние не включённых в модель специфических факторов на изменение доходностиi-й ценной бумаги;

b_ij– чувствительность доходностиi-го актива кj-му фактору.

Данная модель обладает достоинствами и недостатками. Основным недостатком является то, что она не предусматривает жёстких исходных предпосылок, которые свойственны модели САРМ, количество и состав релевантных факторов определяются аналитиком и заранее не регламентируются. Фактическая реализация модели связана с использованием сложного процесса математической статистики. Тем не менее, главное достоинство этой теории в том, что доходность является функцией многих переменных и рассматривается среди учёных как одна из перспективных.