Риск и доходность финансовых активов

Принимая инвестиционные решения, инвестор никогда не будет руководствоваться лишь соображениями ожидаемой доходности. Инвестор принимает решения после оценки рисковости инвестиций. Затем он определяет является ли уровень доходности достаточным для компенсации ожидаемого риска. Риском называется шанс неблагоприятного исхода, опасность, угроза потерь или повреждений. Под риском понимается возможность осуществления некоторого нежелательного события. Риск инвестиций связан с вероятностью того, что фактическая доходность окажется ниже ее ожидаемого значения: чем больше вероятность получить низкую доходность или убытки, тем более рисковыми являются инвестиции. Количественно риск измеряется как среднеквадратическое отклонение доходности актива, полученное по ретроспективным данным. Ожидаемая доходность инвестиций – это ожидаемое среднее значение распределения вероятностей возможных значений доходности. Общий вывод: чем выше риск, тем выше требуемая доходность на данный актив.

Вероятностные распределения и ожидаемый уровень доходности финансовых активов

В 1952 году Гарри Марковец разработал теорию управления инвестициями. Доходность рассматривалась как математические ожидание, а риск как дисперсия или стандартное отклонение от этой доходности. Для определения ожидаемой доходности по финансовым инвестициям рассчитывается математическое ожидание (К_i):

К_i= Р₁ k₁ + P₂k₂ + ...+ P_nk_n = ,

где k_i— один из возможных вариантов доходности акции (i– его номер);

Р_i— вероятность этого исхода, аn– общее число возможных исходов.

Риск по инвестициям измеряется путём вычисления дисперсии. Дисперсией называется мера разброса возможных исходов относительно ожидаемого значения: чем выше дисперсия, тем больше разброс. Для расчёта дисперсии используется следующая формула:

σ² = , где

Поскольку интерпретация «процент в квадрате» затруднительна, в качестве другого измерителя разброса значений часто используется среднеквадратическое отклонение (СКО(σ)), представляющее собой квадратный корень из дисперсии:

СКО = σ²

Для сравнения инвестиций с разной степенью риска и разной доходностью рассчитывается коэффициент вариации (CV):

CV = СКО / Ожидаемая доходность = σ / К_i

Коэффициент вариации отражает риск, приходящийся на единицу доход­ности.

Риск и доходность портфеля.

Рассмотрим теперь оценку рисковости активов, объединенных в портфель, в том числе и при различном их сочетании. Как будет показано ниже актив, входящий в портфель, обычно является менее рисковым, чем, если бы он был изолирован.

Ожидаемая доходность портфеля представляет собой взвешенную среднюю из показателей ожидаемой доходности отдельных ценных бумаг, входящих в данный портфель:

К_p = w₁K₁ + w₂K₂ + … + w_nK_n = , где:

K_i — ожидаемая доходность отдельных активов;

w_i— доля этих активов в портфеле изnценных бумаг (сумма значений w = 1).

n- количество ценных бумаг входящих в портфель.

Однако в отличие от доходов риск портфеля ценных бумаг (σ_p) будет ниже, чем средневзве­шенное значение отдельных активов. Бо­лее того, теоретически даже возможно построить портфель акций, которые по отдельности будут достаточно рискован­ными, однако портфель в целом окажется полностью лишенным риска:σ_P= 0

Расчет СКО портфеля производится, как и в случае расчета среднеквадратического отклонения одиночного актива, за исключением того, что портфель ценных бумаг рассматривается как единый актив, имеющий свою доходность. Если распределения доходностей ценных бумаг являются нормальными, то можно использовать следующее выра­жение для определения риска портфеля, состоящего из двух активов:

СКО портфеля А и В = σ_p=σ_A²+ (1 –w_A²)σ_B²+ 2w_A(1 –w_A)r_ABσ_Aσ_B,

где: w_A— это доля средств портфеля, инвестированная в актив А;

1 – w_A—доля портфеля, инвестированная в актив В.

Чтобы построить достижимое множество, потребуется коэффициент кор­реляции доходности этих активов (r_АВ). Рассмотрим три различных его значения: r_АВ= +1,0, r_AB= 0 и r_АВ= -1,0 и для каждого случая необходим рассчёт средней доходности К_p((К_p= w_Ak_A+ (1 – w_А)К_В)) и среднеквадратического отклонения доходности портфеля (σ_p):

Ожидаемая доходность К_p,%

Ожидаемая доходность К_p,%

Ожидаемая доходность К_p,%

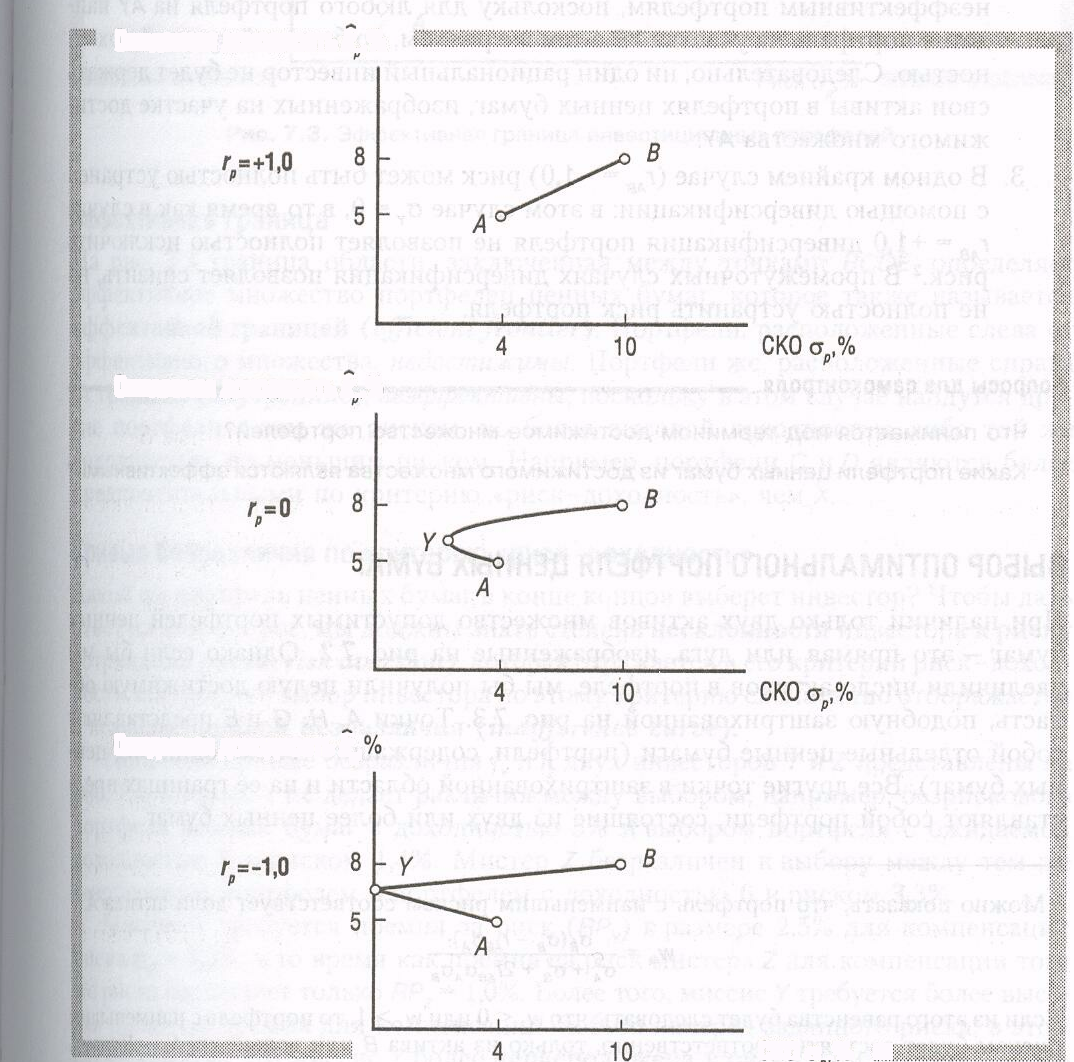
Рис. Построение достижимого множества портфелей из двух активов

В случае r_АВ= +1,0 все достижимые портфели оказываются эффективными, а в слу­чаях r_АВ= 0 и r_АВ= -1,0 эф­фективной будет лишь часть достижимого множе­ства от точки Y до В. Участок дуги от А до Y соответствует неэффективным портфелям, поскольку для любого портфеля на AY най­дется портфель на участке YB с тем же риском, но большей средней доход­ностью. Следова­тельно, ни один рациональный инвестор не будет держать свои активы в портфелях ценных бумаг, изображенных на участке дости­жимого множества AY.

В одном крайнем случае (r_AB= -1,0) риск может быть полностью устранен с помо­щью диверсификации: в этом случае σ_y= 0, в то время как в случаеr_AB= +1,0 диверсифи­кация портфеля не позволяет даже уменьшить риск. В промежуточных случаях дивер­сификация позволяет снизить, но не полностью устранить риск портфеля.