7.3. Нахождение оригинала по изображению

В общем случае нахождение оригинала по изображению достигается использованием теоремы обращения:

. (1)

Однако для произвольных это приводит к большим трудностям. Мы рассмотрим несколько удобных приемов нахожденияв предположении, чтоотношение двух многочленов, причем степень многочлена стоящего в знаменателе больше степени многочлена стоящего в числителе. Разложивна простейшие дроби, получим

,

где – комплексные числа, – нули знаменателя,– их порядок. Пользуясь формулой 10 таблицы соответствия и теоремой линейности, легко получить

и .

Часто бывает удобнее разложить изображение на простейшие дроби вида

, ,.

При этом также можно использовать формулы таблицы соответствия.

Пример 1. . Найти .

Решение. Разложим дробь на простейшие дроби:

,

.

Полагая , получим, при, получим, при, имеем.

.

Используя теорему линейности и таблицу соответствия (формулы 2,10), получим

.

При нахождении поиногда целесообразно использовать теорему о произведении изображений (теорему о свертке).

Пример 2. . Найти .

Решение

В некоторых случаях удобно использовать формулу Дюамеля.

Пример 3. 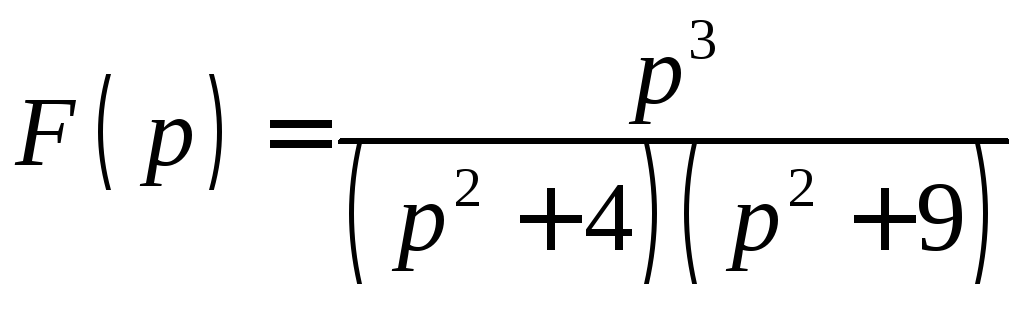. Найти .

Решение. ;

; .

По формуле Дюамеля имеем

Можно находить по, используя теорию вычетов (теорему разложения, которая выводится из (1)). А именно: еслиотношение двух многочленов, причем степень многочлена стоящего в знаменателе больше степени многочлена стоящего в числителе, то

(2)

где – полюса функции .

Пример 4. . Найти оригинал.

Решение. Функция имеет два полюса: – полюс второго порядка и– полюс первого порядка. По формуле (2)

.

Находим вычеты:

.

.

Если все полюса функциипервого порядка,то формулапринимает вид

,

где сумма берется по всем корням .

7.4. Решение линейных дифференциальных уравнений операционным методом

Пусть дано линейное дифференциальное уравнение

,

где ,,– постоянные коэффициенты и начальные условия: ,. Требуется найти решениеданного уравнения, удовлетворяющее начальным условиям. Будем считать, чторешение, а такжеи– оригиналы. Пусть,.

По теореме о дифференцировании оригинала имеем

, .

Применяя к обеим частям уравнения преобразование Лапласа, получим алгебраическое уравнение

, или

, .

Отсюда

.

Переходя от этого изображения к оригиналу, получим искомую функцию .

Пример 1. Найти частное решение дифференциального уравнения ,.

Решение. Пусть ;;

; .

Запишем операторное уравнение:

.

Откуда

.

Используя теорему линейности и таблицу соответствия формула (2), получим

.

Пример 2. Найти частное решение дифференциального уравнения ,,.

Решение. ; .

; ;

.

Используя таблицу соответствия формула (10) и теорему линейности, получим

.

Отметим особую роль формулы Дюамеля при решении линейных дифференциальных уравнений с постоянными коэффициентами. Пусть требуется решить линейное дифференциальное уравнение с постоянными коэффициентами

(3)

при нулевых начальных условиях. Если известно решение уравнения

(4)

с той же левой частью, а правой частью, равной 1, при нулевых начальных условиях, то формула Дюамеля позволяет записать решение данного уравнения без всяких вычислений. В самом деле пусть ,

Тогда операторные уравнения, соответствующие уравнениям (3), (4), имеют вид

, ,

откуда .

Тогда, согласно формуле Дюамеля,

или ,

или ,

или .

Пример 3. Найти решение дифференциального уравнения с нулевыми начальными условиями, ,.

.

Решение. Решаем сначала уравнение с теми же начальными условиями операционным методом:

, ; ; ;

;

разложим на простейшие дроби:

;

;

.

Используя теорему линейности и формулы соответствия, получим

, .

Применяя формулу Дюамеля, имеем