2.2. Аналитические функции

Понятие предела и производной для функции комплексного переменного вводятся так же, как и для функции действительного переменного.

Пусть функция определена в некоторой окрестности точкиСкажем, что существует пределесли существуют пределыи; при этом будем полагать

Если существует конечный предел

,

то этот предел называют производной функции в точкеи обозначаюта функциюназывают дифференцируемой в точке

Имеет место теорема: для того чтобы функция , определенная в области, была дифференцируема в точкеэтой области, необходимо и достаточно, чтобы функциии были дифференцируемы в той же точке (как функции двух переменных ) и чтобы, кроме того, в этой точке выполнялись условия Коши-Римана:

; .

При выполнении условий теоремы производная может быть представлена в одной из следующих форм:

Функция , дифференцируемая в каждой точке области , называется дифференцируемой в этой области, илианалитической.

Примеры

Функция является аналитической на всей комплексной плоскости. В самом деле, ;

Функция не является аналитической на комплексной плоскости. Действительно, здесь,,,,.

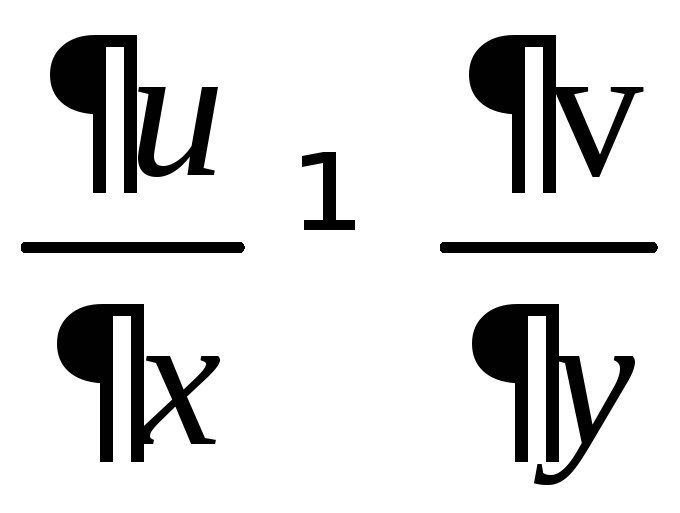Пользуясь условиями Коши-Римана, можно восстановить аналитическую функцию, если известна ее действительная часть или мнимая частьи, кроме того, задано значение функции в некоторой точке .

Пример. Восстановить аналитическую функцию , если дана ее действительная часть ,.

Решение. В силу условий Коши-Римана имеем

, (1)

. (2)

Интегрируя уравнение (2) по переменной , находим мнимую часть. Слагаемоеявляется постоянной (относительно) интегрирования. Дифференцируя последнее равенство по, и сравнивая результат с уравнением (1), получаем

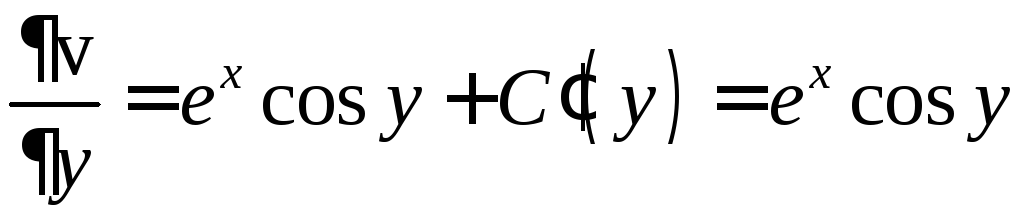, откуда

и .

Следовательно, и, то есть. Учитывая дополнительное условие, получим:, откуда. Итак,.

3. Интегрирование функций комплексного переменного

Пусть заданы функция комплексного переменного и кусочно-гладкая кривая . Последнее означает, чтоL состоит из конечного числа гладких дуг (дуг с непрерывно изменяющейся касательной). Если кривая L задана параметрическими уравнениями

(1)

где , то кривуюL будем всегда считать ориентированной в направлении возрастания параметра t.

Интеграл от функции можно определить через криволинейные интегралы от действительных функций и следующим образом:

. (2)

Пример 1. Вычислить интеграл , где– отрезок прямой, соединяющей точкии.

Решение. У нас ,,и, согласно (2), получим

.

Так как прямая проходит через точки икомплексной плоскости, то ее уравнение имеет вид,.

Поэтому окончательно находим

,

,

Таким образом, .

Если кривая задана параметрическими уравнениями

, где , то переменнаяпримет вид:

; .

В этом случае

. (3)

То есть для вычисления надо в подынтегральном выражении заменить накак под знаком функции, так и под знаком дифференциала и вычислить определенный интеграл в пределах отдо_.

Пример 2. Вычислить ,

где – отрезок параболы

Решение. По условию

.

Если кривая является окружностью с центром в точкеи радиусом, то(см. пример 1 из п.2.1). Запишем комплексное числов показательной формеДля всех точек окружностиоткуда следует, что, или,,. Тогда

. (4)

Формулы (2) – (4) используются чаще всего в том случае, если подынтегральная функция не является аналитической в области, содержащей кривую .

Если функция аналитическая в односвязной области, содержащей кривую , то

, где .

Пример 3. Вычислить интеграл , где– отрезок прямой, содержащей точкии.

Решение. Функция является аналитической на плоскости. Поэтому

.