Теорема аналитичности

Для всякого оригинала изображение определено в полуплоскости , где – показатель роста , и является в этой полуплоскости аналитической функцией. Если точкастремится к бесконечности так, чтонеограниченно возрастает, то стремится к нулю: .

Предельные соотношения

Если является оригиналом вместе со своей производнойи, то, гдевнутри угла, и; если существует, то .

Теорема линейности

Если иявляются оригиналами и,, то для любых комплексных постоянныхитакже является оригиналом и, то есть линейной комбинации оригиналов соответствует линейная комбинация изображений.

Теорема подобия

Если является оригиналом и, то для любого постоянногофункциятакже является оригиналом и, то есть умножение аргумента оригинала на положительное число приводит к делению аргумента изображения и самого изображения на то же число.

Теорема смещения

Если является оригиналом и, то для любого действительного или комплексного числатакже является оригиналом и, то есть умножение оригинала на функцию влечет за собой «смещение» независимой переменой .

Теорема запаздывания

Если является оригиналом и, то для любого постоянногофункциятакже является оригиналом и, то есть запаздывание оригинала на времясоответствует умножению изображения на.

Теорема о дифференцировании по параметру

Если при любом оригиналусоответствует изображение, то.

Теорема о дифференцировании оригинала

Если ,являются функциями-оригиналами и, то.

,

и, вообще,

,

где под понимается правое предельное значение.

Теорема о дифференцировании изображения

Если является оригиналом и, то, то есть дифференцирование изображения сводится к умножению оригинала на. Вообще,, где– натуральное число.

Интегрирование оригинала

Если является оригиналом и, то, то есть интегрирование оригинала в пределах отдоприводит к делению изображения на.

Интегрирование изображения

Если является оригиналом,исходится, то, то есть интегрирование изображения отдосоответствует делению оригинала на.

Умножение изображений

Если иявляются оригиналами,и, то выражению, называемому сверткой функцийи, соответствует произведение изображений, то есть.

Существенное значение имеет так называемые формулы Дюамеля:

.

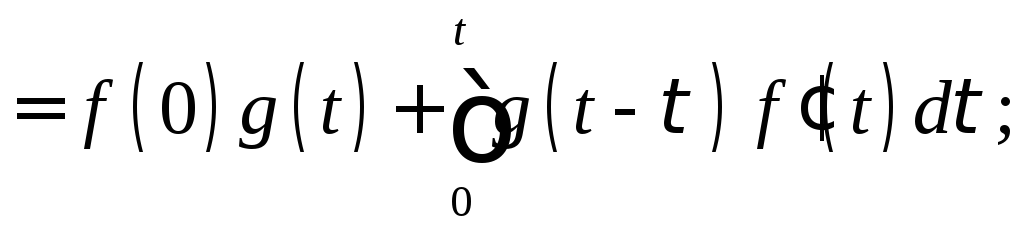
При нахождении изображений по оригиналам и оригиналов по изображениям, удобно пользоваться формулами соответствия, которые приведены в следующей таблице:

Номер формулы	Оригинал	Изображение
1	1
2
3
4
5
6
7
8
9
10
11

7.2. Нахождение изображения по оригиналу

Задачу о нахождении изображения по оригиналу можно решать, используя таблицу соответствия и свойства преобразования Лапласа.

Пример 1. . Найти.

Решение. Используя теорему линейности и формулы (1-4) таблицы соответствия, получим

.

Пример 2. . Найти .

Решение..

Используя теорему линейности, теорему затухания и формулу (8) таблицы соответствия, получим

.

Пример 3. . Найти.

Решение. .

Используя теорему об интегрировании изображения, находим

Пример 4. . Найти.

Решение. Используя теорему о дифференцировании изображения, находим

Если функция задана разными выражениями на разных промежутках, то ее надо предварительно представить в виде, где– функция Хэвисайда, а затем воспользоваться теоремой запаздывания.

Пример 5. Найти изображение функции

Решение. Представим в виде.

Имеем ; . Используя свойство линейности, получим .

Пример 6. Найти , если оригиналзадан графиком:

Решение

В аналитической форме

Заметим, что на интервале уравнение прямой найдено по формуле

.

Рассмотрим функции

Тогда (см. пример 5).

Поступая аналогично, получим