5. Изолированные особые точки

Точка называется изолированной особой точкой функции, еслианалитична в кольце, но не определена в точке

Если – изолированная особая точка функции, то эту функцию можно разложить в ряд Лорана (3), который сходится к ней в кольце, где– сколь угодно малое положительное число, а – расстояние от точки до другой особой точки функции.

Изолированная особая точка называется устранимой, если разложение (3) не содержит степеней разности с отрицательными показателями, то есть

.

Точка является устранимой особой точкой функциив том и только том случае, если функцияограничена в некоторой окрестности точки.

Пример 1. Функция имеет изолированную особую точкуЧтобы найти разложение в ряд Лоранав окрестности точки, воспользуемся формулой (5).

.

Это разложение не содержит степеней с отрицательными показателями. Следовательно, точка– устранимая особая точка.

Изолированная особая точка называется полюсом, если разложение (3) содержит конечное числостепеней разностис отрицательными показателями, при этом числоназывается порядком полюса.

Для определения порядка полюса функции можно использовать теорему.

Для того, чтобы точка являлась полюсом порядка функции , необходимо и достаточно, чтобы функциюможно было представить в виде

, (7)

где – аналитическая функция в окрестности точки и.

Полюса и нули аналитических функций связаны друг с другом.

Нулём функции называют любую точку, в которойРазлагая аналитическую функцию в ряд Тейлора (1) в окрестности нуля, получим:

, (8)

где иЧислоn называют порядком нуля аналитической функции в точке. Из (8) следует, что в окрестности нуля порядкаn аналитическая функция допускает представление

(9)

где . Кроме того, порядок нуля можно определить следующим образом.

Если , а, то порядок нуля аналитической функциив точкеравенn.

Справедливо утверждение.

Если аналитическую функцию можно представить в виде, где аналитические функциииимеют в точкенули порядкаk и m соответственно, и , и ,то в точкефункцияимеет полюс порядка, при; устранимую особую точку при.

В частности, если 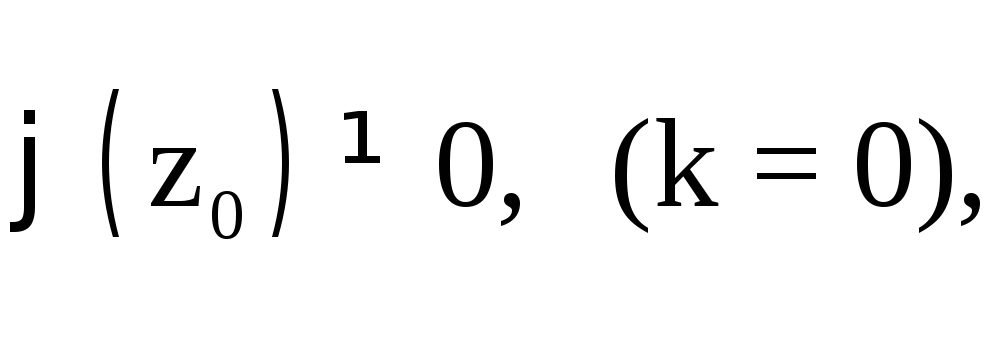аимеет в этой точке нуль порядкатоимеет в точкеполюс порядкаТо есть в этом случае порядок полюса функциисовпадает с порядком нуля знаменателя.

Изолированная особая точка называется существенно особой, если разложение (3) содержит бесконечное множество степенейс отрицательными показателями.

Пример 2. Найти все особые точки функций , определить их тип.

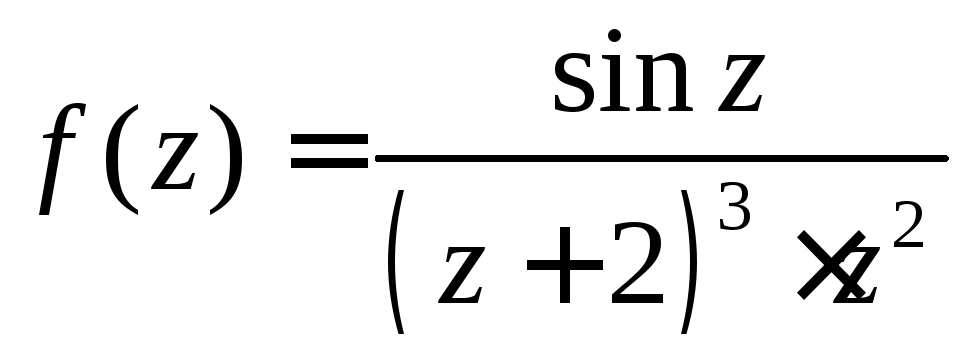1. . 2.. 3..

4.

Решение. 1. Чтобы найти разложение в ряд Лорана функции в окрестности точки, воспользуемся формулой (5). Получим:

,

Так как полученный ряд не содержит степеней с отрицательными показателями, то точкаявляется устранимой особой точкой.

2. Функция 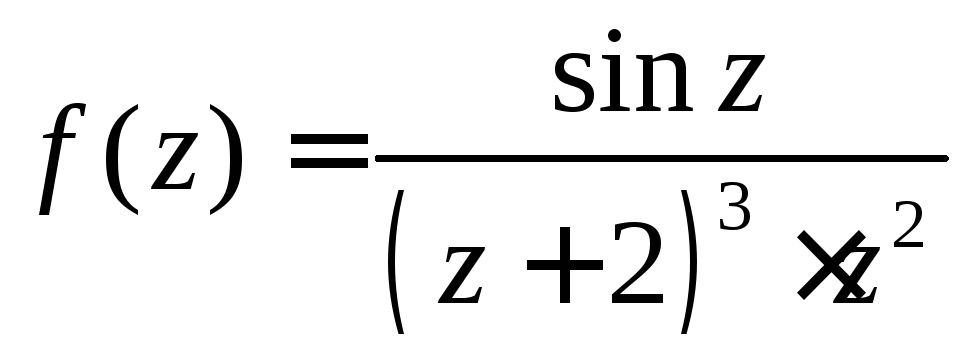имеет две изолированные особые точкии. Определим их тип. Пусть Представим функцию в виде, где, .

Тогда, согласно (7), есть полюс порядка.

Пусть Представим функцию в виде, гдеТак как при , то порядок нуля знаменателя .

Для имеем:, откуда следует, чтоимеет ноль первого порядка, то естьи.

Следовательно, точка есть полюс порядка , то есть простой полюс.

3. Функция имеет изолированную особую точкуПодставим в разложение в ряд Тейлора (5) функциивместоz выражение Получим разложениев окрестности особой точки

.

Этот ряд содержит бесконечное множество степеней с отрицательными показателями; следовательно,– существенно особая точка.

4. Для функции точки(k – целое число) являются нулями первого порядка, так как ,Тогда дляточкиявляются полюсами первого порядка (см. (7)), так как

Бесконечно удаленную точку называют изолированной особой точкой функции, если в некоторой ее окрестности (то есть вне круга с центром в точкедостаточно большого радиуса) нет других особых точек функции. Для изучения поведения функциив окрестности точкиполагают. Тогда окрестность точкиперейдет в окрестность точкии. Еслиявляется устранимой, полюсом или существенно особой точкой для функции, тосчитают, соответственно, устранимой, полюсом или существенно особой точкой функции.

Можно показать, что точка будет устранимой, полюсом или существенно особой точкой функции, если ряд Лорана дляв этой точки окрестности не содержит степенейс положительными показателями, содержит их в конечном числе или бесконечное множество соответственно.

Пример 3. Исследовать поведение функции в окрестности бесконечно удаленной точки.

Решение. Введем переменную . Тогда

.

Так как ограничена в окрестности точки,является устранимой особой точкой для, то и точкатакже является устранимой особой точкой для функции.

Пример 4. Исследовать поведение функции в окрестности бесконечно удаленной точки.

Решение. Разложим данную функцию в ряд Лорана. Для этого подставим в разложение в ряд Тейлора (5) функции вместоz выражение

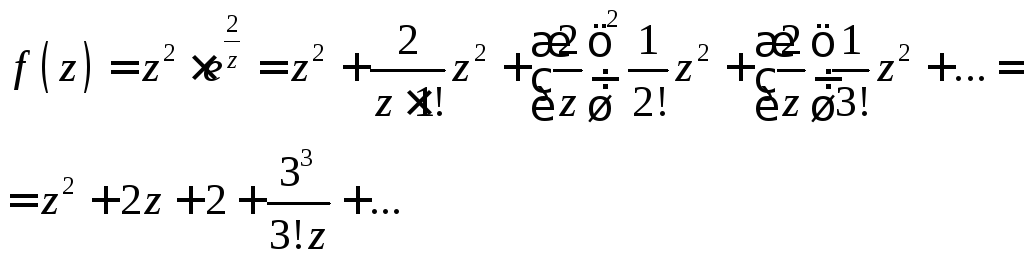
Это разложение содержит конечное число степеней с положительными показателями, причем наивысший показатель степени. Поэтому точкаявляется полюсом второго порядка для функции.