6. Вычеты и их применение к вычислению интегралов

6.1. Определение и вычисление вычетов

Пусть – область, границей которой является кривая. Скажем, что криваяориентирована в положительном направлении, если при движении точки вдоль нее в направлении ориентации областьостается слева.

Вычетом аналитической функции относительно изолированной особой точкиназывают число

.

Здесь – окружность радиуса, лежащая в области аналитичности функциии ориентированная в положительном направлении.

Если разложить в ряд Лорана в окрестности изолированной особой точки, то, где – коэффициент при в ее лорановском разложении.

Если – устранимая особая точка, то. Если – полюсI–го порядка, то

. (1)

При этом если и, , ,

(– полюсI–го порядка), то

. (2)

Формула (2) следует из равенства (1). Если – полюс порядка, то

. (3)

Пример 1. Найти вычеты функции относительно всех полюсов.

Решение. Данная функция имеет полюс I–го порядка и полюс порядкав точке. Воспользуемся формулой (1):

.

Используя формулу (3), получаем при :

Пример 2. Найти вычеты функции , где.

Решение. Функция имеет изолированную особую точку. Разложимв ряд Лорана в кольце, для чего используем разложение функциив ряд Тейлора

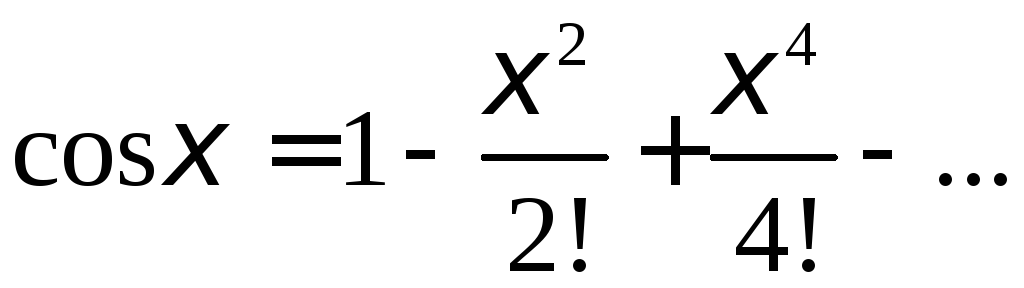и положим :

В силу единственности разложения в ряд Лорана, полученное разложение функции по степенямявляется рядом Лорана для данной функции в кольце. Так как этот ряд содержит бесконечное число степеней с отрицательными показателями, то точкаявляется существенно особой точкой, и

.

Пример 3. Найти вычеты функции , где.

Решение. Функция имеет изолированную особую точку. Разложимв ряд Лорана в кольце, для чего используем разложение функциив ряд Тейлора

и положим :

.

В силу единственности разложения в ряд Лорана, полученное разложение функции по степенямявляется рядом Лорана для данной функции в кольце. Так как этот ряд не содержит степеней с отрицательными показателями, то точкаявляется устранимой особой точкой. Следовательно,.

Пример 4. Найти вычеты функции , где

Решение. Функция имеет полюса первого порядка в точках(см. пример 2 §5). Воспользуемся формулой (2).

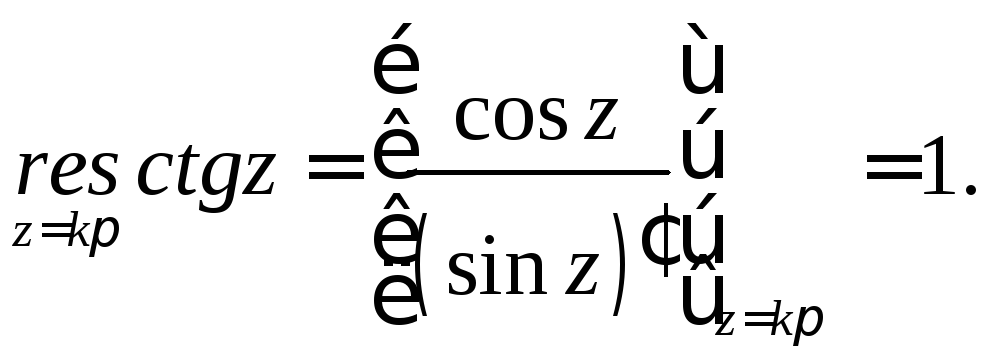
6.2. Применение вычетов к вычислению интегралов

Основная теорема Коши. Пусть – аналитическая функция в ограниченной односвязной области, за исключением конечного числа изолированных особых точек, и пусть замкнутая кривая, охватывающая эти особые точки, целиком лежит в области. Тогда если криваяориентирована в положительном направлении, то

.

Пример 1. Вычислить , где– окружность.

Решение. Подынтегральная функция имеет два полюсаI–го порядка и, которые расположены внутри круга. Согласно теореме Коши, получаем

.

Найдем вычеты:

,

.

Итак, .

Пример 2. Вычислить .

Решение. Подынтегральная функция имеет изолированную особую точкувнутри круга. Для определения характера изолированной особой точки разложим функциюв ряд Лорана в кольце. Воспользуемся разложением функциив ряд Тейлора:

и положим :

.

В силу единственности разложения в ряд Лорана, полученное разложение функции по степенямявляется рядом Лорана для данной функции в кольце. Так как главная часть этого ряда Лорана содержит бесконечное множество слагаемых, то точкаявляется существенно особой точкой.

Согласно теореме Коши получаем

.

Пример 3. Вычислить .

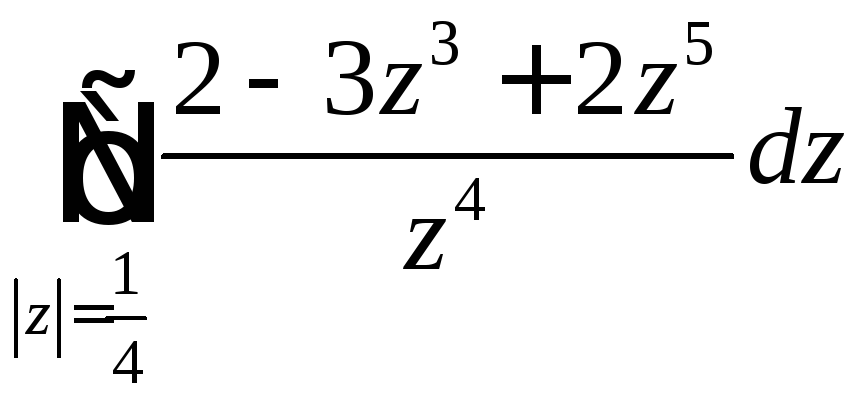Решение. Подынтегральная функция имеет изолированную особую точкувнутри круга. Так как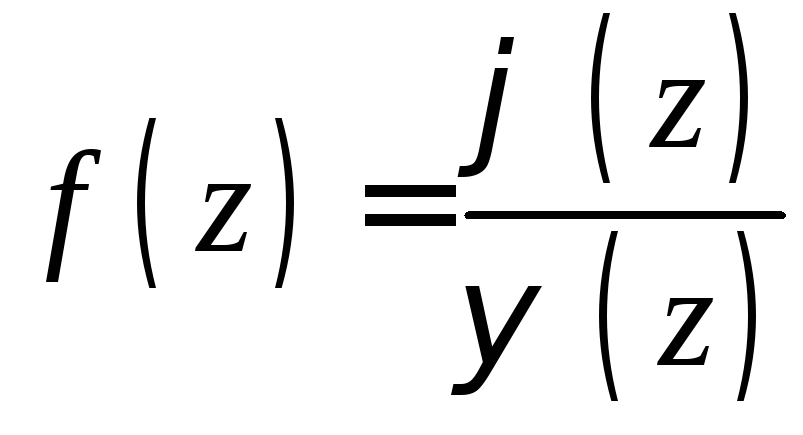, где, причем, а, тоесть полюс 4-го порядка.

Следовательно,

=

Согласно теореме Коши получаем

.

Пример 4. Вычислить .

Решение. Функция имеет полюсыI–го порядка в точках ,,. Точкинаходятся вне круга, так как>1,>1. Внутри круганаходится один полюспервого порядка. Найдемпо формуле (2), где,и,,. Имеем,.

Следовательно, по теореме Коши:

.