2. Функции комплексного переменного

2.1. Кривые и области на комплексной плоскости

Областью на комплексной плоскости называют множество точек, обладающее следующими свойствами:

вместе с каждой точкой из этому множеству принадлежит и достаточно малый круг с центром в этой точке (свойство открытости);

любые две точки можно соединить кривой, все точки которой принадлежат(свойство связности).

Приведем примеры кривых и областей на комплексной плоскости.

1. Где расположены точки , для которых, если– фиксированное комплексное число,?

Решение. Пусть ,.

Тогда

или .

Это уравнение окружности с центром в точке и радиусом.

2. Где расположены точки , для которых, если,?

Решение. Так как ,, то

.

После несложных преобразований получим , где,,.

Таким образом, данное равенство определяет прямую .

3. Построить линию .

Решение. Так как , то данное уравнение примет вид. Это прямая, проходящая через точкупараллельно оси.

4. Неравенство определяет верхнюю полуплоскость.

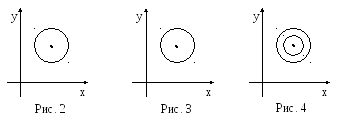
5. Неравенство определяет круг с центром в точкеи радиусом(рис.2).

6. Неравенство определяет круг с «проколотым» центром и радиусом(рис.3).

7. Неравенство определяет кольцо, ограниченное окружностями с центром в точке и радиусами и(рис.4).

8.Решить: а) систему уравнений; б), в) неравенства (геометрически):

а)

б) ;

в) .

Решение. а) Перепишем первое уравнение в виде . Множество решений этого уравнения задаёт окружность радиусом 1 с центром в точке(см. пример 1). Аналогично находим, что решением уравненияявляется окружность радиусом 1 с центром в точке (1+2i). Решением нашей системы уравнений являются точки пересечений этих окружностей.

Запишем z в алгебраической форме: z = x + yi.

Тогда

Отсюда, вычитая из первого уравнения второе, получим x = 3/2 . Подставив это значение в первое уравнение, найдём y:;,. Таким образом, решениями нашей системы являются числа,.

б) Представление z в алгебраической форме приводит нас к неравенству x  y. Решением этого неравенства является замкнутая полуплоскость (заштриховано).

в) Перепишем неравенство в виде

.

Решением этого неравенства является кольцо с центром в точке

(2, -3i), внутренний радиус которого равен 1, а внешний равен 2 (см. пример 7).

Область называется ограниченной, если существует кругтакой, что.

Ограниченная область называется односвязной, если любую замкнутую кривую, лежащую в , можно непрерывно деформировать в точку, оставаясь в области. Примером односвязной области является область на рис. 2. Области на рис. 3 и рис. 4 не являются односвязными.

Пусть в области комплексной плоскостиопределена комплекснозначная функция, то есть каждой точкепоставлено в соответствие комплексное число. Эту функцию можно представить в виде. Таким образом, комплекснозначную функцию комплексного переменного можно рассматривать как пару действительных функций двух действительных переменных, и многие свойства действительных функций естественным образом переносятся на функции комплексного переменного.

Примеры

Функция .

Здесь ,.

Функция . Здесь,.

–многочлен степени с комплексными коэффициентами.

Рациональная функция 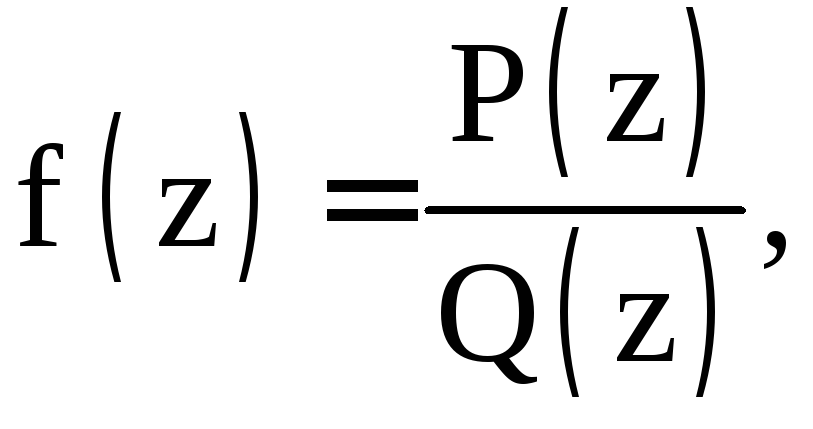гдеи– многочлены.

Учитывая формулы Эйлера, функции sin z и cos z для любого комплексного z определим равенствами

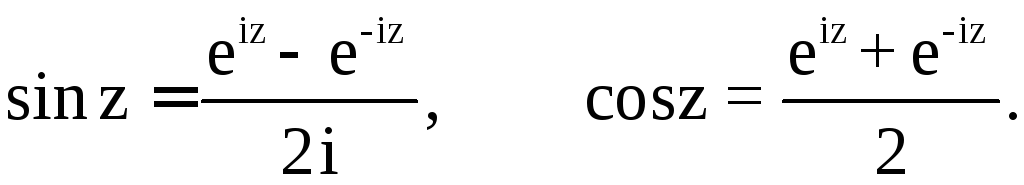
Отметим, что все формулы элементарной тригонометрии, справедливые для действительных x, остаются справедливыми и при всех комплексных значениях z. Кроме того, можно доказать, что уравнения иимеют решения только прито есть только на действительной оси. Следовательно, все решения уравнениянаходятся по формулеа все решения уравненияопределяются формулой

Функции tgz и ctg z для любого комплексного z определим формулами

Функции shz, chz и для любого комплексногоz определим равенствами

Из определения видно, что =Таким образом, свойства функцийинепосредственно вытекают из свойств функцийsinz, cosz и Отметим в частности, что все решения уравнениянаходятся по формулеа все решения уравненияопределяются формулой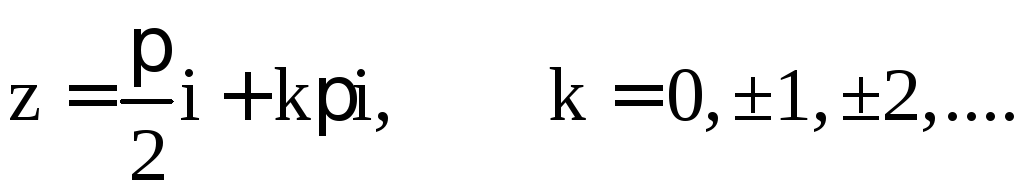. Кроме того, функцииинепрерывны на всей комплексной плоскости, а функциянепрерывна при, где