Интеграл вида

Теорема 1. Пусть , где и – многочлены степеней исоответственно. Еслинепрерывна на всей действительной оси и, то

,

где – полюса функциив верхней полуплоскости.

Пример 1. Вычислить .

Решение. Так как , тоудовлетворяет условию теоремы 1. Функцияимеет полюсвторого порядка в верхней полуплоскости. Поэтому, согласно теореме 1, находим

Интеграл вида

Интегралы вида , где – рациональная функция от, сводятся к интегралам по замкнутому контуру от функций комплексного переменного. Для этого выражаем синус и косинус по формулам Эйлера и делаем замену.

Имеем ,.

Подставляя эти выражения в подынтегральную функцию, получим – рациональную функцию. Логарифмируя

равенство , находими. При измененииот 0 доточкапробегает единичную окружностьв положительном направлении.

Следовательно, .

Последний интеграл по замкнутому контуру можно вычислить с помощью основной теоремы Коши.

Пример 2. Вычислить .

Решение. Пусть , тогда

, ,

, ; При измененииот 0 доточкапробегает единичную окружностьв положительном направлении.

Следовательно,

,

где .

Для нахождения полюсов найдем нули знаменателя и их порядки.– ноль первого порядка.

Так как тотакже нули первого порядка. Поскольку числитель функцииотличен от нуля в этих точках, то подынтегральная функция имеет три полюса первого порядка:

, ,

При этом ,

.

Итак, внутри единичной окружности находятся два полюса первого порядка:

и .

Найдем вычеты по формуле (2):

аналогично,

Итак, .

Интегралы вида ,

Теорема 2. Пусть 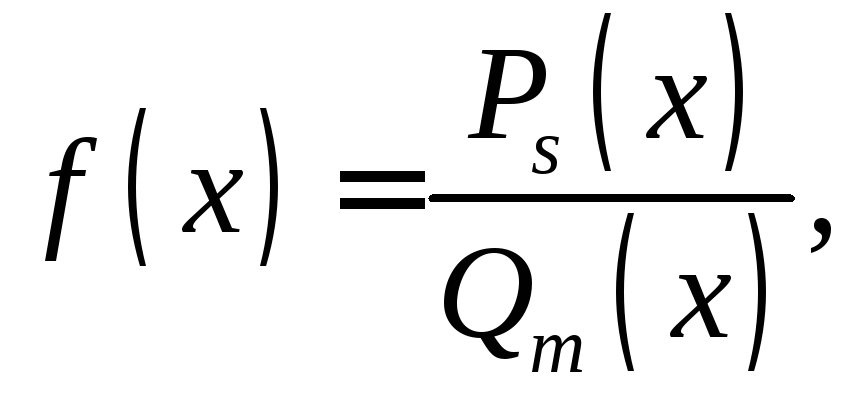гдеи– многочлены степенейисоответственно. Еслинепрерывна на всей действительной оси и, топри

,

,

где – полюса функциив верхней полуплоскости,.

Пример 1. Вычислить .

Решение. По условию, , значит. Функцияимеет полюс первого порядкав верхней полуплоскости. Поэтому на основании теоремы 2 и формулы (1) получаем

Пример 2. Вычислить .

Решение. По условию и.

Функция удовлетворяет условиям теоремы 2. Найдем полюсав верхней полуплоскости:

_, ,;

, ;

, ;

, ;

, .

Так как в точках, то– нули первого порядка функцииКроме тогоСледовательно функцияимеет полюсы первого порядка, в верхней полуплоскости. Поэтому на основании теоремы 2 и формулы (2)

,

где , .

Имеем:

.

Следовательно,

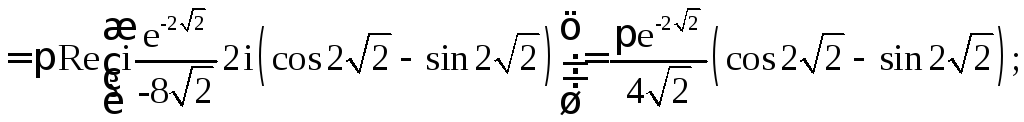
7. Преобразование Лапласа

7.1. Преобразование Лапласа и его свойства

Функцией – оригиналом будем называть любую комплекснозначную функцию действительного аргумента, удовлетворяющую следующим условиям:

непрерывна вместе со своими производными достаточно высокого порядка на всей оси , кроме отдельных точек, в которыхили ее производные терпят разрывI-го рода, причем на каждом конечном интервале оси таких точек имеется лишь конечное число;

для всех отрицательных ;

возрастает не быстрее показательной функции, то есть существуют такие постоянные ,, что для всех. Наименьшее число, для которого выполняется это неравенство, назовем показателем роста; для ограниченных оригиналов можно, очевидно, принять.

Простейшей функцией – оригиналом является так называемая единичная функция или функция Хэвисайда

Очевидно, умножение функции на «гасит» эту функцию для и оставляет без изменения для . Если функция удовлетворяет условиям 1 и 3 и не удовлетворяет условию 2, то произведение

будет удовлетворять и условию 2, то есть будет оригиналом (например, ,, и т.д.). Для простоты записи будем, как правило, опускать множитель , условившись, что все функции, которые будем рассматривать, равны нулю для всех отрицательных . Например, вместо будем писать 1, вместо – просто и так далее.

Изображением функции (по Лапласу) илипреобразованием Лапласа функции называют функцию комплексного переменного, определяемую соотношением. Связь оригинала и изображения будем записывать так:

.