11
При |
n=0 |
к |
(2.18) |
добавляется |
дополнительный |
вычет |
res0 [X ( z ) / z]z= 0 |
= |
limz→ 0 [X ( z )] в полюсе zp0 = 0, |
который дает множитель |
|||
1/z=zn-1|n=0. |
|
|
|
|
|
|
Существуют специальные таблицы обратных Z-преобразований для широкого класса дискретных функций [16].
Особенности вычисления обратного Z-преобразования при различных способах представления подынтегральной функции F(z) рассматриваются в п. 2.5.
Корни числителя Q(z) дробно-рациональной функции, описывающей сигнал X(z) (Q(z)=0), называются ее нулями. Отображение или представление нулей и полюсов на комплексной Z-плоскости используется в качестве геометрической интерпретации Z-образов дискретных сигналов.
2.4. ТЕСТОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ ДИСКРЕТНЫХ СИСТЕМ
Приводимые дискретные последовательности часто используются в системах ЦОС, в том числе в качестве их испытательных сигналов.
1. Единичный импульс: u0 ( n ) = { |
1, |
n= 0 |
. Имеет Z-образ U0(Z)=1 и |
0, |
n≠ 0 |
равномерный частотный спектр U0(jω )=1. Для дискретных систем он имеет такое же значение, как и дельта-импульс для аналоговых. Откликом на него является импульсная характеристика дискретной системы.
2 Единичный импульс, задержанный на m отсчетов:
u0 ( n − |
m ) = { |
1, n= m |
0, n≠ m . |
С учетом свойства задержки его Z и F (Фурье)-образы
Z{ u0 ( n − m )} = z− m ; F{ u0 ( n − m )} = e− jω mTд .
С помощью u0(n – m) любая дискретная последовательность может быть
представлена в виде дискретной свертки: |
x( n ) = ∑∞ |
x( m )u0 ( n − |
m ). |
|||
|
|
|
|
m= |
−∞ |
|
3. Единичный скачок: u1( n ) = { |
1, |
n≥ 0 |
(функция включения). Его Z-образ |
|||
0, |
n< 0 |
|||||
U1( z ) = ∑∞ |
z − n = 1/(1− z − 1 ) = z /(1− |
z ) |
соответствует сумме |
бесконечного |
||
n= 0 |
|
|
|
|
|
|
числа членов геометрической прогрессии. Сигнал имеет один полюс zp=1 и нуль z0=1 в начале координат (рис. 2.4, а).
Выражение для спектра единичного скачка находится следующим образом:
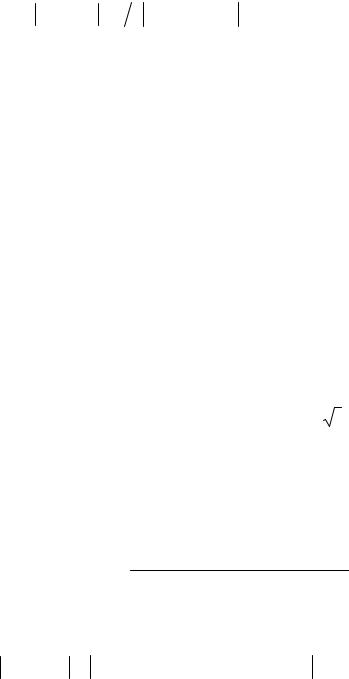
12
|
|
|
= 1 /(1 − e − jω Tд |
|
|
||||||||||
U1( jω ) = U1( z ) |
|
z= e |
jω T |
) = |
|
||||||||||
|
|
|
|
|
|
|
д |
|
|
|
|
|
|
||
= 1 / |
|
e |
− |
jω |
Tд / 2 |
jω |
Tд / 2 |
− e |
− |
jω |
Tд / 2 |
j(ω Tд− π |
) / 2 |
||
|
|
|
e |
|
|
|
|
= |
e |
/ [2 sin(ω Tд / 2)] |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(при выводе использована формула Эйлера: e± jα = cosα |
± j sinα ). |
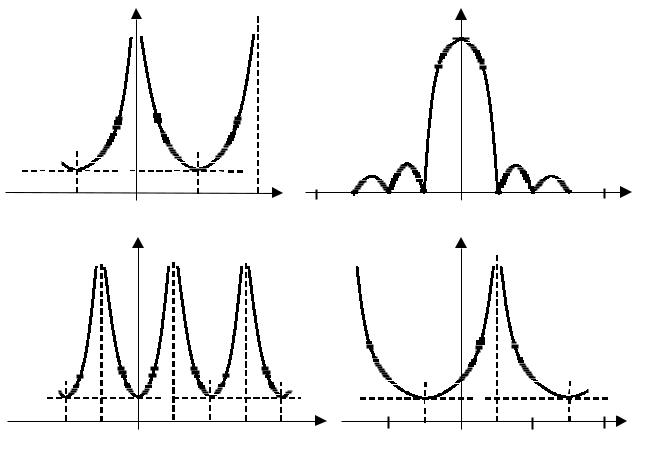
График модуля спектра U1( jω ) = 1 2 sin(ω Tд / 2 ) |
показан на рис. 2.5, а. |
Откликом на сигнал u1(n) является переходная характеристика дискретной системы.
4. Прямоугольный импульс конечной длительности:
uN ( n ) = 1, 0 ≤ |
n ≤ N − 1, |
uN ( n ) = |
0 |
для других n. |
|
|
|
|
|
||||||
|
|
|
N − 1 |
|
|
z − N ) /(1− |
z− 1 ) |
|
|
|
|
|
|
||
Его Z-образ |
U N ( z ) = ∑ z − n = |
(1− |
равен |
сумме конечного |
|||||||||||
|
|
|
n= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
числа |
членов |
геометрической |
|
прогрессии, |
определяемой |
как |
|||||||||
N − 1 |
a N ) /(1− a ) . |
|
|
|
|
|
|
|
|
|
|
|
|
||
S = ∑ |
ai = (1− |
К |
этому |
же |
результату |
можно |
прийти, |
||||||||
i= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
представив сигнал uN (n) в виде uN (n) = u1 (n) – u1 (n – N), |
что в Z-области |
||||||||||||||
означает: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U N ( z ) = U1( z ) − z− NU1( z ) = (1− z− N ) /(1− z− 1 ). |
|
|
|
|
|
|
|
|
|||||||
Сигнал имеет один полюс zp=1 и N нулей: ( 1 − |
z− N ) = 0 , |
zoi |
= |
N 1 = |
e j2π i / N , |
||||||||||
i = 0, |
1,…N |
– |
1, равномерно |
размещенных |
на |
единичной |
окружности |
||||||||
(рис. 2.4, б).
Спектр импульса определяется выражением
U N (jù ) = (1− e− jω NTд )/ (1−
= e− jω ( N − 1 )Tд / 2
|
− jω T |
e− jω NTд / 2 (e jω NTд / 2 − e− jω NTд / 2 ) |
|
e |
д )= |
e− jω Tд / 2 (e jω Tд / 2 − e− jω Tд / 2 ) |
= |
sin(ω NTд / 2 ) / sin(ω Tд / 2 ).
График модуля спектра U N ( jω ) = sin(ω NTд / 2 ) / sin(ω Tд / 2 ) показан на
рис. 2.5, б. Он соответствует дискретной функции sinc и имеет следующие значения в характерных точках:
13
|
U N ( jω |
) |
|
= |
|
N , |
ω |
= |
0 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
0, ω = 2π i / NTд = |
iω |
|
/ N , i = 1,2,...N − 1. |
|
|
||||||||||||
|
|
|
|
|
|
|
д |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
а) |
|
|
|
jb |
|
|
|
|
|
б) |
Z02 |
|
jb |
Z01 |
||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Z0 |
|
|
|
|
|
Zp a |
|
|
|
|
|
|
|
|
2π /N |
Zp a |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
-1 |
|
|
0 |
|
1 |
|
|
-1 |
|
|
|
0 |
|
|
|
|
1 Z00 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z0(N-1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) |
jb |
|
г) |
|
jb |
|
Zp |
|
|
|
Zp1 |
|
|
|
|
ω c |
|
|
ω |
c |
|
|
|
|
|
|
ω cTд |
||
|
|
|
|
|
|
Z0 |
ω cTд |
|
a |
Z01 |
a |
-1 |
0 |
1 |
-1 |
0 |
Z02 1 |
|
|
|
|
|
Zp2 |
Рис. 2.4. Картины нулей и полюсов для дискретных сигналов типа единичный скачок (а), импульс конечной длительности (б), комплексный (в) и вещественный (г) радиоскачок
Сигнал 4 применяется для анализа переходных процессов в апериодических дискретных системах.
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
а) |
|U1(jω )| |
|
|
б) |
|
|
|
|UN(jω )| |
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1/2 |
|
|
ω |
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
||
|
-ω д/2 |
0 |
ω д/2 |
ω д |
|
-ω д/2 |
-2ω д/N -ω д/N 0 ω д/N 2ω д/N |
ω д/2 |
||||
|
г) |
|X(jω )| |
|
|
в) |
|
|
|
|X(jω )| |
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1/2 |
|
|
ω |
|
|
|
1/2 |
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
-ω д/2 -ω c |
0 |
ω c ω д/2 |
ω д |
|
-ω д/2 -ω c |
0 |
ω c ω д/2 ω д-ω c ω д |
||||
Рис. 2.5. Графики модулей спектров дискретных сигналов типа единичный |
||||||||||||
скачок (а), импульс конечной длительности (б), комплексный (в) и |
|
|||||||||||
|
|
|
вещественный (г) радиоскачок |
|
|
|
||||||
5. |
Комплексный радиоскачок с частотой заполнения ω c |
: |
|
|||||||||
|
|
x( n ) = |
e jω cnTд = |
cos(ω |
c |
nT ) + |
j sin(ω |
c |
nT ), |
n ≥ |
0; |
|
|
|
|
|
|
д |
|
д |
|
|
|
||
Z-образ его, как и вещественного скачка, определяется суммой бесконечного числа членов геометрической прогрессии:
X ( z ) = ∑∞ |
e jω cnTд z − n = 1/(1− e jω cTд z − 1 ). |
|||||
|
n= |
0 |
|
|
|
|
СИГНАЛ ИМЕЕТ ОДИН НУЛЬ Z0 = 0 И ОДИН КОМПЛЕКСНЫЙ ПОЛЮС |
||||||
z p = e jω cTд НА ЧАСТОТЕ |
ω C (РИС. 2.4, В). СПЕКТР СИГНАЛА |
|||||
ОПИСЫВАЕТСЯ ВЫРАЖЕНИЕМ |
||||||
X ( jω ) = X ( z )| |
jω T = 1/(1− |
e jω сTд e− jùTд ) = |
||||
|
|
z= e |
д |
|
|
|
|
|
|
|
|
|
|
= e |
j[( ω − ω |
с )Tд− π ] / 2 |
/( 2 sin |
ω − ω c |
Tд ). |
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
15
Модуль его | X ( jω )| = 1/ 2 | sin(ω |
|
− ω c )Tд |
/ 2 | для ω |
c=ω |
д/4 показан |
|
|
|
||||||||||||||||||||||||
на рис. 2.5, в. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6. Вещественный радиоскачок с частотой заполнения ω |
c: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
x( n ) = cos(ω c nTд ) = |
( e jω сnTд + |
|
e− jω |
сnTд ) / 2, |
n ≥ 0. |
|
|
|
|
|
|
||||||||||||||||||
Его Z- преобразование |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos(ω cTд )z− |
1 |
|
|
|
|
|
|||||||||||
|
|
|
1/ 2 |
|
|
|
|
|
1/ 2 |
|
|
|
|
|
1− |
|
|
|
|
|
||||||||||||
X ( z ) = |
|
|
+ |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1− e− jω cTд z− 1 |
1− |
e jω |
|
сTд z− 1 |
1− |
2cos(ω |
cTд )z − 1 + |
z− |
2 |
|
|
|
||||||||||||||||||||
имеет пару комплексно-сопряженных полюсов z p1,2 = |
e |
± jω сTд |
|
и |
|
|
|
пару |
||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
нулей z01 = |
|
0 и z02 = cos(ω cTд ) (рис. 2.4, г). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
СПЕКТР СИГНАЛА X ( jω |
) = X ( z )|z= e jω Tд = |
|
|
|
|
1− |
|
cos(ω cTд )e− jω |
Tд |
|
, |
|||||||||||||||||||||
1− |
2cos(ω |
cTд )e |
− |
jω |
T |
e |
− j2ω T |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д + |
|
д |
|||||||||||||
взятый по модулю, показан на рис. 2.5, г для ω |
|
c=ω д/4. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Сигналы 5,6 используются для анализа переходных процессов и |
||||||||||||||||||||||||||||||||
избирательности селективных дискретных систем. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
7. Комплексный радиоимпульс конечной длительности NTД: |
|
|
|
|
|
|
||||||||||||||||||||||||||
x( n ) = |
e jω onTд = cos(ω |
0 nTд ) + |
j sin(ω 0 nTд ), |
0 ≤ |
n ≤ |
N − |
1. |
|
|
|
|
|
|
|||||||||||||||||||
Ему соответствует Z-образ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
N |
− 1 jω |
nT |
|
|
|
|
|
N /(1− e |
jω |
|
|
T |
− 1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
X ( z ) = ∑ |
|
e |
o д z− n = (1− e jω oNTд z− |
|
|
o |
д z |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
n= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и Фурье-преобразование |
|
|
|
|
|
|
|
|
|
|
|
ω |
− |
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
e− j( ω − ω o )NTд ) |
|
|
|
ω |
− ω |
|
|
|
sin |
o |
|
NTд |
|
|
|
|
|
|
|
|
|
||||||||
|
|
(1− |
|
− j |
|
o |
( N − 1)Tд |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
X ( jω ) = |
|
|
|
|
|
= e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||
|
(1− |
e− j( ω − ω o )Tд ) |
|
|
|
|
|
sin |
ω |
− |
ω |
o |
Tд |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Спектр комплексного радиоимпульса и его график соответствуют спектру видеоимпульса 4, смещенному на частоту ω О (влево или вправо в зависимости от знака частоты ω О).
8. Вещественный радиоимпульс конечной длительности NTД: x( n ) = cos(ω o nTд ), 0 ≤ n ≤ N − 1.