
- •А.С. Бадаев а.В. Чернышов
- •1. Микроэллектронные структуры и их строение
- •1.1. Виды химической связи
- •1.2. Основные свойства материалов, определяемые особенностями химических связей.
- •1.3.1. Кристаллические тела
- •1.3.3. Структура аморфных твердых тел
- •1.3.4. Структура тонких металлических пленок
- •1.3.5. Перспективные углеродные структуры
- •1.3.6. Проблема атомных радиусов
- •2. Механические свойства твердых тел
- •2.1. Деформация и механическое напряжение. Закон Гука.
- •2.2. Пластическая деформация кристаллов
- •2.3. Прочность и разрушение твердых тел
- •3. Тепловые свойства твердых тел
- •3.1. Нормальные колебания кристаллической решетки
- •3.1.1. Колебания в одномерной решетке
- •3.1.2. Колебания трехмерной кристаллической решетки
- •3.1.3. Энергия нормальных колебаний. Фононы
- •3.2. Теплоемкость твердого тела
- •3.3. Тепловое расширение твердых тел
- •3.4. Теплопроводность твердых тел
- •3.5. Диффузия в твердых телах
- •4. Основы зонной теории твердых тел
- •4.1. Волновые свойства электронов
- •4.2. Энергетические уровни электрона в изолированном атоме
- •4.3. Энергетический спектр электронов в кристалле
- •4.4. Эффективная масса электрона
- •4.5. Заполнение зон электронами у металлов, диэлектриков и полупроводников
- •5. Физические свойства диэлектриков
- •5.1. Диэлектрическая проницаемость и виды поляризации диэлектриков
- •5.2. Электропроводность диэлектриков
- •5.3. Диэлектрические потери
- •5.4. Электрическая прочность
- •5.5. Сегнетоэлектрики
- •5.6. Пьезоэлектрики
- •5.7. Электреты
- •6. Магнитные свойства твердых тел
- •6.1. Классификация твердых тел по магнитным свойствам
- •6.2. Природа ферромагнитизма
- •6.3. Процессы при намагничивании ферромагнетиков
- •6.4. Поведение ферромагнетиков в переменных магнитных полях
- •6.5. Ферриты
- •6.6. Тонкие магнитные пленки
- •6.7. Магнитный резонанс
- •Часть I
- •394026 Воронеж, Московский просп., 14
4.4. Эффективная масса электрона
Согласно формуле де Бройля, импульс свободного электрона связан с его волновым вектором k следующим соотношением:
![]() ,
,
а скорость поступательного движения электрона
![]() (4.38)
(4.38)
Дифференцируя (4.25) по k, получим
![]() .
.
Подставляя это в (4.23) и (4.38), найдем:
![]() ,
,![]() . (4.39)
. (4.39)
В таком виде выражения для импульса и скорости поступательного движения оказывают справедливыми не только для свободных электронов, но и для электронов, движущихся в периодическом поле кристалла. Импульс р в этом случае называют квазиимпульсом электрона.
Создадим в кристалле внешнее поле Е. Это поле действует на электрон с силой
![]() ,
,
сообщая ему ускорение
![]() .
.
За время dt сила F производит работу
![]() .
.
Эта
работа идет на приращение энергии
электрона
dE:![]() .
.
Отсюда
находим
![]() .
Подставляя это в правую часть выражения
дляа,
получим
.
Подставляя это в правую часть выражения
дляа,
получим
![]() . (4.40)
. (4.40)
Выражение (4.40) является аналогом второго закона Ньютона, вследствие чего величина
![]() , (4.41)
, (4.41)
имеющая размерность массы получила название эффективной массы электрона.
Эффективная масса не является массой в обычном понимании. Это понятие удобно для описания движения электрона в внешнем поле так, как описывается движение свободного электрона. Эффективная масса может быть как положительной, так и отрицательной: по абсолютному значению она может быть как во много раз больше, так и во много раз меньше массы m покоя электрона. Кроме того meэф в кристалле может изменяться с изменением его волнового вектора (рис.4.9).
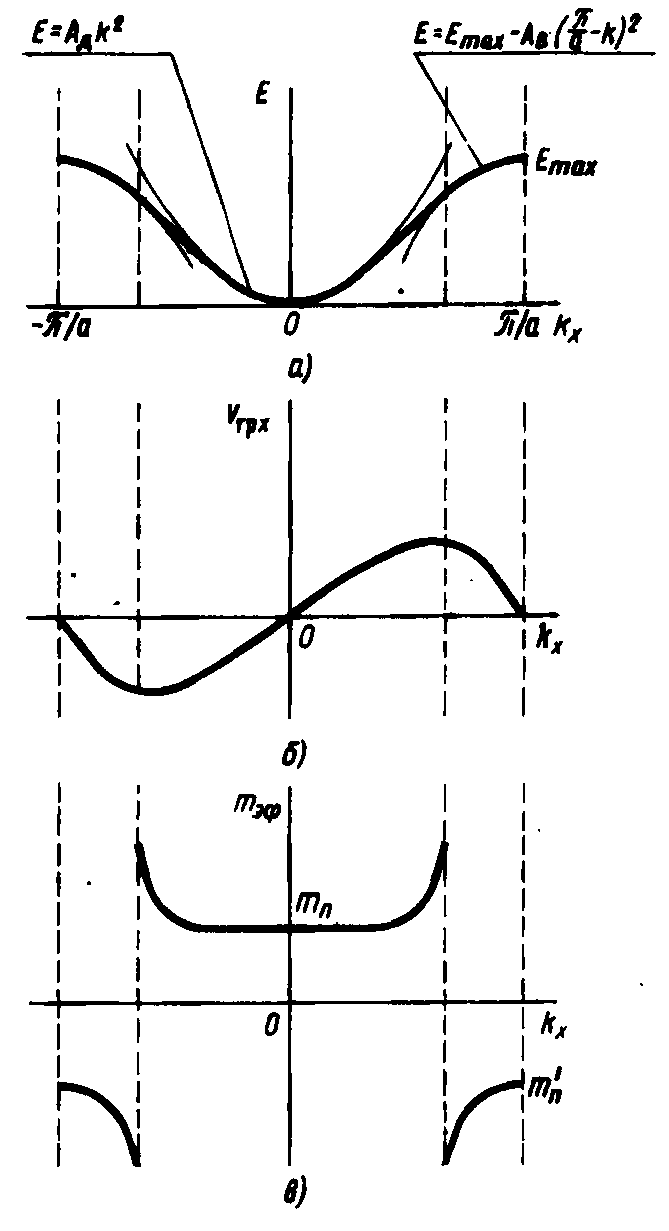
Рис. 4.9. Зависимость энергии (а), скорости (б) и эффективной массы (в) электрона от волнового вектора
Для
электронов, располагающихся у дна зоны,
энергия
![]() ,
вторая
производная от нее по k
равна
,
вторая
производная от нее по k
равна
![]() .
Подставляя
это в (4.41), получим следующее выражение
для эффективной массы электрона:
.
Подставляя
это в (4.41), получим следующее выражение
для эффективной массы электрона:
![]() . (4.42)
. (4.42)
Так как АД>0, то mn>0. Таким образом, электроны, располагающиеся у дна энергетической зоны, обладают положительной эффективной массой. Поэтому во внешнем поле, созданном в кристалле, они ведут себя нормально, ускоряясь в направлении действующей силы. Отличие таких электронов от свободных состоит в том, что их эффективная масса может значительно отличаться от массы покоя. Из (4.42) видно, что чем больше АД, т. е. чем шире разрешенная зона, тем меньше эффективная масса электронов, располагающихся у дна этой зоны.
Для
электронов, находящихся у вершины зоны,
энергия
![]() ,
вторая
производная от Е
по
k
равна
d2E/dk2=-2Ава2
и
эффективная масса
,
вторая
производная от Е
по
k
равна
d2E/dk2=-2Ава2
и
эффективная масса
![]() . (4.43)
. (4.43)
Она
является величиной отрицательной. Такие
электроны ведут себя во внешнем поле,
созданном в кристалле, аномально: они
ускоряются в направлении, противоположном
действию внешней силы. Абсолютная
величина ![]() ,
и
в этом случае определяется шириной
энергетической зоны: чем шире зона, тем
меньше
,
и
в этом случае определяется шириной
энергетической зоны: чем шире зона, тем
меньше ![]() .
.
Выясним теперь, чем обусловлено столь «странное» поведение электрона в кристалле.
Для свободного электрона вся работа А внешней силы F идет на увеличение кинетической энергии поступательного движения:
![]() .
.
Дифференцируя
Eк
дважды по k,
получим
d2Eк/dk2
=ћ2/m.
Подставляя
это в формулу (4.41), найдем тэф
=
т.
Таким
образом, эффективная масса свободного
электрона равна просто массе покоя.
Иначе может обстоять дело с электроном
в кристалле, где он обладает не только
кинетической, но и. потенциальной
энергией. При движении его под действием
внешней силы F
часть работы этой силы может перейти в
кинетическую энергию
![]() ,
другая
часть — в потенциальную энергию U,
так
что А
=
,
другая
часть — в потенциальную энергию U,
так
что А
=
![]() +U.
В
этом случае кинетическая энергия, а
следовательно, и скорость движения
электрона будут возрастать медленнее,
чем у свободного электрона. Электрон
становится как бы тяжелее,
двигаясь
под действием силы F
с меньшим ускорением, чем свободный
электрон.
+U.
В
этом случае кинетическая энергия, а
следовательно, и скорость движения
электрона будут возрастать медленнее,
чем у свободного электрона. Электрон
становится как бы тяжелее,
двигаясь
под действием силы F
с меньшим ускорением, чем свободный
электрон.
Если вся работа внешней силы будет переходить в потенциальную энергию U электрона, т. е. А =U, то приращения кинетической энергии и скорости движения электрона происходить не будет – электрон будет вести себя как частица с бесконечно большой эффективной массой.
Наконец,
если при движении электрона в потенциальную
энергию будет проходить не только вся
работа внешней силы F,
но и часть кинетической энергии
![]() ,
имевшейся у электрона, так что U=А+
,
имевшейся у электрона, так что U=А+![]() ,
то
по мере движения скорость такого
электрона в кристалле будет уменьшаться,
он будет замедляться, ведя себя как
частица, обладающая отрицательной
эффективной массой. Именно
так и ведут себя электроны, располагающиеся
у вершины энергетической зоны.
,
то
по мере движения скорость такого
электрона в кристалле будет уменьшаться,
он будет замедляться, ведя себя как
частица, обладающая отрицательной
эффективной массой. Именно
так и ведут себя электроны, располагающиеся
у вершины энергетической зоны.
Однако
в кристалле может реализоваться и
случай, когда при движении электрона
под действием внешней силы F
в кинетическую энергию переходит не
только вся работа внешней силы, но и
часть потенциальной энергии электрона
U',
так
что
![]() =А
+
U.
У
такого электрона
=А
+
U.
У
такого электрона
![]() и
скорость
и
скорость
![]() будут
расти быстрее, чем у свободного электрона.
Он становится как бы легче
свободного
электрона, обладая эффективной массой
тэф
<
т.
будут
расти быстрее, чем у свободного электрона.
Он становится как бы легче
свободного
электрона, обладая эффективной массой
тэф
<
т.
У
дна зоны (вблизи k
=
0), пока с увеличением k
энергия
Е(k)
электрона
растет примерно пропорционально k2,
скорость
поступательного движения электрона
![]() увеличивается
пропорционально k,
ускорение
движения положительно и эффективная
масса
увеличивается
пропорционально k,
ускорение
движения положительно и эффективная
масса
![]() сохраняет
постоянное положительное значение тn.
В
точке А
перегиба
кривой Е(k)
вторая
производная d2E/dk2=
0,
а первая производная dE/dk
достигает
максимума. Поэтому при приближении к
этой точке
сохраняет
постоянное положительное значение тn.
В
точке А
перегиба
кривой Е(k)
вторая
производная d2E/dk2=
0,
а первая производная dE/dk
достигает
максимума. Поэтому при приближении к
этой точке
![]() ,
а
,
а![]() .
За точкой перегиба dE/dk
начинает
убывать, поэтому убывает и
.
За точкой перегиба dE/dk
начинает
убывать, поэтому убывает и
![]() ;
ускорение
становится, таким образом, отрицательным,
что при сохранившемся направлении
действия внешней силы F
эквивалентно изменению знака эффективной
массы с положительного на отрицательный.
При этом может измениться и абсолютная
величина
;
ускорение
становится, таким образом, отрицательным,
что при сохранившемся направлении
действия внешней силы F
эквивалентно изменению знака эффективной
массы с положительного на отрицательный.
При этом может измениться и абсолютная
величина
![]() ,
еслименяется
кривизна кривой Е(k),
пропорциональная
d2E/dk2.
У
вершины зоны Е(k)
снова
становится квадратичной функцией k
и
эффективная масса достигает постоянного
отрицательного значения
,
еслименяется
кривизна кривой Е(k),
пропорциональная
d2E/dk2.
У
вершины зоны Е(k)
снова
становится квадратичной функцией k
и
эффективная масса достигает постоянного
отрицательного значения
![]()
