3.1.2. Колебания трехмерной кристаллической решетки

Рассмотрим теперь колебания в кристалле кубической формы с ребром L и объемом L³, грани которого параллельны граням элементарных ячеек.

Число стоячих волн в трехмерном кристалле объемом V, обладающих длиной, равной или большей λ, по аналогии с (3.5) должно быть равно

Более строгий расчет показывает, что

(3.6)

Так как , то

(3.7)

Дифференцируя это выражение, получим

(3.8)

Формула (3.8) выражает число нормальных колебаний, заключенное в интервале частот от ω до . Функция

(3 9)

определяет плотность заполнения спектрального участка dω) нормальными колебаниями, а следовательно, и частотный спектр этих колебаний. Функция g(ω) называется функцией распределения нормальных колебаний по частотам.

Так как общее число нормальных колебаний, которое может возникнуть в решетке, равно 3N, то g(ω) должно удовлетворять следующему условию нормировки:

, (3.10)

где ω_д – максимальная частота, ограничивающая спектр нормальных колебаний сверху.

Подставив (3.9) в (3.10) и проинтегрировав, получим

. (3.11)

Отсюда находим

(3.12)

Частота называется характеристической дебаевской частотой. Температура

(3.13)

(k - постоянная Больцмана) называется характеристической температурой Дебая.

При температуре Дебая в твердом теле возбуждается весь спектр нормальных колебаний, включая и колебание с максимальной частотой ω_д. Поэтому дальнейшее повышение температуры (выше ) не может уже вызывать появление новых нормальных колебаний. Действие температуры в этом случае сводится лишь к увеличению степени возбуждения каждого нормального колебания, приводящего к возрастанию их средней энергии.

Температуры Т > принято называть высокими. Подставив из (3.11) в (3.9), получим

(3.14)

Функция распределения нармальных колебаний (3.9) представлена на рис.3.3.

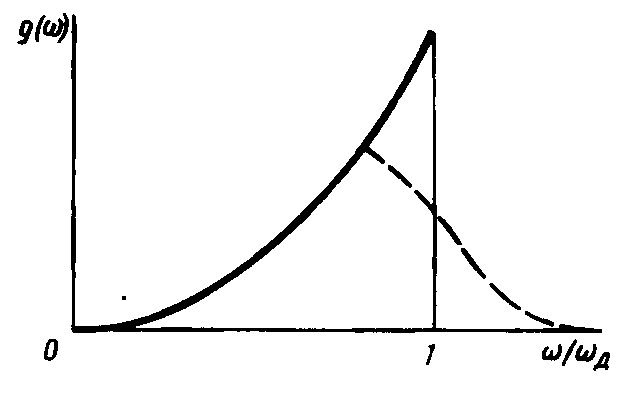
Рис. 3.3. Функция распределения нормальных колебаний по частоте

Частота нормальных колебаний в трехмерном кристалле зависит в общем случае не только от длины волны, но и от ее поляризации и направления распространения. Таким образом, вместо одной дисперсионной кривой для линейной цепочки атомов теперь для любого направления волны в кристалле существуют три дисперсионные кривые (рис. 3.4). В кубическом кристалле кривые для двух поперечных поляризаций совпадают, так что остается одна кривая для поперечных и другая – для продольных волн (более высокочастотных). Для решеток с базисом кроме акустических колебаний возникают также оптические колебания, соответствующие колебаниям друг относительно друга различных подрешеток.

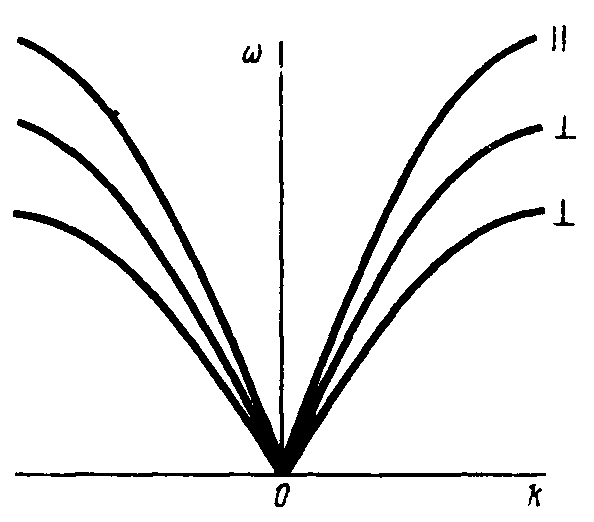
Рис. 3.4. Дисперсионные кривые для акустических колебаний в кристалле

3.1.3. Энергия нормальных колебаний. Фононы

С точки зрения классической теории энергия нормального колебания может быть любой и изменяться плавно на сколь угодно малые значения. Квантовая же механика утверждает, что энергия нормального колебания с частотой (ω_нк может принимать только дискретный ряд значений:

. (3.15)

где ћ – постоянная Планка, деленная на 2π.

Минимальная энергия нормального колебания не равна нулю, а равна ћω/2, колебания с такой энергией называются нулевыми.

Кроме того доказывается, что энергия решетки равна энергии нормального осциллятора, имеющего массу, равную массе колеблющихся атомов, и колеблющегося с частотой, равной частоте нормального колебания: .Полная энергия кристалла, в котором возбуждены все 3N нормальных колебаний, равна

.

Следует подчеркнуть, что нормальные осцилляторы не имеют ничего общего с реальными атомами, кроме одинаковой массы. Каждый осциллятор представляет одно из нормальных колебаний решетки, в котором участвуют все атомы кристалла, совершая его с одной и той же частотой ω.

На рис. 3.5 показан энергетический спектр линейного гармонического осциллятора. Он состоит из совокупности дискретных уровней, отстоящих друг от друга на расстоянии, равном ћω.

Минимальная энергия нормального колебания не равна нулю, а равна ћω/2, колебания с такой энергией называются нулевыми.

Так как , то энергия нормальных колебаний решетки должна определяться выражением 3.15), а их энергетический спектр должен совпадать со спектром, показанным на рис. 3.5.

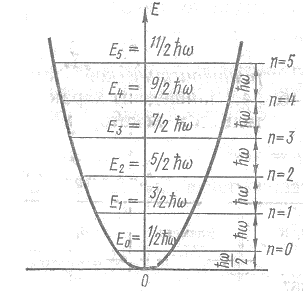
Рис. 3.5. Энергетический спектр линейного гармонического осциллятора

Минимальная порция энергии, которую может поглотить или испустить решетка при тепловых колебаниях, соответствует переходу возбуждаемого нормального колебания с данного энергетического уровня на близлежащий соседний уровень и равна

. (3.16)

Этот квант энергии тепловых колебаний решетки называется фононом.

Поле упругих волн, заполняющих кристалл, можно трактовать как газ, образованный квантами нормальных колебаний решетки – фононами, обладающими энергией и импульсом

, (3.17)

где υ – скорость звука, λ – длина упругой звуковой волны.

С этой точки зрения нагретый кристалл можно уподобить объему, заполненному фононным газом.

В кристаллической решетке могут возбуждаться нормальные колеьания с разными частотами, поэтому фононы могут обладать различными энергиями. Средняя энергия возбужденного нормального колебания с частотой ω:

. (3.18)